Boolean
Algebra & Digital Logic
Boolean
algebra was developed by the Englishman George Boole, who published the
basic principles in the 1854 treatise An
Investigation of the Laws of Thought on Which
to
Found the Mathematical Theories of Logic and Probabilities.
The
applicability to computing machines was discovered by three Americans
Claude Shannon Symbolic Analysis of
Relay and Switching Circuits, 1938.
George Stibitz An employee of Bell Labs, he developed
a binary adder
using
mechanical relays in 1937, the model “K 1” adder
because
he built it at home on his kitchen table.
John Atanasoff He was probably the first to use purely
electronic relays
(vacuum
tubes) to build a binary adder.
Boolean
algebra is a two–valued algebra based on the constant values denoted as either
FALSE, TRUE
0, 1
The
use of this algebra for computation is based on the fact that binary arithmetic
is based on two values, always
called “0” and “1”.
Basic
Boolean Operators
Boolean
algebra is defined in terms of two constants (defined above), which we
call “0” and “1”. Other courses will call these values “F” and
“T”.
Boolean
algebra is defined in terms of three basic operators, to which we shall add
a useful fourth operator. The three operators are NOT, AND, & OR.
Each
of these three basic operators is implemented by a basic electronic device
called a “logic gate”. We present the gates along with the
definition.
NOT This function takes one
input and produces one output. The gate
is shown
below. The circle at the right end of the triangle
is important.
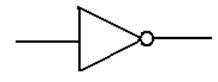
Algebraically,
this function is denoted f(X) = X’ or f(X) = ![]()
The
evaluation of the function is simple: ![]() = 1 and
= 1 and ![]() = 0.
= 0.
Basic
Boolean Operators (Part 2)
Logic OR
This
is a function of two Boolean variables.
We denote the logical OR of two Boolean
variables X and Y by “X + Y”. Some logic books will use “X Ú Y”.
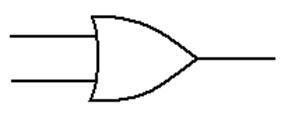
The
evaluation of the logical OR function is shown by a truth table
|
X |
Y |
X + Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Basic
Boolean Operators (Part 3)
Logic AND
This
is a function of two Boolean variables.
We denote the logical AND of two Boolean
variables X and Y by “X · Y”. Some logic books will use “X Ù Y”.
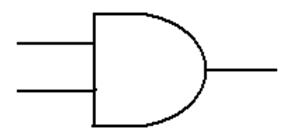
The
evaluation of the logical AND function is shown by a truth table
|
X |
Y |
X · Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Another
Boolean Operator
While
not a basic Boolean operator, the exclusive OR is very handy.
Logic XOR
This
is a function of two Boolean variables.
We denote the logical XOR of two Boolean
variables X and Y by “X Å Y”. Most logic books seem to
ignore this function.
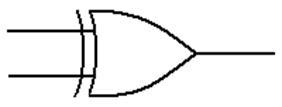
The
evaluation of the logical XOR function is shown by a truth table
|
X |
Y |
X Å Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
From
this last table, we see immediately that
X Å 0 = X and X Å 1 = ![]()
Time–Varying
Inputs and Outputs
Consider
the figure below, adapted from the text by Rob Williams. What does it tell us?
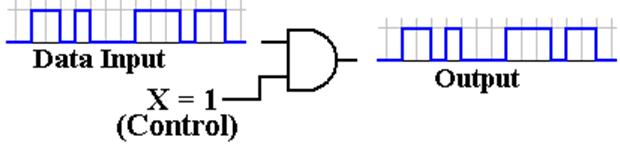
This
is a two–input AND gate, with inputs D (Data) and X (Control).
If X = 0, the output will be 0 independently of the value of the data input.
The
simple answer is that the gate output follows the input when X = 1.
The
input is a time sequence of values. At
any time, the data input to the AND
gate is either d = 0 or d = 1. At that
time, the output from the gate is either
Y = 0 or Y = 1.
The
use of the letter “O” as in “O = 1” is a bit hard to read; it appears confused.
More on the
Time Sequence
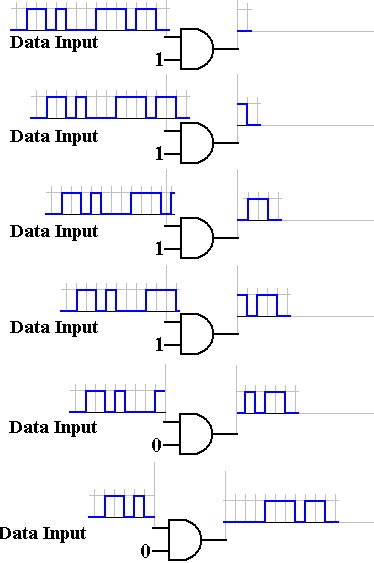
Truth Tables
The
fact that any Boolean variable can assume only one of two possibly values can
be shown, by induction, to imply the following.
For N > 0, N Boolean variables can take only 2N
different combinations of values.
For
small values of N, we can use this to specify a function using a truth table
with 2N
rows, plus a header row to label the variables and the function.
|
N |
2N |
|
1 |
2 |
|
2 |
4 |
|
3 |
8 |
|
4 |
16 |
|
5 |
32 |
|
6 |
64 |
Four–variable
truth tables have 17 rows total. This is
just manageable.
Five–variable truth tables have 33 rows total.
This is excessive.
N–variable truth tables, for N > 5, are almost useless.
Sample Truth
Table
|
A |
B |
C |
F1(A, B, C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
This truth table for 3
variables has 23 = 8 rows, plus a label row.
This
truth table forms a complete definition of the function. We shall later
give it another name, but can base
all our discussions on this table.
Another Sample
Truth Table
|
A |
B |
C |
F2(A, B, C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Two Truth
Tables in One
|
A |
B |
C |
F1(A, B, C) |
F2(A, B, C) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Truth tables are often used to
show pairs of functions, such as these two,
which will later be shown to be
related. This is easier than two
complete tables.
Truth tables rarely show more
than two functions, just because large truth
tables are “messy” and hard to
read.
Labeling
Rows in a Truth Table
The
row numbers are just labels. They are
not really a part of the truth table, but
aid in our discussions and conversions
to Boolean expressions.
The
row numbers are the decimal equivalents of the variable values viewed as binary
|
Row
Number |
X |
Y |
Z |
F(X,
Y, Z) |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
numbers.
The first row is always “row 0”.
0 = 0·4 + 0·2 + 0·1
1 = 0·4 + 0·2 + 1·1
2 = 0·4 + 1·2 + 0·1
3 = 0·4 + 1·2 + 1·1
4 = 1·4 + 0·2 + 0·1
5 = 1·4 + 0·2 + 1·1
6 = 1·4 + 1·2 + 0·1
7 = 1·4 + 1·2 + 1·1
Evaluation
of Boolean Expressions
The
relative precedence of the operators is:
1) NOT do this first
2) AND
3) OR do
this last
As
in the usual algebra, parentheses take precedence.
A·B + C·D, often written as AB + CD, is read as (A·B) + (C·D)
![]() is read as
is read as ![]() . The latter is really
messy.
. The latter is really
messy.
A·B + C·D = 1·0 + 1·1 = 0 + 1 = 1
A·(B + C)·D = 1·(0 + 1)·1 = 1 · 1 · 1 = 1
![]() =
= ![]() = 0 · 0 + 1 · 0 = 0 + 0 = 0
= 0 · 0 + 1 · 0 = 0 + 0 = 0
![]() =
= ![]() =
= ![]() = 1
= 1
![]() =
= ![]() = 0 · 1 = 0
= 0 · 1 = 0
The Basic
Unusual Boolean Theorem
Here
are two sets of theorems in Boolean algebra.
For all X 0·X = 0 OK
For all X 1·X = X OK
For all X 0 + X = X OK
For all X 1 + X = 1 What?
Consider
the following truth tables
|
W |
X |
W + X |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
From this, we derive the truth
table proving the last two theorems.
|
X |
0 + X |
1 + X |
|
0 |
0 |
1 |
|
1 |
1 |
1 |
Standard
Boolean Forms
In
this section, we develop the idea of standard forms of Boolean expressions.
In part, these forms are based on some standard Boolean simplification rules.
Standard
forms are either canonical forms or normal forms.
The
standard expressions are in either
SOP Sum of Products form, or
POS Product of Sums form.
This
lecture will focus on the following:
Canonical Sum of Products
Normal Sum of Products
Canonical Product of Sums
Normal Product of Sums
We
shall also discuss a few more variants that have no standard names.
IMPORTANT:
These forms use only the 3 basic Boolean
functions:
AND, OR,
NOT. Specifically, XOR is not used.
Variables
and Literals
We
start with the idea of a Boolean variable.
It is a simple variable that
can take one of only two values: 0 (False) or 1 (True).
Following
standard digital design practice, we use the values 0 and 1.
Following
standard teaching practice, we denote all Boolean variables by
single letters; normally “A”, “B”,
“C”, “D”, or “W”, “X”, “Y”, “Z”.
A
literal is either a Boolean variable or its complement.
Literals based on the variable X: X and ![]() .
.
Literals based on the variable Y: Y and ![]() .
.
NOTE: X and ![]() represent the same
variable,
represent the same
variable,
but they are not the same
literal.
X and ![]() represent different
variables.
represent different
variables.
Product and
Sum Terms
A
product term is the logical AND of
one or more literals,
with no variable represented more
than once.
A
sum term is the logical OR of one or
more literals,
with no variable represented more
than once.
The
following are all valid product terms over the two variables X and Y.
![]() ·
·![]()
![]() ·Y X·
·Y X·![]() X·Y
X·Y
Forms,
such as X·X·![]() and X·
and X·![]() ·Y are not considered, as X·X = X and
·Y are not considered, as X·X = X and
X·![]() = 0, so X·X·
= 0, so X·X·![]() = X·
= X·![]() and X·
and X·![]() ·Y = 0·Y = 0.
·Y = 0·Y = 0.
The
following are all valid sum terms over the two variables X and Y.
X + Y X + ![]()
![]() + Y
+ Y ![]() +
+ ![]()
Single
literals
According
to the strict definition, a single literal is either a sum term or a product
term,
depending on the context. This is
necessary to avoid having to give a number of special
cases in the following definitions.
Sum of
Products and Product of Sums
A
SOP (Sum of Products) expression is
the logical OR of product terms.
A
POS (Product of Sums) expression is
the logical AND of sum terms.
Sample SOP
expressions
F1(X,
Y) = X·Y + ![]() ·
·![]()
G1(X, Y) = ![]() ·Y + X·
·Y + X·![]()
H1(X, Y, Z) = X + ![]() ·Z
·Z
Note: If we did not allow single literals to be
product terms, we
would
have trouble classifying H(X, Y, Z), which is clearly SOP.
Sample POS
expressions
F2(X,
Y) = (X+Y) · (![]() +
+![]() )
)
G2(X, Y) = (![]() +Y) · (X+
+Y) · (X+![]() )
)
H2(X, Y, Z) = X·(![]() + Z)
+ Z)
Note: POS expressions almost always have
parentheses to indicate the
correct
evaluation.
More on
Ambiguous Forms
What
is the form of the expression F(X, Y) = X + Y
1. SOP It
is the logical OR of two product terms.
Each product term
is a single literal.
2. POS It
is a single sum term (X + Y)
Both
statements are true. In general,
questions such as this do not concern us.
If you are asked a question like this on a test, either answer will be
accepted.
This
ambiguity comes from the definitional necessity of mentioning “the logical AND
of one or more terms” and “the logical OR of one or more terms”.
With
two equally good answers to an ambiguous form, pick the one you like.
Inclusion
A
product term T1 is included in a product term T2
if every literal in T1
is also in T2.
A
sum term T1 is included in a sum term T2
if every literal in T1
is also in T2.
Consider
the following examples:
F(A,
B, C) = A·B + A·C + A·B·C
Each of A·B and A·C is included in A·B·C.
G(A,
B, C) = (A + B)·(A + C)·(A + B + C)
Each of (A + B) and (A +
C) is included in (A + B + C).
There
is no inclusion in the next expression
F(A,
B, C) = A·B + A·C + ![]() ·B·C
·B·C
The literal A does no
appear in the third term.
The
inclusion rule is based on literals, not just variables.
More on
Inclusion
Consider F1(A,
B, C) = A·B + A·C + A·B·C
and F2(A, B, C) = A·B + A·C
We
claim that the two are equal for every value of A, B, and C.
Let
A = 0
Clearly F1(A, B, C) = 0
F2(A, B,
C) = 0
Let
A = 1
Then F1(A, B, C) = B + C + B·C
and F2(A, B, C) = B + C
Notice
that we still have inclusion in F1, as each of B and C is included in B·C.
We prove these versions of F1(A, B, C) = F2(A, B, C) using a truth table.
|
B |
C |
B·C |
B + C |
B + C + B·C |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Last Word on
Inclusion
If
a SOP or POS expression has included terms, it can be simplified.
F1(A,
B, C) = A·B + A·C + A·B·C is identically equal to
F2(A, B, C) = A·B + A·C
G1(A,
B, C) = (A + B)·(A + C)·(A + B + C) is identically equal to
G2(A, B, C) = (A + B)·(A + C)
The
conclusion is that Boolean expressions with included terms are needlessly
complicated. We can simplify them by the
application of trivial rules.
Note
that duplication is a form of inclusion.
The
expression F3(A, B) = A·B + A·B has 2 terms, each included in the other.
Non–Standard
Expressions
Not
every useful Boolean expression is in a standard form.
F(X,
Y) = X Å Y is not a standard
form, due to the exclusive OR.
G(X,
Y) = X·Y + (X + Y)·(![]() +Y) is not in a standard form.
+Y) is not in a standard form.
This has both a product
term and a sum term.
The
fact that G(X, Y) can easily be converted to a standard form
does not make it already in a
standard form.
Let’s
convert this to SOP. I usually have
difficulty in conversion to POS,
unless I am using a method I have
yet to describe.
The
term X·Y is already a product
term, so we convert (X + Y)·(![]() +Y) to SOP.
+Y) to SOP.
(X + Y)·(![]() +Y) = X·(
+Y) = X·(![]() +Y) + Y·(
+Y) + Y·(![]() +Y)
+Y)
= X·![]() + X·Y + Y·
+ X·Y + Y·![]() + Y·Y
+ Y·Y
= 0 + X·Y+ ![]() ·Y + Y = (X +
·Y + Y = (X + ![]() )·Y + Y
)·Y + Y
= 1·Y + Y = Y
So G(X, Y) = X·Y + Y = Y G(X, Y) = Y.
More on
Non–Standard Forms
Look at the Boolean function G(X, Y) = X·Y + Y. There are two ways to at look at
this. Try both ways.
Let G(X, Y) = X·Y + Y = X·Y + 1·Y = (X + 1) ·Y = 1 ·Y = Y
Do a truth table proof of the equality.
|
X |
Y |
X·Y |
X·Y + Y |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Note that the column marked X·Y matches the one marked X·Y + Y. The two
functions are identical. Also note that the term Y is included in the term X·Y,
so that, by inclusión, the term X·Y can be eliminated from the expression.
Normal and
Canonical Forms
A
Normal SOP expression is a Sum of
Products expression
with no included product terms.
A
Normal POS expression is a Product
of Sums expression
with no included sum terms.
A
Canonical SOP expression over a set
of Boolean variables is
a Normal SOP expression in which
each product term contains
a literal for each of the Boolean
variables.
A
Canonical POS expression over a set
of Boolean variables is
a Normal POS expression in which
each sum term contains
a literal for each of the Boolean
variables.
Note: A canonical expression on N
Boolean variables is made up
of terms, each of which
has exactly N literals.
Note: One can do digital design based on either
normal or canonical forms.
The choice usually depends
on the technology used.
Equivalence
of Canonical Forms and Truth Tables
We
can directly translate between either of the canonical forms and
a truth table using a standard set of rules.
To
produce the Sum of Products
representation from a truth table,
a) Generate
a product term for each row where the value of the function is 1.
b) The
variable is complemented if its value in the row is 0, otherwise it is not.
To
produce the Product of Sums
representation from a truth table,
a) Generate
a sum term for each row where the value of the function is 0.
b) The
variable is complemented if its value in the row is 1, otherwise it is not.
|
Row |
X |
Y |
X Å Y |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
0 |
SOP: Terms for rows 1 and 2. Row 1: ![]() ·Y, Row 2: X·
·Y, Row 2: X·![]() F =
F = ![]() ·Y + X·
·Y + X·![]()
POS: Terms for rows 0 and 3. Row 0: (X + Y), Row 3: (![]() +
+ ![]() )
)
F = (X + Y)·(![]() +
+ ![]() )
)
SOP Example:
Truth Table to Canonical Form
To
produce the Sum of Products
representation from a truth table,
a) Generate
a product term for each row where the value of the function is 1.
b) The
variable is complemented if its value in the row is 0, otherwise it is not.
Here
again is the truth table.
|
Row |
A |
B |
C |
F2 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
The term is ![]() ·B·C
·B·C
The term is A·![]() ·C
·C
The term is A·B·![]()
The term is A·B·C
F2(A, B, C) = ![]() ·B·C + A·
·B·C + A·![]() ·C + A·B·
·C + A·B·![]() + A·B·C
+ A·B·C
Example:
Interpretation of a Digital Circuit
Here
is a sample problem, taken from the textbook The Essentials of Computer
Organization and Architecture by Linda Null and Julia Lobur.
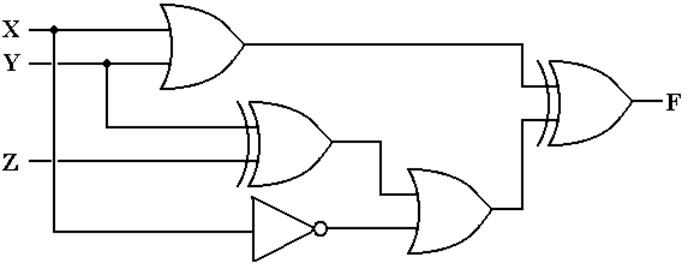
The
task is to represent this circuit by both a Boolean expression and a
Truth Table. Admittedly, this will prove
to be a silly circuit.
Interpreting
a Digital Circuit: Step 1
Label
the circuit elements (I have chosen to use numbers) and label the output
of each element. Note that we are slowly
building a Boolean expression.

The
outputs of each gate are as follows:
The output of gate 1 is (X + Y),
The output of gate 2 is (Y Å Z),
The output of gate 3 is X’,
The output of gate 4 is X’ + (Y Å Z), and
The output of gate 5 is (X + Y) Å [X’ + (Y Å Z)]
Interpreting
a Digital Circuit: Step 2
For
a circuit of this complexity, the best next step is to make a Truth Table.
|
X |
Y |
Z |
X + Y |
(Y Å Z) |
X’ |
X’ + (Y Å Z) |
(X + Y) Å [X’+(Y Å Z)] |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
We have now solved the
problem. I want to continue and produce
a simpler expression.
(At least I think that it is simpler).
Interpreting
a Digital Circuit: Step 3
Present
the truth table without the intermediate expressions. Use the standard rules
to convert the truth table to Canonical
SOP.
|
X |
Y |
Z |
F(X, Y, Z) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
F(X, Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X·Y’·Z’ + X·Y·Z
0 0
0 0 0 1 1
0 0
1 1 1
F(X,
Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X’·Y’·Z’ + X·Y’·Z’ + X·Y·Z
= X’·Y’·(Z’ + Z) + (X + X’)·Y’·Z’ + X·Y·Z
= X’·Y’ + Y’·Z’ + X·Y·Z
Building a
Digital Circuit for a Boolean Expression
We
take as examples two representations of the same Boolean expression.
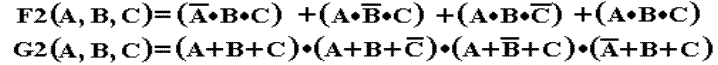
Sum of Products
SOP One OR gate connecting the output of a number
of AND gates.
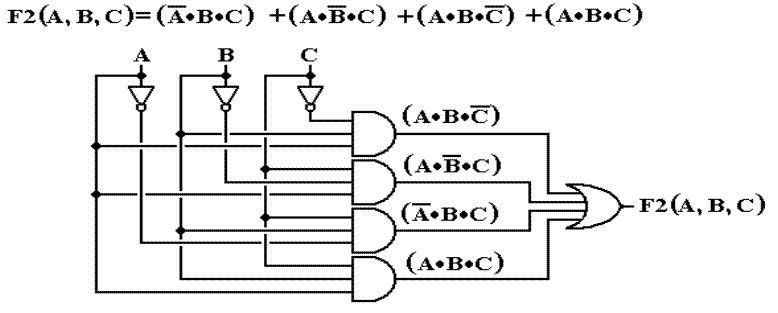
Building a
Digital Circuit (Part 2)
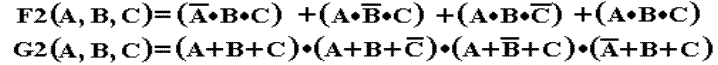
Product of Sums
POS One AND gate connecting the output of a number
of OR gates.
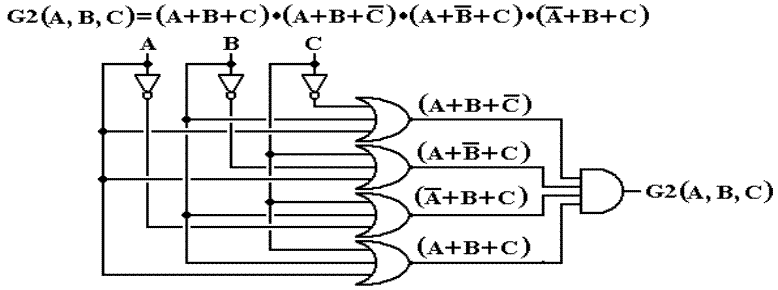
There
are simpler Boolean expressions that are equivalent to both F2 and G2,
which are equivalent to each other. We
study simplification later.
The
Tri–State Buffer
Some
time ago, we considered relays as automatic switches.
The tri–state buffer is also an automatic switch.
Here
are the diagrams for two of the four most popular tri–state buffers.

An enabled–low buffer is the
same as an enabled–high buffer with a NOT gate.
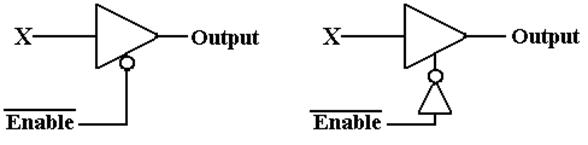
What
does a tri–state buffer do when it is enabled?
What does a tri–state buffer do when it is not enabled?
What is this third state implied by the name “tri–state”?
An
Enabled–High Tri–State Buffer
Consider
an enabled–high tri–state buffer, with the enable signal called “C”.
When C = 1, the buffer is enabled.
When C = 0, the buffer is not
enabled.
What
does the buffer do?
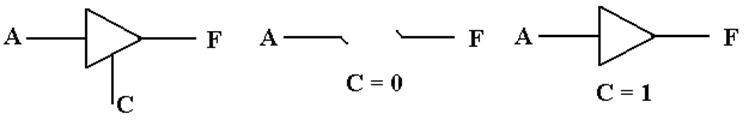
The
buffer should be considered a switch.
When C = 0, there is no connection between
the input A and the output F. When C =
1, the output F is connected to the input A via
what appears to be a non–inverting buffer.
Strictly
speaking, when C = 0 the output F remains connected to input A, but through a
circuit that offers very high resistance to the flow of electricity. For this reason, the
state is often called “high impedance”,
“impedance” being an engineer’s word for
“resistance”.
Sample Use
of Tri–State Buffers
Here
is a circuit that uses a pair of tri–state buffers to connect exactly
one of two inputs to an output. The
effect of the circuit is at right.
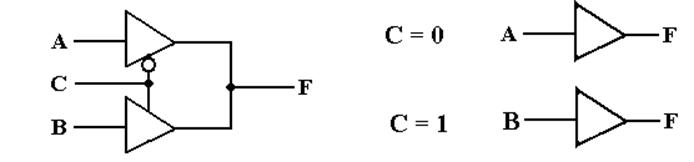
Here
is the equivalent circuit using the standard gates.
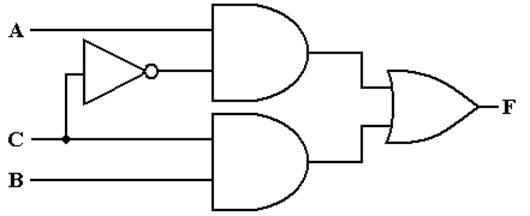
What is This
Third State?

The
following circuits show the effect of two tri–states. Here we see two
switches, either of which can illuminate
the light.

The
analogy is not exact, but the point is valid: neither switch is attempting
to assert zero volts.
Tristate
Buffers: Defining Voltages
Consider
the following diagram in the situation when the control
is low; C = 0.

What
is the voltage at the output of tristate buffer I?
The
voltage is not determined by that buffer, and is independent of A.
As
this point has a direct connection to the output of tristate buffer II, which
is active, the voltage at that point is determined by that tristate.
When
many tristate buffers output to a common circuit line, at most one of
them should be active at any time. Two
or more active is an error.