The Computer Memory

Chapter 6 forms the first of a two–chapter sequence on computer memory.

Topics for this chapter include.

1. A functional description of primary computer memory, sometimes
called by the obsolescent term “core memory”.

2. A description of the memory bus, including asynchronous and the
more modern synchronous busses.

3. Memory registers and memory timings.

4. Registers and flip–flops.

5. The basic memory unit.

6. The physical view of memory. How commercial memory is organized.

7. Managing the address: column address, row address, and strobes.

8. The evolution of modern memory chips.

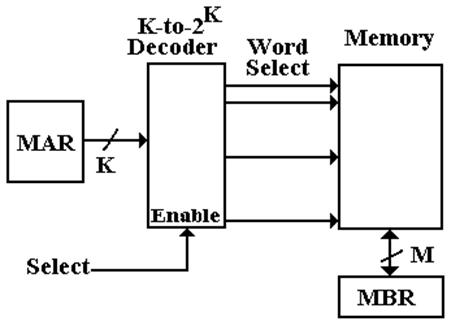
The Memory Component

The memory stores the instructions and data for an executing program.

Memory is characterized by the smallest addressable unit:
Byte addressable the smallest unit is an 8–bit byte.
Word addressable the smallest unit is a word, usually 16 or 32 bits in length.

Most modern computers are byte addressable, facilitating access to character data.

Logically, computer memory should be considered as an array.
The index into this array is called the address or “memory address”.

A logical view of such a byte addressable memory might be written in code as:

Const MemSize =
byte Memory[MemSize] // Indexed 0 … (MemSize – 1)

The CPU has two registers dedicated to handling memory.

The MAR (Memory Address Register) holds the address being accessed.

The MBR (Memory Buffer Register) holds the data being written to the
memory or being read from the memory. This is sometimes
called the Memory Data Register.

Requirements for a Memory Device

1. Random access by address, similar to use of an array. Byte addressable
memory can be considered as an array of bytes.
byte memory [N] // Address ranges from 0 to (N – 1)

2. Binary memory devices require two reliable stable states.

3. The transitions between the two stable states must occur quickly.

4. The transitions between the two stable states must not occur
spontaneously, but only in response to the proper control signals.

5. Each memory device must be physically small, so that a large number
may be placed on a single memory chip.

6. Each memory device must be relatively inexpensive to fabricate.

Varieties of Random Access Memory

There are two types of RAM

1. RAM read/write memory

2. ROM read–only memory.

The double use of the term “RAM” is just accepted. Would you say “RWM”?

Types of ROM

1. “Plain ROM” the contents of the memory are set at manufacture
and cannot be changed without destroying the chip.

2. PROM the contents of the chip are set by a special device
called a “PROM Programmer”. Once programmed
the contents are fixed.

3. EPROM same as a PROM, but that the contents can be erased
and reprogrammed by the PROM Programmer.

Memory Control Signals

Read / Write Memory must do three actions:

READ copy contents of an addressed word into the MBR

WRITE copy contents of the MBR into an addressed word

NOTHING the memory is expected to retain the contents written into
it until those contents have been rewritten.

One set of control signals Select# – the memory unit is selected.
R/W# if 0 the CPU writes to memory, if 1 the CPU reads from memory.

Select#	R/W#	Action
0	0	CPU writes data to the memory.
0	1	CPU reads data from the memory.
1	0	Memory contents are not changed.
1	1	Memory contents are not changed.

A ROM has only one control signal: Select.

If Select = 1 for a ROM, the CPU reads data from the addressed memory slot.

Memory Timings

Memory Access Time

Defined in terms of reading from memory. It is the time between the address
becoming stable in the MAR and the data becoming available in the MBR.

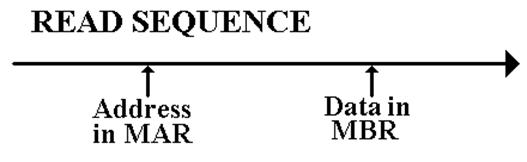
Memory Cycle Time

Less used, this is defined as the minimum time between two independent
memory accesses.

The Memory Bus

The memory bus is a dedicated point–to–point bus between the CPU and
computer memory. The bus has the following lines.

1. Address lines used to select the memory chip containing the addressed
memory word and to address that word within the memory.

These are used to generate the signal Select#, sent to each memory chip.

2. Data lines used to transfer data between the CPU and memory.

3. Bus Clock is present on a synchronous bus to coordinate transfers.

4. Control lines such as the R/W# control signal mentioned above.

Some control lines, called strobe lines, assert the validity of data on
associated lines.

When RAS (Row Address Strobe) is asserted, the row address on the
memory address line is certified to be a valid address.

A Synchronous Bus Timing Diagram

This is a bus read. The sequence: the address becomes valid, RD# is asserted,
and later the data become valid.
An Asynchronous Bus Timing Diagram

Here, the importance is the interplay of the Master Synchronization (MSYN#)
and Slave Synchronization (SSYN#) signals.

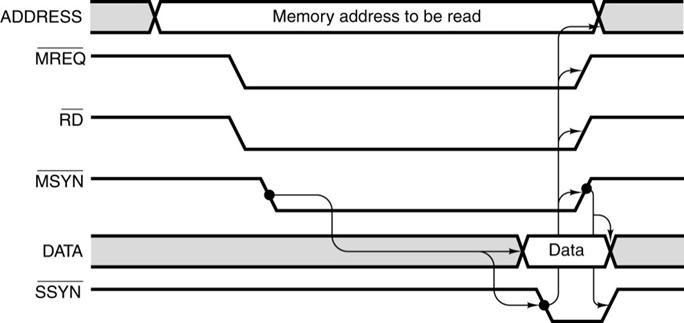
The sequence: 1. The address becomes valid; MREQ# and RD# are asserted low.
2. MSYN# is asserted low, causing the memory to react.
3. Data become valid and SSYN# is asserted low.
4. When SSYN# goes high, the data are no longer valid.

Sequential Circuits

Sequential circuits are those with memory, also called “feedback”. In this, they differ
from combinational circuits, which have no memory.

The stable output of a combinational circuit does not depend on the order in which its
inputs are changed. The stable output of a sequential circuit usually does depend
on the order in which the inputs are changed.

Sequential circuits can be used as memory elements; binary values can be stored in them.
The binary value stored in a circuit element is often called that element’s state.

All sequential circuits depend on a phenomenon called gate delay. This reflects the fact
that the output of any logic gate (implementing a Boolean function) does not change
immediately when the input changes, but only some time later.

The gate delay for modern circuits is typically a few nanoseconds.

Synchronous Sequential Circuits

We usually focus on clocked sequential circuits,
also called synchronous sequential circuits.

As the name “synchronous” implies, these circuits respond to a system clock,
which is used to synchronize the state changes of the various sequential circuits.

One textbook claims that “synchronous sequential circuits use clocks to order events.”
A better claim might be that the clock is used to coordinate events. Events that should
happen at the same time do; events that should happen later do happen later.

The system clock is a circuit that emits a sequence of regular pulses with a fixed and
reliable pulse rate. If you have an electronic watch (who doesn’t?), what you have is
a small electronic circuit emitting pulses and a counter circuit to count them.

Clock frequencies are measured in
kilohertz thousands of ticks per second
megahertz millions of ticks per second
gigahertz billions of ticks per second.

One can design asynchronous sequential circuits, which are not controlled by a system clock.
They present significant design challenges related to timing issues.

Views of the System Clock

There are a number of ways to view the system clock. In general, the view depends on the
detail that we need in discussing the problem. The logical view is shown in the next figure,
which illustrates some of the terms commonly used for a clock.

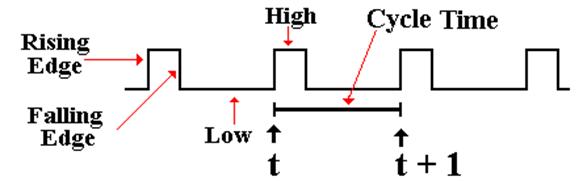
The clock is typical of a periodic function. There is a period t for which

f(t) = f(t + t)

This clock is asymmetric. It is often the case that the clock is symmetric, where the
time spent at the high level is the same as that at the low level. Your instructor often
draws the clock as asymmetric, just to show that such a design is allowed.

NOTATION: We always call the present clock tick “t” and the next one “t + 1”,
even if it occurs only two nanoseconds later.

Views of the System Clock

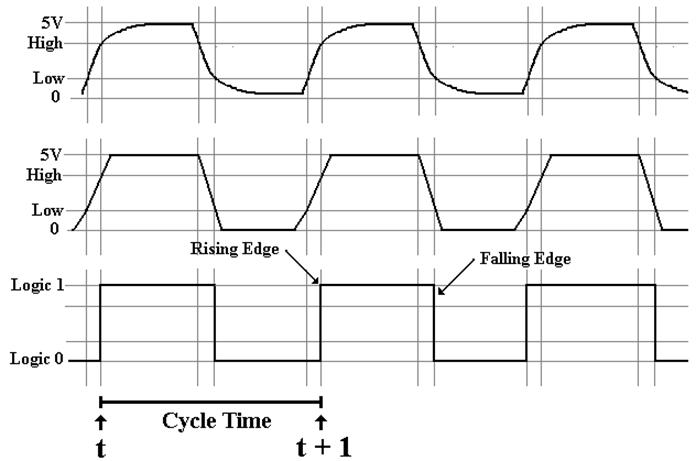
The top view is the “real physical view”. It is seldom used.
The middle view reflects the fact that voltage levels do not change instantaneously.
We use this view when considering system busses.

Clock Period and Frequency

If the clock period is denoted by t, then the frequency (by definition) is f = 1 / t.

For example, if t = 2.0 nanoseconds, also written as t = 2.0·10^–9 seconds, then
f = 1 / (2.0·10^–9 seconds) = 0.50·10⁹ seconds^–1 or 500 megahertz.

If f = 2.5 Gigahertz, also written as 2.5·10⁹ seconds^–1, then
t = 1.0 / (2.5·10⁹ seconds^–1) = 0.4·10^–9 seconds = 0.4 nanosecond.

Memory bus clock frequencies are in the range 125 to 1333 MHz (1.33 GHz).

CPU clock frequencies generally are in the 2.0 to 6.0 GHz range, with
2.0 to 3.5 GHz being far the most common.

The IBM z196 Enterprise Server contains 96 processors, each running at
5.2 GHz. Each processor is water cooled.

Latches and Flip–Flops: First Definition

We consider a latch or a flip–flop as a device that stores a single binary value.

Flip–flops and clocked latches are devices that accept input at fixed times dictated
by the system clock. For this reason they are called “synchronous sequential circuits”.

Denote the present time by the symbol t. Denote the clock period by t.

Rather than directly discussing the clock period, we merely say that
the current time is t
after the next clock tick the time is (t + 1)

The present state of the device is often called Q(t)
The next state of the device is often called Q(t + 1)

The sequence: the present state is Q(t), the clock “ticks”, the state is now Q(t + 1)

AGAIN: We call the next state Q(t + 1), even if the transition from Q(t) to
Q(t + 1) takes only a few nanoseconds. We are counting the actual
number of clock ticks, not the amount of time they take.

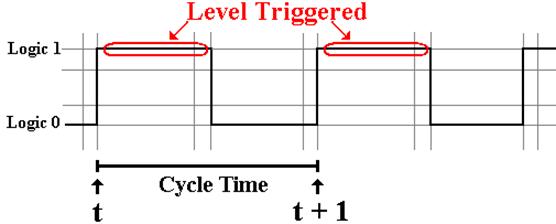
Latches and Flip–Flops: When Triggered

Clocked latches accept input when the system clock is at logic high.

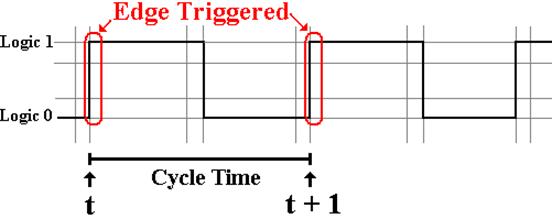
Flip–flops accept input on either the rising edge of the system clock.

Describing Flip–Flops

A flip–flop is a “bit bucket”; it holds a single binary bit.

A flip–flop is characterized by its current state: Q(t).

We want a way to describe the operation of the flip–flops.

How do these devices respond to the input? We use tables to describe the operation.

Characteristic tables: Given Q(t), the present state of the flip–flop, and
the input, what will Q(t + 1), the next state of the flip–flop, be?

Excitation tables: Given Q(t), the present state of the flip–flop, and
Q(t + 1), the desired next state of the flip–flop,
what input is required to achieve that change.

SR Flip–Flop

We now adopt a functional view. How does the next state depend on the present state
and input. A flip–flop is a “bit holder”.

Here is the diagram for the SR flip–flop.

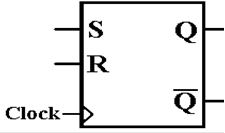
Here again is the state table for the SR flip–flop.

S	R	Q(t + 1)
0	0	Q(T)
0	1	0
1	0	1
1	1	ERROR

Note that setting both S = 1 and R = 1 causes the flip–flop to enter a logically
inconsistent state, followed by an undeterministic, almost random, state. For this
reason, we label the output for S = 1 and R = 1 as an error.

JK Flip–Flop

A JK flip–flop generalizes the SR to allow for both inputs to be 1.

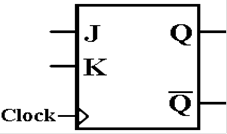
Here is the characteristic table for a JK flip–flop.

J	K	Q(t + 1)
0	0	Q(t)
0	1	0
1	0	1
1	1

Note that the flip–flop can generate all four possible functions of a single variable:
the two constants 0 and 1
the variables Q and .

The D Flip–Flop

The D flip–flop specializes either the SR or JK to store a single bit. It is very useful for
interfacing the CPU to external devices, where the CPU sends a brief pulse to set the
value in the device and it remains set until the next CPU signal.

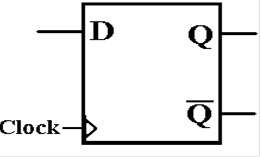
The characteristic table for the D flip–flop is so simple that it is expressed better as
the equation Q(t + 1) = D. Here is the table.

D	Q(t + 1)
0	0
1	1

The D flip–flop plays a large part in computer memory.

Some memory types are just large collections of D flip–flops.

The other types are not fabricated from flip–flops, but act as if they were.

The T Flip–Flop

The “toggle” flip–flop allows one to change the value stored. It is often used in circuits
in which the value of the bit changes between 0 and 1, as in a modulo–4 counter in which
the low–order bit goes 0, 1, 0, 1, 0, 1, etc.

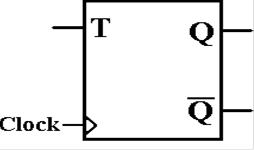
The characteristic table for the D flip–flop is so simple that it is expressed better as
the equation Q(t + 1) = Q(t) Å T. Here is the table.

T	Q(t + 1)
0	Q(t)
1

Memory Mapped Input / Output

Though not a memory issue, we now address the idea of memory mapped input
and output. In this scheme, we take part of the address space that would
otherwise be allocated to memory and allocate it to I/O devices.

The PDP–11 is a good example of a memory mapped device. It was a byte
addressable device, meaning that each byte had a unique address.

The old PDP–11/20 supported a 16–bit address space. This supported addresses
in the range 0 through 65,535 or 0 through 0177777 in octal.

Addresses 0 though 61,439 were reserved for physical memory.
In octal these addresses are given by 0 through 167,777.

Addresses 61,440 through 65,535 (octal 170,000 through 177,777) were
reserved for registers associated with Input/Output devices.

Examples: CR11 Card Reader 177,160 Control & Status Register
177,162 Data buffer 1
177,164 Data buffer 2

Reading from address 0177162 would access the card reader data buffer.

The Linear View of Memory

Memory may be viewed as a linear array, for example a byte–addressable memory

byte memory [N] ; // Addresses 0 .. (N – 1)

This is a perfectly good logical view, it just does not correspond to reality.

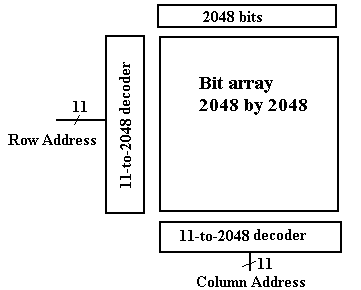
Memory Chip Organization

Consider a 4 Megabit memory chip, in which each bit is directly addressable.
Recall that 4M = 2²² = 2¹¹ · 2¹¹, and that 2¹¹ = 2, 048.

The linear view of memory, on the previous slide, calls for a 22–to–2²² decoder,
also called a 22–to–4,194,304 decoder. This is not feasible.

If we organize the memory as a two–dimensional grid of bits, then the design
calls for two 11–to–2048 decoders. This is still a stretch.

Managing Pin-Outs

Consider now the two–dimensional memory mentioned above. What pins are needed?

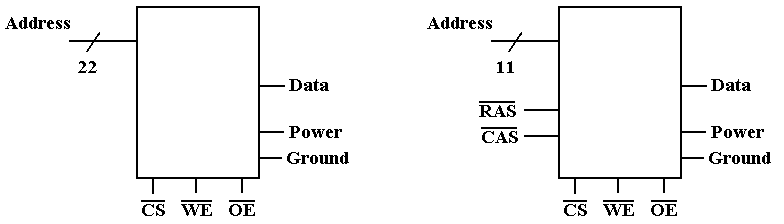
Pin Count
Address Lines 22 Address Lines 11
Row/Column 0 Row/Column 2
Power & Ground 2 Power & Ground 2
Data 1 Data 1
Control 3 Control 3
Total 28 Total 19

Separate row and column addresses require two cycles to specify the address.

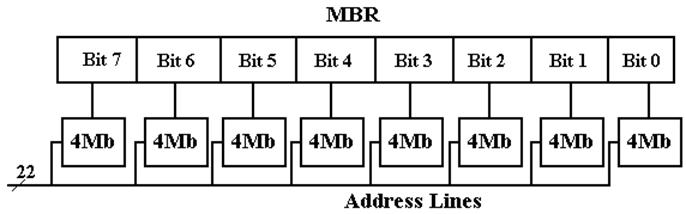
Four–Megabyte Memory

Do we have a single four–megabyte chip or eight four–megabit memory chips?

One common solution is to have bit–oriented chips. This facilitates the
two–dimensional addressing discussed above.

For applications in which data integrity is especially important, one might add a
ninth chip to hold the parity bit. This reflects the experience that faults, when
they occur, will be localized in one chip.

Parity provides a mechanism to detect, but not correct, single bit errors.

Correction of single bit errors requires twelve memory chips. This scheme will
also detect all two–bit errors.

Memory Interleaving

Suppose a 64MB memory made up of the 4Mb chips discussed above.
We now ignore parity memory, for convenience and also because it is rarely needed.

We organize the memory into 4MB banks, each having eight of the 4Mb chips.
The figure in the slide above shows such a bank.

The memory thus has 16 banks, each of 4MB.

16 = 2⁴ 4 bits to select the bank
4M = 2²² 22 bits address to each chip

Not surprisingly, 64M = 2²⁶.

Low–Order Interleaving

Bits	25 – 4	3 – 0
Use	Address to the chip	Bank Select

High–Order Interleaving (Memory Banking)

Bits	25 – 22	21 – 0
Use	Bank Select	Address to the chip

Most designs use low order interleaving to reduce effective memory access times.

Faster Memory Chips

We can use the “2 dimensional” array approach, discussed earlier, to create a faster
memory. This is done by adding a SRAM (Static RAM) buffer onto the chip. Consider
the 4Mb (four megabit) chip discussed earlier, now with a 2Kb SRAM buffer.

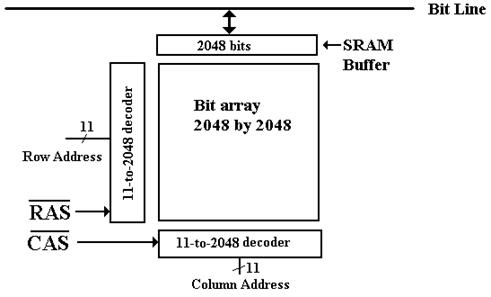
In a modern scenario for reading the chip, a Row Address is passed to the chip, followed
by a number of column addresses. When the row address is received, the entire row is
copied into the SRAM buffer. Subsequent column reads come from that buffer.

Memory Technologies: SRAM and DRAM

One major classification of computer memory is into two technologies

SRAM Static Random Access Memory

DRAM Dynamic Random Access Memory (and its variants)

SRAM is called static because it will keep its contents as long as it is powered.

DRAM is called dynamic because it tends to lose its contents, even when powered.
Special “refresh circuitry” must be provided.

Compared to DRAM, SRAM is
faster
more expensive
physically larger (fewer memory bits per square millimeter)

SDRAM is a Synchronous DRAM.
It is DRAM that is designed to work with a Synchronous Bus, one with a clock signal.

The memory bus clock is driven by the CPU system clock, but it is always slower.

SDRAM (Synchronous DRAM)

Synchronous Dynamic Random Access Memory

Suppose a 2 GHz system clock. It can easily generate the following memory bus clock
rates: 1GHz, 500 MHz, 250MHz, 125MHz, etc. Other rates are also possible.

Consider a 2 GHz CPU with 100 MHz SDRAM.
The CPU clock speed is 2 GHz = 2,000 MHz
The memory bus speed is 100 MHz.

In SDRAM, the memory transfers take place on a timing dictated by the memory
bus clock rate. This memory bus clock is always based on the system clock.

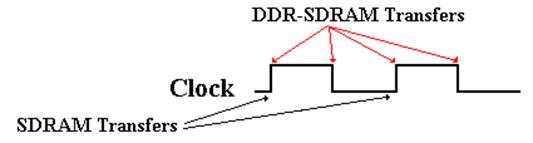
In “plain” SDRAM, the transfers all take place on the rising edge of the memory
bus clock. In DDR SDRAM (Double Data Rate Synchronous DRAM), the transfers
take place on both the rising and falling clock edges.

Speed Up Access by Interleaving Memory

We have done all we can to make the memory chips faster.
How do we make the memory itself faster with the chips we have?

Suppose an 8–way low–order interleaved memory. The chip timings are:

Cycle time: 80 nanoseconds between independent memory reads

Access time 40 nanoseconds to place requested data in the MBR.

Each chip by itself has the following timing diagram.

This memory chip can be accessed once every 80 nanoseconds.

The Same Memory with 8–Way Interleaving

Suppose a set of sequential read operations, beginning at address 1000.
The interleaving is low–order.

Chip 0 has addresses 1000, 1008, 1016, etc.

Chip 1 has addresses 1001, 1009, 1017, etc.

Chip 7 has addresses 1007, 1015, 1023, etc.

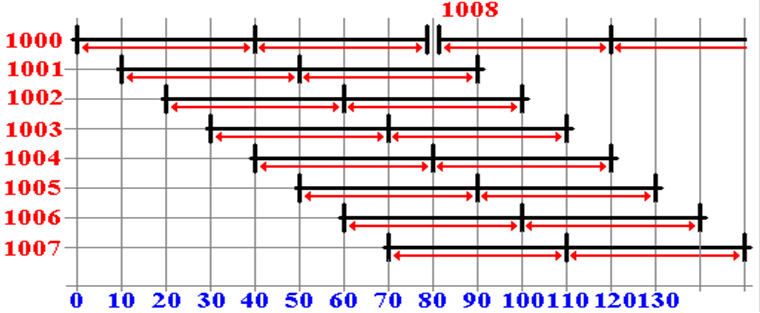
Note that the accesses can be overlapped, with a net speedup of 8X.

Latency and Bandwidth

Look again at this figure.

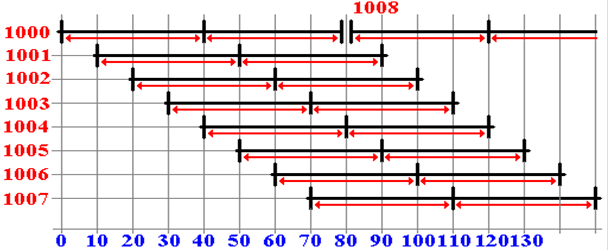
Each memory bank has a cycle time of 80 nanoseconds.

The first memory request takes 40 nanoseconds to complete.

The first time is called latency. This is the time interval between the first
request and its completion.

After that, there is one result every 10 nanoseconds. As a bandwidth, this
is 100 million transfers per second.

Fat Data Busses

Here is another trick to speed up memory transfers.

In the above example, we assumed that the memory was byte addressable,
having an 8–bit data bus between it and the CPU.

At one transfer every 10 nanoseconds, this is 100 megabytes per second.

Our simplistic analysis assumed that these transfers were directly to the CPU.

When we discuss cache memory, we shall see that the transfers are between
main memory and the L2 (Level 2) cache memory – about 1 MB in size.

Suppose that the main feature of the L2 cache is an 8–byte cache line.

For now, this implies that 8 byte transfers between the L2 cache and main
memory are not only easy, but also the most natural unit of transaction.

We link the L2 cache and main memory with 64 data lines, allowing 8 bytes
to be moved for each memory transfer. We now have 800 megabytes/sec.

More on SDRAM

“Plain” SDRAM makes a transfer every cycle of the memory bus.
For a 100 MHz memory bus, we would have 100 million transfers per second.

DDR–SDRAM is Double Data Rate SDRAM

DDR–SDRAM makes two transfers for every cycle of the memory bus,
one on the rising edge of the clock cycle
one on the falling edge of the clock cycle.

For a 100 MHz memory bus, DDR–SDRAM would have 200 million transfers per second.

To this, we add wide memory buses. A typical value is a 64–bit width.

A 64–bit wide memory bus transfers 64 bits at a time. That is 8 bytes at a time.

Thus our sample DDR–SDRAM bus would transfer 1,600 million bytes per second.

This might be called 1.6 GB / second, although it more properly is 1.49 GB / second,
as 1 GB = 1, 073, 741, 824 bytes.

Evolution of Modern Memory

Here are some actual cost & performance data for memory.

Year	Cost per MB in US $	Actual component		Speed nsec.	Type
		Size (KB)	Cost
1957	411,041,792.00	0.0098	392.00	10,000	transistors
1959	67,947,725.00	0.0098	64.80	10,000	vacuum tubes
1965	2,642,412.00	0.0098	2.52	2,000	core
1970	734,003.00	0.0098	0.70	770	core
1975	49,920.00	4	159.00	??	static RAM
1981	4,479.00	64	279.95	??	dynamic RAM
1985	300.00	2,048	599.00	??	DRAM
1990	46.00	1,024	45.50	80	SIMM
1996	5.25	8,192	42.00	70	72 pin SIMM
2001	15¢	128 MB	18.89	133 MHz	DIMM
2006	7.3¢	2,048 MB	148.99	667 MHz	DIMM DDR2
2008	1.0¢	4,096 MB	39.99	800 MHz	DIMM DDR2
2010	1.22¢	8,192 MB	99.99	1333 MHz	DIMM DDR2