The Return
Address
It is the idea
of a return address that distinguishes a subprogram call
from another type of branch instruction.
A subprogram
call involves an unconditional transfer of control to code at another
address, called the EA or Effective Address.
After execution
of the subprogram, control returns to the next instruction.
The situation
just before the call is shown below. At this
point, the IP
(Instruction Pointer) had already been moved to the next instruction.

The execution of
the CALL involves three tasks:
1. Computing
the value of the Effective Address (EA).
2. Storing
the current value of the Instruction Pointer (IP)
so that it can be
retrieved when the subroutine returns.
3. Setting
the IP = EA, the address of the first instruction in the subroutine.
Issues with the
Subprogram Call
There
are a number of issues to be addressed when designing a mechanism
for subprogram invocation.
1. How
to store the return address and retrieve it when needed.
2. How
to communicate parameter values to the called subprogram.
3. How
to return function values. This question
holds also for Java methods.
We
discuss these issues in reverse order.
Function values are almost
always returned in a general purpose register that is
standard for the programming language and its run–time system.
For
programs run on the IA–32, this is likely the 32–bit register EAX.
In
the CDC–6600 and CDC–7600 series, a single precision result was returned in the
standard register X6, and a double precision in the pair (X6, X7).
For
Java, the value is returned at the top of the operand stack, ready to be
popped.
In
Java, the return value may be an object reference, so that an object can be
returned.
Communicating
Parameter Values
The
idea of a subprogram is based on the passing and returning of parameter values.
There
are many methods for passing parameter values.
The
two common methods are call by reference
and call by value.
In
the call by value protocol, it is
the value of the argument that is passed.
Any
changes made to that argument are local to the subprogram and not returned.
Consider
the following code fragments.
Main Sub1
X =
2 SUB1 (ByValue X)
CALL SUB1(X) X = X + 1
Y = X PRINT X
PRINT Y RETURN
When
the subprogram prints the value, it prints a 3.
When the main program prints the value, it prints a 2.
Note
that the change in the value of X is not communicated back to the calling
program.
Call By
Reference
In
the call by reference protocol, it
is the address of the variable that is passed.
Value
changes made in the subprogram are communicated back to the caller.
Consider
the following code fragments.
Main Sub1
X =
2 SUB1 (ByReference X)
CALL SUB1(X) X = X + 1
Y = X PRINT X
PRINT Y RETURN
When
the subprogram prints the value, it prints a 3.
When the main program prints the value, it also prints a 3.
The
C and C++ languages do things a bit differently.
All
parameters are passed by value.
Call
by reference is done by passing the value of the address of the variable.
Call By Reference (C/C++ Style)
Consider the
following line of C++ code, adapted from the book by Rob Williams.
n = average (10,
math_scores)
This might be implemented in assembly language as
follows:
LEA EAX, math_scores // Get address of the array
PUSH EAX // Push the address
PUSH 0Ah // Push hexadecimal A,
// which is
decimal 10
CALL average
We
shall discuss the use of the stack for parameter passing soon.
The
C/C++ convention calls for right–to–left pushing onto the stack.
Storing the
Return Address
The
key advantage of the subprogram structure is that a return address can be
stored. This enables program execution
to resume at the instruction immediately
following the call instruction.
Question: How is this return address to be
stored?
There
are a number of ways to store the return address so that it can be accessed
on the return to the calling program.
Efficiency
The
efficient methods store the return address in a fixed location.
The
IBM System/360 specification calls for the return address to be stored in
a designated general purpose register.
The
CDC–6600 and similar computers call for the return address to be stored in
the body of the called subprogram.
Each
of these is very efficient, but neither will support recursion.
Flexibility
The
more flexible, and modern, approach is to use a stack to store the return
address.
The Original Way
to Store the Return Address
The
simplest way is to store the return address in the subroutine.
This
is the method used by many older computers, such as the CDC–6600.
A
subprogram at address Z would be invoked by a call such as JSR Z.
The return address would be stored at address Z and execution begin at (Z + 1).
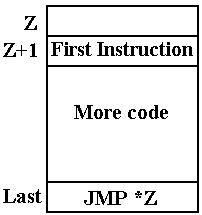
Note
that the last executable instruction is an indirect jump.
1. Go
to address Z and get the contents of that address.
2. Use
the contents of that address as the target address for the jump.
The Original IBM
System/360 Convention
The
convention calls for using one of the general–purpose registers to store the
return address. In this example, I use
register 8, which is a common choice.
Calling the
subroutine
BAL (Branch and
Link) is one of the two instructions used for subroutine invocation.
Here
is a sample of the code BAL
8,P10PAGE
NEXT
Another Instruction
This
instance of the instruction stores the return address in register 8 and then
executes an unconditional branch to the subroutine P10PAGE.
Here,
the return address is associated with the label NEXT; for the next instruction.
Returning from
the subroutine
This
instruction is used to return from execution of the subroutine. It is an unconditional
jump to an address contained in the register.
Obviously,
the subroutine cannot change the value stored in this register.
An
example of such an instruction is BR 8
Sample CDC–6600
Call (Not Recursive)
Suppose
the following instructions
100 JSR
200
101 Next
Instruction
200 Holder
for Return Address
201 First
Instruction
Last BR
*200
After
the subroutine call, we would have
100 JSR
200
101 Next
Instruction
200 101
201 First
Instruction
Last BR
*200
The
BR*200 would cause a branch to address 101, thus causing a proper return.
Sample CDC–6600
Call (Try At Recursion)
Suppose
a five instruction subroutine at address 200.
Address
200 holds the return address and addresses 201 – 205 hold the code.
This
subroutine contains a single recursive call to itself that will be executed
once.
Called from First Recursive First
address 100 Call Return
200 101 200 204 200 204
201 Inst
1 201 Inst 1 201 Inst 1
202 Inst
2 202 Inst 2 202 Inst 2
203 JSR
200 203 JSR 200 203 JSR 200
204 Inst
4 204 Inst 4 204 Inst
4
205 BR
* 200 205 BR * 200 205 BR * 200
Note
that the original return address has been overwritten.
As
long as the subroutine is returning to itself, there is no difficulty.
It
will never return to the original calling routine.
Writing
Recursive Subroutines
We
note immediately that neither of the above methods will support recursion,
because each will lose track of return addresses.
The
standard way to track return addresses is to use a stack.
Here is how the use of a stack corrects the problem above.
Main
calls the subroutine SP ® 101
The
subroutine calls itself SP ® 204 ® 101
First
return Pop the return address from
the stack
RA = 204
SP ® 101
The
subroutine returns to itself.
Second return Pop the return address from the stack
RA = 101
The
subroutine returns to the main program.
Tail Recursion
A
subprogram is called “tail recursive”
if the recursive call is the
last executable statement in the subprogram.
Modern
compilers can convert tail recursive subprograms into non–recursive
equivalents that use iteration. These
are far more efficient.
The
best example is the factorial function.
Integer Factorial (Integer N)
If (N < 2) Then Return 1 ;
Else Return N*Factorial(N
– 1);
Here
is the equivalent code that would be actually compiled to machine language.
Integer Factorial (Integer N)
Integer F = 1 ;
For (Integer K = N, K > 1, K--)
Do F = F * K ;
Return F ;
Stack Protocols
This
example shows a standard protocol that is implemented on top of hardware.
The
hardware supports the protocol, but does not dictate it.
It
is the standard RTS (Run Time System) associated
with a give high–level language
that contains the implementation details, such as
1. How
to manage the system stack.
2. How
to pass the return address to a subprogram.
3. How
to pass arguments to the subprogram and return function values.
4. How
to allocate memory for variables local to the subprogram.
Most
standard designs use the following convention.
JSR will
push the return address to the stack.
RET will
pop the return address from the stack.
Most
modern protocols provide for use of the stack to hold values other than the
return address. We shall develop this
idea when we discuss the stack frame.
Management
of Dynamic Memory
In
order to understand the use of a stack in managing subprograms, we must
first see the stack as one of two important dynamic data structures.
The
stack is a LIFO (Last In – First Out) data structure that is quite useful in
allocation
of memory for subprogram calls: return address, local variables, arguments,
etc.
The
heap is a semi–structured data
collection used to allocate memory for dynamic
variables that are created by operators such as the Java new()
or C++ malloc().
Typically,
a RTS (Run Time System) will allocate a block of memory to be shared
between the stack and the heap, without setting direct limits on either.
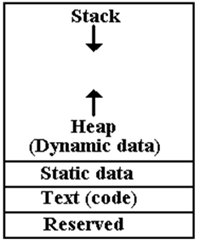 The standard
arrangement is to have the stack start at high
The standard
arrangement is to have the stack start at high
addresses and grow towards low addresses.
The
heap starts at low addresses and grows toward the high.
In
the MIPS memory allocation
the stack pointer is initialized to 0x7FFF FFFC, and
the heap pointer is initialized to 0x1000 8004.
The
two grow towards each other.
The
IA–32 Stack
The
tendency of the stack to grow down gives rise to a situation that
is not intuitive. The stack top is the
lowest address on the stack.
The
IA–32 architecture calls for stacking only 32–bit values.
The
following diagram might reflect the memory map associated with
the stack on an IA–32 machine.
In
this example the values were pushed in this order: 6 (first), 5, 4, 3, and then
2.

The
stack top has the lowest address.
Implementation
of the Stack Operations
As noted above, the stack grows toward more negative
addresses.
Given this we have two options for implementing PUSH,
each giving rise to a unique implementation of POP.
Option PUSH X POP
Y
1 M[SP] = X SP = SP + 1 // Post–decrement on PUSH
SP
= SP – 1 Y =
M[SP]
2 SP = SP – 1 Y = M[SP] // Pre–decrement on PUSH
M[SP]
= X SP = SP +
1
As
far as I can determine, the Java standard requires only that the stack
operations
be implemented as a consistent pair that preserve the idea of a stack top.
At
this point, either option is equally viable.
The
IA–32 Stack Protocol
More
properly, this is the MS–DOS and MS–Windows protocol.
This
protocol is uniform for the run time systems that support compilers for
high–level languages run under MS–DOS and MS–Windows.
This
protocol uses two registers found in the IA–32.
ESP The
32–bit stack pointer, used to indicate the top of the stack.
EBP The
32–bit base pointer, used to manipulate the stack frame.
More on this later.
The
stack protocol is pre–decrement, post–increment.
PUSH ESP = ESP -
4 // Decrement the stack pointer
MEM[ESP] = VALUE // Place the item on the stack
POP VALUE =
MEM[ESP] // Get the value
ESP = ESP + 4 // Increment the stack pointer
The
RTS calls for only 32–bit values to be stored on the stack.
Example:
The Stack for the Return Address
Here
are two fragments of code to illustrate the stack use for return addresses.
First, we have a fragment of the calling code.
N = 3
M = FACT(N)
A1: J = M*3 //
A silly statement, get the label
Here
is the function, written in an “expanded style” to facilitate discussion.
INTEGER FACT (INTEGER
L)
K1 = 1 ;
IF (L > 1) THEN
L2 = L – 1;
K2 = FACT(L2);
A2: K1 = L*K2 ;
END IF ;
RETURN K1 ; // Question: What is the return address?
// Does this return to
A1 or A2?
Follow
the Stack (Part 1)
M
= FACT(N)
 The return
address placed on the stack is that
The return
address placed on the stack is that
of a statement in the calling program.
L
= 3, L2 = 2. K2 = FACT(L2)
 Here, this is
called from within the FACT function.
Here, this is
called from within the FACT function.
It is the return address within the function that is
stored on the stack.
Follow
the Stack (Part 2)
L
= 2, L2 = 1. K2 = FACT(L2)
 The return
address within the function is again placed onto
The return
address within the function is again placed onto
the stack. The function is called with L
= 1.
The
function returns with value 1
K2 = FACT(L2);
A2: K1 = L*K2 ;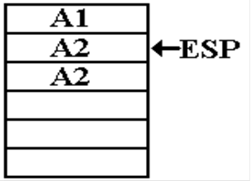
Here
L = 2. The function computes K1 = 2, and
returns to the address indicated at the top of the stack.
The
function returns again.
Follow
the Stack (Part 3)
The
function returns with value 2. The state
of the stack is now as follows.
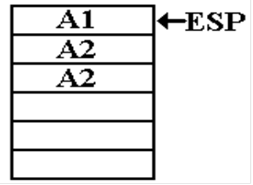
K2 = FACT(L2);
A2: K1 = L*K2 ;
Here
K2 = 2 and L = 3. K1 = 6.
The function returns to address A1 with a value of 6.
But
note that there is another problem. How
are the local variables stored?
First
call L = 3 L2 = 2 K2
= 2 K1 = 6
Second
call L = 2 L2 = 1 K2
= 1 K1 = 2
Third
call L = 1 L2 is not used. K2 not used K1 = 1
The
values K1 and K2 are computed after the return from the recursive call, so
they are not critical. The value L2 is
computed and used only in the call, so it
is not critical either. It is the value
of L that must be correct when needed.
Use the Stack for Arguments
We
have described the use of the stack to handle return addresses.
We
now extend this discussion to the use of the stack for passing arguments.
The
two common ways to pass an argument are call
by value (passing the value of the
argument) and call by reference
(passing the address of the argument).
At
this level, we just consider proper stack handling of 32–bit parameters, which
might
be values or addresses. The basic
mechanism is independent of the parameter’s use.
Here
is the basic script at this point.
1. Push
the parameters onto the stack.
For call by value, push
the value of the argument.
For call by reference,
push the address of the argument.
2. Push
the return address onto the stack.
3. The
called routine accesses the stack to get at the parameters.
4. The
called routine pops the return address from the stack and returns.
Two Calling Conventions
Consider
the high–level language statement.
PROCA (L, M, N)
In what order
are the arguments pushed onto the stack?
In the Pascal
convention, the arguments are pushed left–to–right.
The sequence for
a Pascal–like language would be
PUSH L
PUSH M
PUSH N
CALL PROCA
In the C/C++
convention, the arguments are pushed right–to–left.
The sequence for
a C–like language would be
PUSH N
PUSH M
PUSH L
CALL PROCA
The
CALL instruction pushes the return address onto the stack.
MS–Windows Uses the Pascal Calling Convention
Though
mostly written in C and C++, MS–Windows uses the Pascal convention.
Here is a sample header description for a MS–Windows API function.
BOOL WINAPI CopyFileEx(
__in LPCTSTR lpExistingFileName,
__in LPCTSTR lpNewFileName,
__in_opt LPPROGRESS_ROUTINE lpProgressRoutine,
__in_opt LPVOID lpData,
__in_opt
LPBOOL pbCancel,
__in DWORD dwCopyFlags
);
BOOL The function returns a Boolean value:
TRUE or FALSE.
WINAPI This is a descriptor for the calling
convention used. This is
the new name
for the older __stdcall name, which itself
replaces
the name __pascal, for the Pascal convention.
CALL PROCA (L, M, N)
Here
we assume the C/C++ style of pushing arguments, right to left.
This
slide overlooks several mistakes in order to make a single point.
The correct version of the stack will be given very soon.
Suppose
that this is the state of the stack on entry to the subprogram PROCAA.
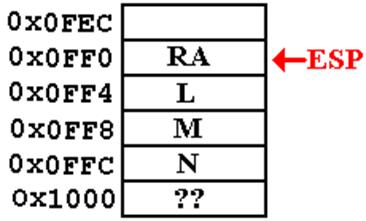 The dynamic idea
is to access arguments by offsets
The dynamic idea
is to access arguments by offsets
from values stored in registers, such as ESP.
At
this point, the addresses of the arguments are fixed with
respect to the ESP. Why not use these
offsets?
CAUTION: This
is not what a debugger will show if stopped before the first
executable
statement of the subroutine.
There is special
entry code, which we shall discuss very soon.
The Stack Frame
The stack frame, also known as the “call stack”, is the basic mechanism for
storing
variables that are local to a called subprogram.
In the
terminology of C and C++, these are called “automatic variables”.
These variables
have meaning only within the called subprogram itself.
Suppose that the
subprogram PROCA used four 32–bit
variables I, J, K
and K1.
The entry code
for PROCA would allocate 4 stack slots to hold
these variables.
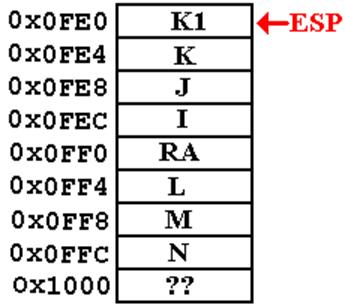 This entry code
is executed immediately upon
This entry code
is executed immediately upon
entry to the subprogram, before the first
executable line of the subprogram.
Again, this is
not quite the complete picture.
We shall evolve that soon.
Note for the
moment that this might complicate
the use of ESP as a base register for addressing
the arguments that were passed.
The Run–Time Stack – Not Quite the ADT
In
the traditional ADT (Abstract Data Type) stack, the only data movement
operators are PUSH and POP. The stack is
not manipulated by other operators.
The
RTS (Run Time System) will simply subtract a value
from the stack pointer
in order to allocate space on the stack for local variable storage..
Space
for four local 32–bit variables would be allocated by setting SP = SP – 0x10.
Before After
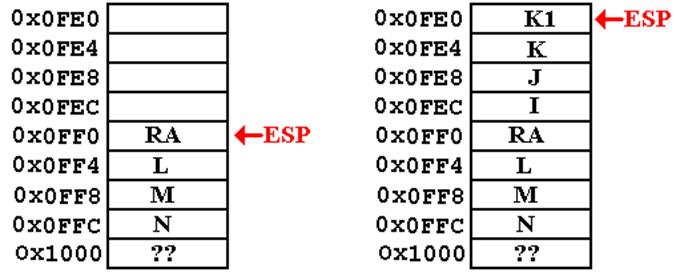
At
this point, I is at ESP + 12, J at ESP + 8, K at ESP + 4, and K1 at ESP.
The Base Pointer EBP
Again,
we note that the picture at this point is not quite complete.
We
need one more feature to complete the design of a stack frame.
We
now discuss the mechanism chosen to allow for register & offset access to
items
in the stack without directly using the stack pointer, ESP.
The
mechanism is called the frame pointer
or the base pointer.
In the IA–32, this is the function of the 32–bit EBP register.
The
base pointer will be used to reference:
1. The
parameters passed to the subprogram , and
2. The
variables local to the subprogram.
This
frees the design to allow the stack pointer, ESP, to vary in accordance with
the needs of stack management.
Creating the Stack Frame
When a
subprogram is invoked, the run–time system software creates a new
stack frame.
Here is the complete
procedure for creation of the stack frame, as implemented
in the IA–32 architecture.
1. The
passed arguments, if any, are pushed onto the stack.
2. The
CALL instruction causes the return address to be pushed onto the stack.
3. Before
the execution of the first code in the subprogram, EBP is pushed onto
the stack. This is the base pointer of the calling procedure.
This is pushed onto the stack, so that
it can be restored on return.
4. EBP
is set to the value stored in ESP;
thereafter in the routine it is used to access
the subroutine parameters as well
as any local variables.
5. Space
is allocated on the stack to store any variables local to the subprogram.
This is done by subtracting a
value from the ESP.
6. If
the subprogram is written to store and restore values in the registers, these
are pushed onto the stack before
being altered.
Example Call
Here
is a simple implementation of the function, written in Pseudo–Java.
INT PROCA
(INT I, INT J, INT K)
{
INT K1 ;
K1 = I + J
+ K ; // K1 is a 32-bit value.
RETURN K1 ;
}
Assuming
that the variables L, M, and N have been properly initialized,
this might be invoked as follows:
K2 = PROCA
(L, M, N) ;
A Possible Assembly Language Implementation of the Call
In
this, we assume that the register EAX is use to return the function value.
Here
is a possible assembly language implementation.
; K2 = PROCA (L, M, N)
0x3FFC PUSH
EAX // Save the value of EAX
0x4000 PUSH
N
0x4004 PUSH
M
0x4008 PUSH
L
0x400C CALL
PROCA
0x4010 ADD
ESP, 12 // Clear parameters from stack
0x4014 MOV K2,
EAX
0x4018 POP
EAX // Get the old EAX back.
Some
implementations might not save the value of the register used to
return the function value.
This
code choice just shows what is possible.
Step–By–Step Illustration of the Stack
In
this illustration, we assume that the arguments have the following values.
L
= 16 (0x10)
M
= 32 (0x20)
N
= 50 (0x32)
We
assume some addresses for the stack.
In particular, that ESP = 0x1000 before the call
is executed.
Assume
that, just before the call, the registers EAX and EBP
have the following values.
EAX
contains 0x2222
EBP
contains 0x100C.
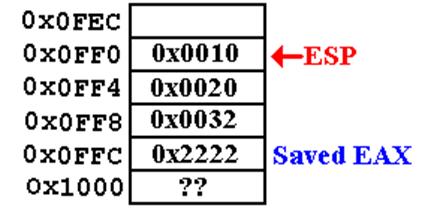
Call Sequence (Page 1)
Step
1: The value of EAX is first pushed onto
the stack.
The three argument values
are then pushed onto the stack.
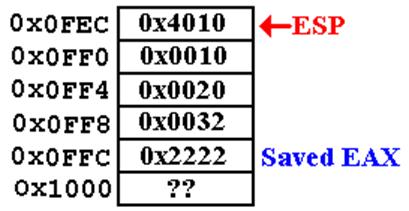
Step
2: The CALL instruction causes the
return address to be pushed onto the stack.
Call Sequence (Page 2)
At
this point, we need to base our discussion on the assembly language.
Begin
with the entry code, which precedes any declaration or executable HLL code.
; INT PROCA
(INT I, INT J, INT K)
PUSH
EBP ; Save the old value of EBP
MOV EBP,
ESP ; Set EBP for this stack frame.

Call Sequence (Page 3)
; INT K1 ;
SUB ESP,
4 ; Set aside room for K1
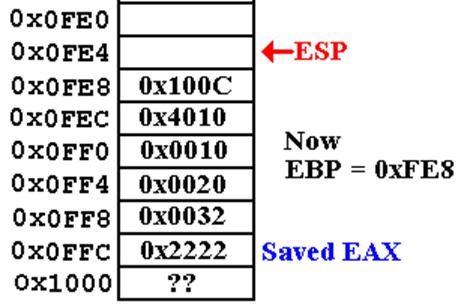
Notice
the amount of assembly language code executed before the first
executable line of the high level language.
One
must understand this in order to read the stack correctly.
Call Sequence (Page 4)
; K1 = I +
J + K ;
MOV EAX,
[EBP + 8] ; Get value
ADD EAX,
[EBP + 12]
ADD EAX,
[EBP + 16]
MOV [EBP
– 4], EAX

Call Sequence (Page 4)
The
first part of the return sequence sets the value of EAX to the return
value.
Then
the process of clearing the stack frame begins, by resetting ESP
almost
to the value needed for the return.
; RETURN K1
;
MOV EAX,
[EBP – 4]
MOV ESP,
EBP

Call Sequence (Page 5)
The
next part of the return sequence sets the value of EBP to its saved
value.
POP EBP
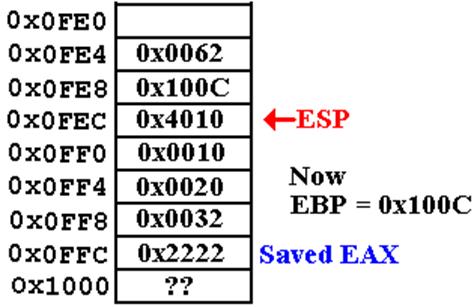
Call Sequence (Page 6)
The
final part of the return sequence pops the return address and executes the
return.
RET
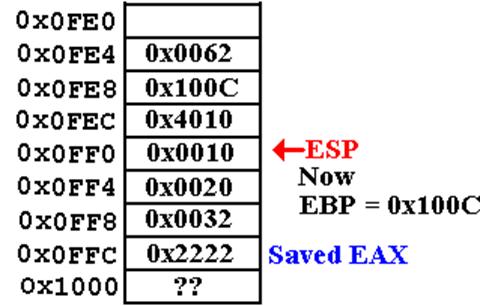
The Return Sequence in the Calling Code
0x4010 ADD
ESP, 12 // Clear parameters from stack
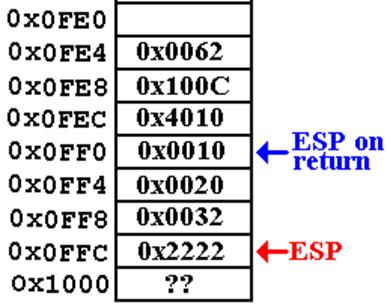
0x4014 MOV K2, EAX
0x4018 POP
EAX // Get the old EAX back.