The Memory Hiierarchy

SDRAM – Synchronous Dynamic Random Access Memory

As we mentioned above, the relative slowness of memory as compared to the CPU has long
been a point of concern among computer designers. One recent development that is used to
address this problem is SDRAM – synchronous dynamic access memory.

The standard memory types we have discussed up to this point are
      SRAM      Static Random Access Memory
                        Typical access time: 5 – 10 nanoseconds
                        Implemented with 6 transistors: costly and fairly large.

      DRAM     Dynamic Random Access Memory
                        Typical access time: 50 – 70 nanoseconds
                        Implemented with one capacitor and one transistor: small and cheap.

In a way, the desirable approach would be to make the entire memory to be SRAM. Such a
memory would be about as fast as possible, but would suffer from a number of setbacks,
including very large cost (given current economics a 256 MB memory might cost in excess of
$20,000) and unwieldy size. The current practice, which leads to feasible designs, is to use large
amounts of DRAM for memory. This leads to an obvious difficulty.

      1)      The access time on DRAM is almost never less than 50 nanoseconds.
      2)      The clock time on a moderately fast (2.5 GHz) CPU is 0.4 nanoseconds,
               125 times faster than the DRAM.

The problem that arises from this speed mismatch is often called the “Von Neumann Bottleneck”
– memory cannot supply the CPU at a sufficient data rate. Fortunately there have been a number
of developments that have alleviated this problem. We will soon discussed the idea of cache
memory, in which a large memory with a 50 to 100 nanosecond access time can be coupled with
a small memory with a 10 nanosecond access time. While cache memory does help, the main
problem is that main memory is too slow.

In his 2010 book [R033], William Stallings introduced his section on advanced DRAM
organization (Section 5.3, pages 173 to 179) with the following analysis of standard memory
technology, which I quote verbatim.

“As discussed in Chapter 2 [of the reference], one of the most critical system
bottlenecks when using high–performance processors is the interface to main
internal memory. This interface is the most important pathway in the entire
computer system. The basic building block of memory remains the DRAM
chip, as it has for decades; until recently, there had been no significant changes
in DRAM architecture since the early 1970s. The traditional DRAM chip is
constrained both by its internal architecture and by its interface to the
processor’s memory bus.”

Modern computer designs, in an effort to avoid the Von Neumann bottleneck, use several tricks,
including multi–level caches and DDR SDRAM main memory. We continue to postpone the
discussion of cache memory, and focus on methods to speed up the primary memory in order to
make it more compatible with the faster, and more expensive, cache.

Many of the modern developments in memory technology involve Synchronous Dynamic
Random Access Memory, SDRAM for short. Although we have not mentioned it, earlier
memory was asynchronous, in that the memory speed was not related to any external speed. In
SDRAM, the memory is synchronized to the system bus and can deliver data at the bus speed.
The earlier SDRAM chips could deliver one data item for every clock pulse; later designs called
DDR SDRAM (for Double Data Rate SDRAM) can deliver two data items per clock pulse.
Double Data Rate SDRAM (DDR–SDRAM) doubles the bandwidth available from SDRAM
by transferring data at both edges of the clock.

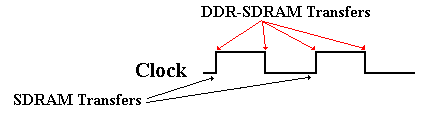
Figure: DDR-SDRAM Transfers Twice as Fast

As an example, we quote from the Dell Precision T7500 advertisement of June 30, 2011. The
machine supports dual processors, each with six cores. Each of the twelve cores has two 16 KB
L1 caches (an Instruction Cache and a Data Cache) and a 256 KB (?) L2 cache. The processor
pair shares a 12 MB Level 3 cache. The standard memory configuration calls for
4GB or DDR3 memory, though the system will support up to 192 GB. The memory bus
operates at 1333MHz (2666 million transfers per second). If it has 64 data lines to the L3 cache
(following the design of the Dell Dimension 4700 of 2004), this corresponds to
2.666·10⁹ transfers/second · 8 bytes/transfer » 2.13·10¹⁰ bytes per second. This is a peak
transfer rate of 19.9 GB/sec.

The SDRAM chip uses a number of tricks to deliver data at an acceptable rate. As an example,
let’s consider a modern SDRAM chip capable of supporting a DDR data bus. In order to
appreciate the SDRAM chip, we must begin with simpler chips and work up.

We begin with noting an approach that actually imposes a performance hit – address
multiplexing. Consider an NTE2164, a typical 64Kb chip. With 64K of addressable units, we
would expect 16 address lines, as 64K = 2¹⁶. In stead we find 8 address lines and two additional
control lines
Row Address Strobe (Active Low)
Column Address Strobe (Active Low)

Here is how it works. Recalling that 64K = 2¹⁶ = 2⁸ · 2⁸ = 256 · 256, we organize the memory
as a 256-by-256 square array. Every item in the memory is uniquely identified by two addresses
– its row address and its column address.

Here is the way that the 8-bit address is interpreted.

		Action
0	0	An error – this had better not happen.
0	1	It is a row address (say the high order 8-bits of the 16-bit address)
1	0	It is a column address (say the low order 8-bits of the 16-bit address)
1	1	It is ignored.

Here is that way that the NTE2164 would be addressed.
1) Assert = 0 and place the A₁₅ to A₈ on the 8–bit address bus.
2) Assert = 0 and place A₇ to A₀ on the 8–bit address bus.

There are two equivalent design goals for such a design.
      1)      To minimize the number of pins on the memory chip. We have two options:
                        8 address pins, RAS, and CAS (10 pins), or
                        16 address pins and an Address Valid pin (17 pins).

2) To minimize the number of address–related lines on the data bus.
The same numbers apply here: 10 vs. 17.

With this design in mind, we are able to consider the next step in memory speed-up. It is
called Fast-Page Mode DRAM, or FPM–DRAM.

Fast-Page Mode DRAM implements page mode, an improvement on conventional DRAM in
which the row-address is held constant and data from multiple columns is read from the sense
amplifiers. The data held in the sense amps form an “open page” that can be accessed relatively
quickly. This speeds up successive accesses to the same row of the DRAM core.

The move from FPM–DRAM to SDRAM is logically just making the DRAM interface
synchronous to the data bus in being controlled by a clock signal propagated on that bus. The
design issues are now how to create a memory chip that can respond sufficiently fast. The
underlying architecture of the SDRAM core is the same as in a conventional DRAM.
SDRAM transfers data at one edge of the clock, usually the leading edge.

So far, we have used a SRAM memory as a L1 cache to speed up effective memory access time
and used Fast Page Mode DRAM to allow quick access to an entire row from the DRAM chip.
We continue to be plagued with the problem of making the DRAM chip faster. If we are to use
the chip as a DDR–SDRAM, we must speed it up quite a bit.

Modern DRAM designs are increasing the amount of SRAM on the DRAM die. In most cases
a memory system will have at least 8KB of SRAM on each DRAM chip, thus leading to the
possibility of data transfers at SRAM speeds.

We are now faced with two measures: latency and bandwidth.
      Latency is the amount of time for the memory to provide the first element of a block
      of contiguous data.
      Bandwidth is the rate at which the memory can deliver data once the row address
      has been accepted.

One can increase the bandwidth of memory by making the data bus “wider” – that is able to
transfer more data bits at a time. It turns out that the optimal size is half that of a cache line in
the L2 cache. Now – what is a cache line?

In order to understand the concept of a cache line, we must return to our discussion of cache
memory. What happens when there is a cache miss on a memory read? The referenced byte
must be retrieved from main memory. Efficiency is improved by retrieving not only the byte
that is requested, but also a number of nearby bytes.

Cache memory is organized into cache lines. Suppose that we have a L2 cache with a cache line
size of 16 bytes. Data could be transferred from main memory into the L2 cache in units of 8 or
16 bytes. This depends on the size of the memory bus; 64 or 128 bits.

Suppose that the byte with address 0x124A is requested and found not to be in the L2 cache. A
cache line in the L2 cache would be filled with the 16 bytes with addresses ranging from 0x1240
through 0x124F. This might be done in two transfers of 8 bytes each.

We close this part of the discussion by examining some specifications of a memory chip that as
of July 2011 seemed to be state-of-the-art. This is the Micron DDR2 SDRAM in 3 models
               MT46H512M4         64 MEG x 4 x 8 banks
               MT47H256M8         32 MEG x 8 x 8 banks
               MT47H128M16       16 MEG x 16 x 8 banks

Collectively, the memories are described by Micron [R89] as “high-speed dynamic random–
access memory that uses a 4ns–prefetch architecture with an interface designed to transfer two
data words per clock cycle at the I/O bond pads.” But what is “prefetch architecture”?

According to Wikipedia [R034]

“The prefetch buffer takes advantage of the specific characteristics of memory
accesses to a DRAM. Typical DRAM memory operations involve three phases
(line precharge, row access, column access). Row access is … the long and slow
phase of memory operation. However once a row is read, subsequent column
accesses to that same row can be very quick, as the sense amplifiers also act as
latches. For reference, a row of a 1Gb DDR3 device is 2,048 bits wide, so that
internally 2,048 bits are read into 2,048 separate sense amplifiers during the row
access phase. Row accesses might take 50 ns depending on the speed of the
DRAM, whereas column accesses off an open row are less than 10 ns.”

“In a prefetch buffer architecture, when a memory access occurs to a row the buffer
grabs a set of adjacent datawords on the row and reads them out ("bursts" them) in
rapid-fire sequence on the IO pins, without the need for individual column address
requests. This assumes the CPU wants adjacent datawords in memory which in
practice is very often the case. For instance when a 64 bit CPU accesses a 16 bit
wide DRAM chip, it will need 4 adjacent 16 bit datawords to make up the full 64
bits. A 4n prefetch buffer would accomplish this exactly ("n" refers to the IO width
of the memory chip; it is multiplied by the burst depth "4" to give the size in bits of
the full burst sequence).”

“The prefetch buffer depth can also be thought of as the ratio between the core
memory frequency and the IO frequency. In an 8n prefetch architecture (such as
DDR3), the IOs will operate 8 times faster than the memory core (each memory
access results in a burst of 8 datawords on the IOs). Thus a 200 MHz memory core
is combined with IOs that each operate eight times faster (1600 megabits/second).
If the memory has 16 IOs, the total read bandwidth would be 200 MHz x 8
datawords/access x 16 IOs = 25.6 gigabits/second (Gbps), or 3.2 gigabytes/second
(GBps). Modules with multiple DRAM chips can provide correspondingly higher
bandwidth.”

Each is compatible with 1066 MHz synchronous operation at double data rate. For the
MT47H128M16 (16 MEG x 16 x 8 banks, or 128 MEG x 16), the memory bus can apparently be
operated at 64 times the speed of internal memory; hence the 1066 MHz.

Here is a functional block diagram of the 128 Meg x 16 configuration, taken from the Micron
reference [R91]. Note that there is a lot going on inside that chip.

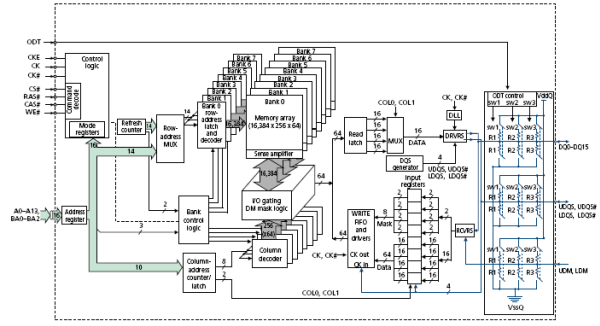
Here are the important data and address lines to the memory chip.

A[13:0] The address inputs; either row address or column address.

DQ[15:0] Bidirectional data input/output lines for the memory chip.

A few of these control signals are worth mention. Note that most of the control signals are
active–low; this is denoted in the modern notation by the sharp sign.

      CS#       Chip Select. This is active low, hence the “#” at the end of the signal name.
                    When low, this enables the memory chip command decoder.
                    When high, is disables the command decoder, and the chip is idle.

RAS# Row Address Strobe. When enabled, the address refers to the row number.

CAS# Column Address Strobe. When enabled, the address refers to the column

WE# Write Enable. When enabled, the CPU is writing to the memory.

The following truth table explains the operation of the chip.

CS#	RAS#	CAS#	WE#	Command / Action
1	d	d	d	Deselect / Continue previous operation
0	1	1	1	NOP / Continue previous operation
0	0	1	1	Select and activate row
0	1	0	1	Select column and start READ burst
0	1	0	0	Select column and start WRITE burst

The Cache Model

The next figure shows a simple memory hierarchy, sufficient to illustrate the two big ideas
about multi–level memory: cache memory and virtual memory.

Figure: The Memory Hierarchy with Cache and Virtual Memory

We consider a multi-level memory system as having a faster primary memory and a slower
secondary memory. In cache memory, the cache is the faster primary memory and the main
memory is the secondary memory. We shall ignore virtual memory at this point.

Program Locality: Why Does A Cache Work?

The design goal for cache memory is to create a memory unit with the performance of SRAM,
but the cost and packaging density of DRAM. In the cache memory strategy, a fast (but small)
SRAM memory fronts for a larger and slower DRAM memory. The reason that this can cause
faster program execution is due to the principle of locality, first discovered by Peter J. Denning
as part of his research for his Ph.D. The usual citation for Denning’s work on program locality is
his ACM paper [R78].

The basic idea behind program locality is the observed behavior of memory references; they tend
to cluster together within a small range that could easily fit into a small cache memory. There
are generally considered to be two types of locality. Spatial locality refers to the tendency of
program execution to reference memory locations that are clustered; if this address is accessed,
then one very near it will be accessed soon. Temporal locality refers to the tendency of a
processor to access memory locations that have been accessed recently. In the less common case
that a memory reference is to a “distant address”, the cache memory must be loaded from another
level of memory. This event, called a “memory miss”, is rare enough that most memory
references will be to addresses represented in the cache. References to addresses in the cache are
called “memory hits”; the percentage of memory references found in the cache is called the
“hit ratio”.

It is possible, though artificial, to write programs that will not display locality and thus defeat the
cache design. Most modern compilers will arrange data structures to take advantage of locality,
thus putting the cache system to best use.

Effective Access Time for Multilevel Memory

We have stated that the success of a multilevel memory system is due to the principle of locality.
The measure of the effectiveness of this system is the hit ratio, reflected in the effective access
time of the memory system.

We shall consider a multilevel memory system with primary and secondary memory. What we
derive now is true for both cache memory and virtual memory systems. In this course, we shall
use cache memory as an example. This could easily be applied to virtual memory.

In a standard memory system, an addressable item is referenced by its address. In a two level
memory system, the primary memory is first checked for the address. If the addressed item is
present in the primary memory, we have a hit, otherwise we have a miss. The hit ratio is defined
as the number of hits divided by the total number of memory accesses; 0.0 £ h £ 1.0. Given a
faster primary memory with an access time T_P and a slower secondary memory with access time
T_S, we compute the effective access time as a function of the hit ratio. The applicable formula is
T_E = h·T_P + (1.0 – h)·T_S.

RULE: In this formula we must have T_P < T_S. This inequality defines the terms “primary”
and “secondary”. In this course T_P always refers to the cache memory.

For our first example, we consider cache memory, with a fast cache acting as a front-end for
primary memory. In this scenario, we speak of cache hits and cache misses. The hit ratio is
also called the cache hit ratio in these circumstances. For example, consider T_P = 10
nanoseconds and T_S = 80 nanoseconds. The formula for effective access time becomes
T_E = h·10 + (1.0 – h)·80. For sample values of hit ratio

Hit Ratio Access Time

0.5 45.0

0.9 17.0

0.99 10.7

The reason that cache memory works is that the principle of locality enables high values of the
hit ratio; in fact h ³ 0.90 is a reasonable value. For this reason, a multi-level memory structure
behaves almost as if it were a very large memory with the access time of the smaller and faster
memory. Having come up with a technique for speeding up our large monolithic memory, we
now investigate techniques that allow us to fabricate such a large main memory.

Cache Memory Organization

We now turn our attention to strategies for organizing data in a cache. While this discussion is
cast in terms of a single–level cache, the basic principles apply to every level in a
multi–level cache. In this section, we use the term “memory”, sometimes “secondary
memory”, to refer to the memory attached to the cache. It is possible that this memory is either
the primary DRAM or a slower and larger cache

The mapping of the secondary memory to the smaller cache is “many to one” in that each cache
block can contain a number of secondary memory addresses. To compensate for each of these,
we associate a tag with each cache block, also called a “cache line”.

For example, consider a byte–addressable memory with 24–bit addresses and 16 byte blocks.
The memory address would have six hexadecimal digits. Consider the 24–bit address
0xAB7129. The block containing that address contains every item with address beginning with
0xAB712: 0xAB7120, 0xAB7121, … , 0xAB7129, 0xAB712A, … 0xAB712F.

We should point out immediately that the secondary memory will be divided into blocks of size
identical to the cache line. If the secondary memory has 16–byte blocks, this is due to the
organization of the cache as having cache lines holding 16 bytes of data.

The primary block would have 16 entries, indexed 0 through F. It would have the 20–bit tag
0XAB712 associated with the block, either explicitly or implicitly.

At system start–up, the faster cache contains no valid data, which are copied as needed from
the slower secondary memory. Each block would have three fields associated with it

The tag field identifying the memory addresses contained

Valid bit set to 0 at system start–up.
set to 1 when valid data have been copied into the block

            Dirty bit          set to 0 at system start–up.
                                    set to 1 whenever the CPU writes to the faster memory
                                    set to 0 whenever the contents are copied to the slower memory.

The basic unit of a cache is called a “cache line”, which comprises the data copied from the
slower secondary memory and the required ID fields. A 16–KB cache might contain 1,024
cache lines with the following structure.

D bit	V Bit	Tag	16 indexed entries (16 bytes total)
0	1	0xAB712	M[0xAB7120] … M[0xAB712F]

We now face a problem that is unique to cache memories. How do we find an addressed item?
In the primary memory, the answer is simple; just go to the address and access the item. The
cache has much fewer addressable entities than the secondary memory. For example, this cache
has 16 kilobytes set aside to store a selection of data from a 16 MB memory. It is not possible to
assign a unique address for each possible memory item.

The choice of where in the cache to put a memory block is called the placement problem. The
method of finding a block in the cache might be called the location problem. We begin with the
simplest placement strategy. When a memory block is copied into a cache line, just place it in
the first available cache line. In that case, the memory block can be in any given cache line. We
now have to find it when the CPU references a location in that block.

The Associative Cache

The most efficient search strategy is based on associative memory, also called content
addressable memory. Unlike sequential searches or binary search on an array, the contents of
an associative memory are all searched at the same time. In terminology from the class on
algorithm analysis, it takes one step to search an associative memory.

Consider an array of 256 entries, indexed from 0 to 255 (or 0x0 to 0xFF). Suppose that we are
searching the memory for entry 0xAB712. Normal memory would be searched using a
standard search algorithm, as learned in beginning programming classes. If the memory is
unordered, it would take on average 128 searches to find an item. If the memory is ordered,
binary search would find it in 8 searches.

Associative memory would find the item in one search. Think of the control circuitry as
“broadcasting” the data value (here 0xAB712) to all memory cells at the same time. If one of
the memory cells has the value, it raises a Boolean flag and the item is found.

We do not consider duplicate entries in the associative memory. This can be handled by some
rather straightforward circuitry, but is not done in associative caches. We now focus on the use
of associative memory in a cache design, called an “associative cache”.

Assume a number of cache lines, each holding 16 bytes. Assume a 24–bit address. The simplest
arrangement is an associative cache. It is also the hardest to implement.

Divide the 24–bit address into two parts: a 20–bit tag and a 4–bit offset. The 4–bit offset is
used to select the position of the data item in the cache line.

Bits	23 – 4	3 – 0
Fields	Tag	Offset

A cache line in this arrangement would have the following format.

D bit	V Bit	Tag	16 indexed entries
0	1	0xAB712	M[0xAB7120] … M[0xAB712F]

The placement of the 16 byte block of memory into the cache would be determined by a cache
line replacement policy. The policy would probably be as follows:
1. First, look for a cache line with V = 0. If one is found, then it is “empty”
and available, as nothing is lost by writing into it.

2. If all cache lines have V = 1, look for one with D = 0. Such a cache line
can be overwritten without first copying its contents back to main memory.

When the CPU issues an address for memory access, the cache logic determines the part that is
to be used for the cache line tag (here 0xAB712) and performs an associative search on the tag
part of the cache memory. Only the tag memory in an associative cache is set up as true
associative memory; the rest is standard SRAM. One might consider the associative cache as
two parallel memories, if that helps.

After one clock cycle, the tag is either found or not found. If found, the byte is retrieved. If not,
the byte and all of its block are fetched from the secondary memory.

The Direct Mapped Cache

This strategy is simplest to implement, as the cache line index is determined by the address.
Assume 256 cache lines, each holding 16 bytes. Assume a 24–bit address. Recall that 256 = 2⁸,
so that we need eight bits to select the cache line.

Divide the 24–bit address into three fields: a 12–bit explicit tag, an 8–bit line number, and a
4–bit offset within the cache line. Note that the 20–bit memory tag is divided between the
12–bit cache tag and 8–bit line number.

Bits	23 – 12	11 – 4	3 – 0
Cache View	Tag	Line	Offset
Address View	Block Number		Offset

Consider the address 0xAB7129. It would have
                                 Tag =                              0xAB7
                                Line =                              0x12
                            Offset =                              0x9

Again, the cache line would contain M[0xAB7120] through M[0xAB712F]. The cache line
would also have a V bit and a D bit (Valid and Dirty bits). This simple implementation often
works, but it is a bit rigid. Each memory block has one, and only one, cache line into which it
might be placed. A design that is a blend of the associative cache and the direct mapped cache
might be useful.

An N–way set–associative cache uses direct mapping, but allows a set of N memory blocks to
be stored in the line. This allows some of the flexibility of a fully associative cache, without the
complexity of a large associative memory for searching the cache.

Suppose a 2–way set–associative implementation of the same cache memory. Again assume 256
cache lines, each holding 16 bytes. Assume a 24–bit address. Recall that 256 = 2⁸, so that we
need eight bits to select the cache line. Consider addresses 0xCD4128 and 0xAB7129. Each
would be stored in cache line 0x12. Set 0 of this cache line would have one block, and set 1
would have the other.

Entry 0

Entry 1

Tag

Contents

Tag

Contents

0xCD4

M[0xCD4120] to

M[0xCD412F]

0xAB7

M[0xAB7120] to M[0xAB712F]

Examples of Cache Memory

We need to review cache memory and work some specific examples. The idea is simple, but
fairly abstract. We must make it clear and obvious. To review, we consider the main memory of
a computer. This memory might have a size of 384 MB, 512 MB, 1GB, etc. It is divided into
blocks of size 2^K bytes, with K > 2.

In general, the N–bit address is broken into two parts, a block tag and an offset.
The most significant (N – K) bits of the address are the block tag
The least significant K bits represent the offset within the block.

We use a specific example for clarity.
We have a byte addressable memory, with a 24–bit address.
The cache block size is 16 bytes, so the offset part of the address is K = 4 bits.

In our example, the address layout for main memory is as follows:
Divide the 24–bit address into two parts: a 20–bit tag and a 4–bit offset.

Bits	23 – 4	3 – 0
Fields	Tag	Offset

Let’s examine the sample address, 0xAB7129, in terms of the bit divisions above.

Bits:	23 – 20	19 – 16	15 – 12	11 – 8	7 – 4	3 – 0
Hex Digit	A	B	7	1	2	9
Field	0xAB712					0x09

So, the tag field for this block contains the value 0xAB712. The tag field of the cache line must
also contain this value, either explicitly or implicitly. It is the cache line size that determines the
size of the blocks in main memory. They must be the same size, here 16 bytes.

All cache memories are divided into a number of cache lines. This number is also a power of
two. Our example has 256 cache lines. Where in the cache is the memory block placed?

Associative Cache

As a memory block can go into any available cache line, the cache tag must represent
the memory tag explicitly: Cache Tag = Block Tag. In our example, it is 0xAB712.

Direct Mapped and Set–Associative Cache

For any specific memory block, there is exactly one cache line that can contain it.

Suppose an N–bit address space. 2^L cache lines, each of 2^K bytes.

Address Bits	(N – L – K) bits	L bits	K bits
Cache Address	Cache Tag	Cache Line	Offset
Memory Address	Memory Block Tag		Offset

To retrieve the memory block tag from the cache tag, just append the cache line number.

In our example: The Memory Block Tag         = 0xAB712
                         Cache Tag                              = 0xAB7
                        Cache Line                              = 0x12

Reading From and Writing to the Cache

Let’s begin our review of cache memory by considering the two processes: CPU Reads from
Cache and CPU Writes to Cache.

Suppose for the moment that we have a direct mapped cache, with line 0x12 as follows:

Tag	Valid	Dirty	Contents (Array of 16 entries)
0xAB7	1	0	M[0xAB7120] to M[0xAB712F]

Since the cache line has contents, by definition we must have Valid = 1. For this example,
we assume that Dirty = 0 (but that is almost irrelevant here).

Read from Cache.

The CPU loads a register from address 0xAB7123. This is read directly from the cache.

Write to Cache

The CPU copies a register into address 0xAB712C. The appropriate page is present in the cache
line, so the value is written and the dirty bit is set; Dirty = 1. Note that the dirty bit is not tested,
it is just set to 1. All that matters is that there has been at least one write access to this cache
line.

Here is a question that cannot occur for reading from the cache. Writing to the cache has
changed the value in the cache. The cache line now differs from the corresponding block in
main memory. Eventually, the value written to the cache line must be copied back to the
secondary memory, or the new value will be lost. The two main solutions to this problem are
called “write back” and “write through”.

Write Through

In this strategy, every byte that is written to a cache line is immediately written back to the
corresponding memory block. Allowing for the delay in updating main memory, the cache line
and cache block are always identical. The advantage is that this is a very simple strategy. No
“dirty bit” needed. The disadvantage in the simple implementation is that writes to cache
proceed at main memory speed. Many modern primary memories now have a write queue,
which is a fast memory containing entries to be written to the slower memory. As long as the
queue does not fill, it can accept data at cache speeds.

Write Back

In this strategy, CPU writes to the cache line do not automatically cause updates of the
corresponding block in main memory.

The cache line is written back only when it is replaced. The advantage of this is that it is a faster
strategy. Writes always proceed at cache speed. Furthermore, this plays on the locality theme.
Suppose each entry in the cache is written, a total of 16 cache writes. At the end of this
sequence, the cache line will eventually be written to the slower memory. This is one slow
memory write for 16 cache writes. The disadvantage of this strategy is that it is more complex,
requiring the use of a dirty bit.

Cache Line Replacement

Assume that memory block 0xAB712 is present in cache line 0x12. We now get a memory
reference to address 0x895123. This is found in memory block 0x89512, which must be placed
in cache line 0x12. The following holds for both a memory read from or memory write to
0x895123. The process is as follows.

1. The valid bit for cache line 0x12 is examined. If (Valid = 0), there is nothing
in the cache line, so go to Step 5.

2. The memory tag for cache line 0x12 is examined and compared to the desired
tag 0x895. If (Cache Tag = 0x895) go to Step 6.

3. The cache tag does not hold the required value. Check the dirty bit.
If (Dirty = 0) go to Step 5.

4. Here, we have (Dirty = 1). Write the cache line back to memory block 0xAB712.

5. Read memory block 0x89512 into cache line 0x12. Set Valid = 1 and Dirty = 0.

6. With the desired block in the cache line, perform the memory operation.

We have three different major strategies for cache mapping.

Direct Mapping is the simplest strategy, but it is rather rigid. One can devise “almost realistic”
programs that defeat this mapping. It is possible to have considerable page replacement with a
cache that is mostly empty.

Fully Associative offers the most flexibility, in that all cache lines can be used. This is also the
most complex, because it uses a larger associative memory, which is complex and costly.

N–Way Set Associative is a mix of the two strategies. It uses a smaller (and simpler)
associative memory. Each cache line holds N = 2^K sets, each the size of a memory block.
Each cache line has N cache tags, one for each set.

Consider variations of mappings to store 256 memory blocks.

Direct Mapped Cache 256 cache lines

“1–Way Set Associative” 256 cache lines 1 set per line

2–Way Set Associative 128 cache lines 2 sets per line

4–Way Set Associative 64 cache lines 4 sets per line

8–Way Set Associative 32 cache lines 8 sets per line

16–Way Set Associative 16 cache lines 16 sets per line

32–Way Set Associative 8 cache lines 32 sets per line

64–Way Set Associative 4 cache lines 64 sets per line

128–Way Set Associative 2 cache lines 128 sets per line

256–Way Set Associative 1 cache line 256 sets per line

Fully Associative Cache 256 sets

N–Way Set Associative caches can be seen as a hybrid of the Direct Mapped Caches
and Fully Associative Caches. As N goes up, the performance of an N–Way Set Associative
cache improves. After about N = 8, the improvement is so slight as not to be worth the
additional cost.

Cache Memory in Modern Computer Systems

The above discussion of a single level cache attached to main memory is sufficient to illustrate
the main ideas behind cache memory. Modern computer systems have gone far beyond this
simple design. We now jump into reality.

Almost all modern computer systems have either a two–level (L1 and L2) or three–level
(L1, L2, and L3) cache system. Those that do not, such as the CPU for the IBM z/10, have a
four–level cache. Furthermore, all modern designs have a “split cache” for the level 1; there is
an I–cache and D–cache (Instruction Cache and Data Cache) at this level. In order to illustrate
the advantages of these designs, we assume the following two–level design, which is based on
the actual structure found in early Pentium designs.

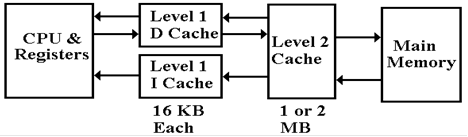
We now address two questions for this design before addressing the utility of a third level in the
cache. The first question is why the L1 cache is split into two parts. The second question is why
the cache has two levels. Suffice it to say that each design decision has been well validated by
empirical studies; we just give a rationale.

There are several reasons to have a split cache, either between the CPU and main memory or
between the CPU and a higher level of cache. One advantage is the “one way” nature of the L1
Instruction Cache; the CPU cannot write to it. This means that the I–Cache is simpler and faster
than the D–Cache; faster is always better. In addition, having the I–Cache provides some
security against self modifying code; it is difficult to change an instruction just fetched and write
it back to main memory. There is also slight security against execution of data; nothing read
through the D–Cache can be executed as an instruction.

The primary advantage of the split level–1 cache is support of a modern pipelined CPU. A
pipeline is more akin to a modern assembly line. Consider an assembly line in an auto plant.
There are many cars in various stages of completion on the same line. In the CPU pipeline, there
are many instructions (generally 5 to 12) in various stages of execution. Even in the simplest
design, it is almost always the case that the CPU will try to fetch an instruction in the same clock
cycle as it attempts to read data from memory or write data to memory.

Here is a schematic of the pipelined CPU for the MIPS computer [R007].

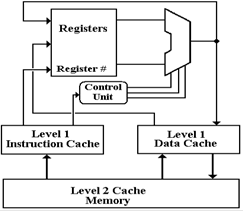This shows two of the five stages of the MIPS pipeline.
In any one clock period, the control unit will access the
Level 1 I–Cache and the ALU might access the L1
D–Cache. As the I–Cache and D–Cache are separate
memories, they can be accessed at the same time with
no conflict.

We note here that the ALU does not directly access the
D–Cache; it is the control unit either feeding data to a
register or writing the output from the ALU to primary
memory, through the D–Cache. The basic idea is sound:
two memory accesses per clock tick.

There is one slight objection possible to the split–cache design.
As we noted above, increasing
the hit rate on a cache memory results in faster access to the contents of both that cache and,
indirectly, the memory being served by that cache. It should be obvious that the cache hit rate is
lower for each of the smaller split L1 caches that it would be for a larger combined L1 cache.
Empirical data suggests that the advantage of simultaneous access to both instructions and data
easily overcomes the disadvantage of the slightly increased miss rate. Practical experience with
CPU design validates these empirical data.

The next question relates to the multiplicity of cache levels. Why have a 64–KB L1 cache and a
1–MB (1,024 KB) L2 cache in preference to a 1,092–KB unified cache. Here is an answer based
on data for the Apple iMAC G5, as reported in class lectures by David Patterson [R035]. The
access times and sizes for the various memory levels are as follows:

	Registers	L1 I–Cache	L1 D–Cache	L2 Cache	DRAM
Size	1 KB	64 KB	32 KB	512 KB	256 MB
Access Time	0.6 ns	1.9 ns	1.9 ns	6.9 ns	55 ns

The basic point is that smaller caches have faster access times. This, coupled with the principle
of locality implies that the two–level cache will have better performance than a larger unified
cache. Again, industrial practice has born this out.

The utility of a multi–level cache is illustrated by the following example, based on the
access times given in the previous table.
Suppose the following numbers for each of the three memory levels.
      L1 Cache            Access Time = 0.60 nanoseconds          Hit rate = 95%
      L2 Cache            Access Time = 1.90 nanoseconds          Hit rate = 98%
      Main Memory    Access Time = 55.0 nanoseconds.

The one–level cache would be implemented with the access time and hit rate of the L2
cache, as the one–level cache would be that size. The effective access time is thus:
T_E = 0.98·1.90 + (1 – 0.98)·55.0 = 0.98·1.90 + 0.02·55.0 = 1.862 + 1.10 = 2.972.

The two–level cache would use the L1 and L2 caches above and have access time:
T_E = 0.95·0.60 + (1 – 0.95)·[0.98·1.90 + (1 – 0.98)·55.0]
= 0.95·0.60 + 0.05·2.972 = 0.570 + 0.1486 = 0.719 nanoseconds.

The two–level cache system is about four times faster than the bigger unified cache.

Cache and Multi–Core Processors

The goal of every CPU design is to increase performance according to some type of relevant
benchmark. One way to do this is to increase the clock rate of the CPU. Another way to do this
is to add more cache memory on the CPU chip. As transistor densities increase, both options
appear to be appealing. There is, however, a problem with each of the options; as each increases,
the power density on the chip increases and the chip temperature climbs into a range not
compatible with stable operation.

One way to handle this heat problem is to devote more of the chip to cache memory and less to
computation. As noted by Stallings [R033], “Memory transistors are smaller and have a power
density an order of magnitude lower than logic. … the percentage of the chip area devoted to
memory has grown to exceed 50% as the chip transistor density has increased.”

Here is a diagram of a quad–core Intel Core i7 CPU. Each core has its own L1 caches as well
as dedicated L2 cache. The four cores share an 8–MB Level 3 cache.

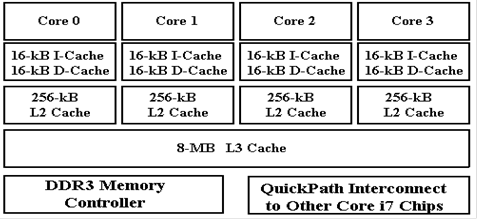
Figure: Intel Core i7 Block Diagram

Virtual Memory

We now turn to the next example of a memory hierarchy, one in which a magnetic disk normally
serves as a “backing store” for primary core memory. This is virtual memory. While many of
the details differ, the design strategy for virtual memory has much in common with that of cache
memory. In particular, VM is based on the idea of program locality.

Virtual memory has a precise definition and a definition implied by common usage. We discuss
both. Precisely speaking, virtual memory is a mechanism for translating logical addresses (as
issued by an executing program) into actual physical memory addresses. The address
translation circuitry is called a MMU (Memory Management Unit).

Description: ͥØ

This definition alone provides a great advantage to an Operating System, which can then
allocate processes to distinct physical memory locations according to some optimization. This
has implications for security; individual programs do not have direct access to physical memory.
This allows the OS to protect specific areas of memory from unauthorized access.

Virtual Memory in Practice

Although this is not the definition, virtual memory has always been implemented by pairing a
fast DRAM Main Memory with a bigger, slower “backing store”. Originally, this was magnetic
drum memory, but it soon became magnetic disk memory. Here again is the generic two–stage
memory diagram, this time focusing on virtual memory.

The invention of time–sharing operating systems introduced another variant of VM, now part
of the common definition. A program and its data could be “swapped out” to the disk to allow
another program to run, and then “swapped in” later to resume.

Virtual memory allows the program to have a logical address space much larger than the
computers physical address space. It maps logical addresses onto physical addresses and moves
“pages” of memory between disk and main memory to keep the program running.

An address space is the range of addresses, considered as unsigned integers, that can be
generated. An N–bit address can access 2^N items, with addresses 0 … 2^N – 1.

16–bit address 2¹⁶ items          0 to      65535
20–bit address 2²⁰ items          0 to      1,048,575
32–bit address 2³² items          0 to      4,294,967,295

In all modern applications, the physical address space is no larger than the logical address space.
It is often somewhat smaller than the logical address space. As examples, we use a number of
machines with 32–bit logical address spaces.

      Machine                           Physical Memory             Logical Address Space
      VAX–11/780                    16 MB                               4 GB (4, 096 MB)
      Pentium (2004)                 128 MB                             4 GB
      Desktop Pentium              512 MB                             4 GB
      Server Pentium                  4 GB                                 4 GB
      IBM z/10 Mainframe        384 GB                             2⁶⁴ bytes = 2³⁴ GB

Organization of Virtual Memory

Virtual memory is organized very much in the same way as cache memory. In particular, the
formula for effective access time for a two–level memory system (pages 381 and 382 of this text)
still applies. The dirty bit and valid bit are still used, with the same meaning. The names are
different, and the timings are quite different. When we speak of virtual memory, we use the
terms “page” and “page frame” rather than “memory block” and “cache line”. In the virtual
memory scenario, a page of the address space is copied from the disk and placed into an equally
sized page frame in main memory.

Another minor difference between standard cache memory and virtual memory is the way in
which the memory blocks are stored. In cache memory, both the tags and the data are stored in a
single fast memory called the cache. In virtual memory, each page is stored in main memory in a
place selected by the operating system, and the address recorded in a page table for use of the
program.

Here is an example based on a configuration that runs through this textbook. Consider a
computer with a 32–bit address space. This means that it can generate 32–bit logical addresses.
Suppose that the memory is byte addressable, and that there are 2²⁴ bytes of physical memory,
requiring 24 bits to address. The logical address is divided as follows:

Bits	31 – 28	27 – 24	23 – 20	19 – 16	15 – 12	11 – 8	7 – 4	3 – 0
Field	Page Number					Offset in Page

The physical address associated with the page frame in main memory is organized as follows

Bits	23 – 20	19 – 16	15 – 12	11 – 8	7 – 4	3 – 0
Field	Address Tag			Offset in Page Frame

Virtual memory uses the page table to translate virtual addresses into physical addresses. In
most systems, there is one page table per process. Conceptually, the page table is an array,
indexed by page frame of the address tags associated with each process. But note that such an
array can be larger than the main memory itself. In our example, each address tag is a
12–bit value, requiring two bytes to store, as the architecture cannot access fractional bytes. The
page number is a 20–bit number, from 0 through 1,048,575. The full page table would require
two megabytes of memory to store.

Each process on a computer will be allocated a small page table containing mappings for the
most recently used logical addresses. Each table entry contains the following information:

1. The valid bit, which indicates whether or not there is a valid address tag (physical
page number) present in that entry of the page table.

2. The dirty bit, indicating whether or not the data in the referenced page frame
has been altered by the CPU. This is important for page replacement policies.

3. The 20–bit page number from the logical address, indicating what logical page
is being stored in the referenced page frame.

4. The 12–bit unsigned number representing the address tag (physical page number).

More on Virtual Memory: Can It Work?

Consider again the virtual memory system just discussed. Each memory reference is based on
a logical address, and must access the page table for translation.

But wait! The page table is in memory.
Does this imply two memory accesses for each memory reference?

This is where the TLB (Translation Look–aside Buffer) comes in. It is a cache for a page
table, more accurately called the “Translation Cache”.

The TLB is usually implemented as a split associative cache.
One associative cache for instruction pages, and
One associative cache for data pages.

A page table entry in main memory is accessed only if the TLB has a miss.

The Complete Page Table Structure

All page tables are under the control of the Operating System, which creates a page table for
each process that is loaded into memory. The computer hardware will provide a single register,
possibly called PTA (Page Table Address) that contains the address of the page table for each
process, along with other information.

Each page table, both the master table and each process table, has contents that vary depending
on the value in the valid bit.
If Valid = 1, the contents are the 12–bit address tag.
If Valid = 0, the contents are the disk address of the page as stored on disk.

As the above implies, the page table for a given process may be itself virtualized; that is
mostly stored in virtual memory. Only a small part of a processes full page table must be in
physical memory for fast access. Of that, a smaller part is in the TLB for faster access.

Virtual Memory with Cache Memory

Any modern computer supports both virtual memory and cache memory. We now consider
the interaction between the two.

The following example will illustrate the interactions. Consider a computer with a 32–bit
address space. This means that it can generate 32–bit logical addresses. Suppose that the
memory is byte addressable, and that there are 2²⁴ bytes of physical memory, requiring 24 bits
to address. The logical address is divided as follows:

Bits	31 – 28	27 – 24	23 – 20	19 – 16	15 – 12	11 – 8	7 – 4	3 – 0
Field	Page Number					Offset in Page

We suppose further that virtual memory implemented using page sizes of 2¹² = 4096 bytes, and
that cache memory implemented using a fully associative cache with cache line size of 16 bytes.
The physical address is divided as follows:

Bits	23 – 20	19 – 16	15 – 12	11 – 8	7 – 4	3 – 0
Field	Memory Tag					Offset

Consider a memory access, using the virtual memory. Conceptually, this is a two–step process.
First, the logical address is mapped into a physical address using the virtual memory system.
Then the physical address is sent to the cache system to determine whether or not there is a cache
hit.

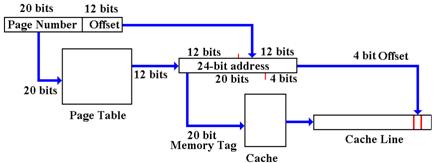
Description: "Ø

Figure: Two–Stage Virtual Address Translation

The Virtually Mapped Cache

One solution to the inefficiencies of the above process is to use a virtually mapped cache. In
our example we would use the high order 28 bits as a virtual tag. If the addressed item is in the
cache, it is found immediately.

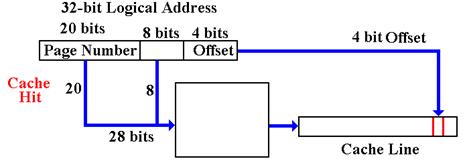
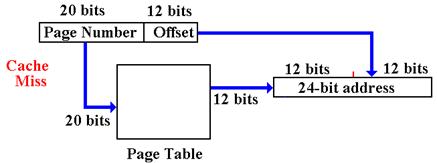
Description: à

A Cache Miss accesses the Virtual Memory system.

Description: à

The Problem of Memory Aliasing

While the virtually mapped cache presents many advantages, it does have one notable drawback
when used in a multiprogramming environment. In such an environment, a computer might be
simultaneously executing more than one program. In the real sense, only one program at a time
is allocated to any CPU. Thus, we might have what used to be called “time sharing”, in which
a CPU executes a number of programs in sequence.

There is a provision in such a system for two or more cooperating processes to request use of the
same physical memory space as a mechanism for communication. If two or more processes have
access to the same physical page frame, this is called memory aliasing. In such scenarios,
simple VM management systems will fail. This problem can be handled, as long as one is aware
of it.

The topic of virtual memory is worthy of considerable study. Mostly it is found in a course on
Operating Systems. The reader is encouraged to consult any one of the large number of
excellent textbooks on the subject for a more thorough examination of virtual memory.