Handling of
Arrays, Strings and Other Data Structures
Up to this point, we have
studied simple data types and basic arrays
built on those simple data types.
Some of
the simple data types studied include.
a) Integers:
both halfword and fullword.
b) Packed
decimal
c) Character
data.
This
lecture will cover the following:
1. A
generalized “self describing” array that includes limits on the
permitted index values. Only 1–D and 2–D arrays will be considered.
2. Options
for a string data type and how that differs from a character array.
3. Use
of indirect addressing with pointer structures generalized to
include descriptions of the data
item pointed to.
Structures
of Arrays
We first
consider the problem of converting an
array into an byte displacement.
We then
consider two ways of organizing a two–dimensional array, and
proceed to convert the
The
simple array type has two variants:
0–based: The
first element in the array is either AR[0] for a
singly
dimensioned array or
AR[0][0] for a 2–D array.
1–based: The
first element in the array is either AR[1] for a
singly
dimensioned array or
AR[1][1] for a 2–D array.
We shall
follow the convention of using only 0–based arrays.
One reason
is that it allows for efficient conversion from a set of
into a displacement from the base address.
By
definition, the base address of an array will be the address of its first
element: either the address of AR[0] or AR[0][0].
Byte Displacement
and Addressing Array Elements
The General
Case
We first
consider addressing issues for an array that contains either character
halfword, or fullword data. It will be
constrained to one of these types.
The
addressing issue is well illustrated for a singly dimensioned array.
|
Byte |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Characters |
C[0] |
C[1] |
C[2] |
C[3] |
C[4] |
C[5] |
C[6] |
C[7] |
C[8] |
C[9] |
C[10] |
C[11] |
|
Halfwords |
HW[0] |
HW[1] |
HW[2] |
HW[3] |
HW[4] |
HW[5] |
||||||
|
Fullwords |
FW[0] |
FW[1] |
FW[2] |
|||||||||
For each
of these examples, suppose that the array begins at address X.
In other
words, the address declared for the array is that of its element 0.
The
character entries would be: C[0] at X, C[1] at X + 1,
C[2] at X + 2, etc.
The
halfword entries would be: HW[0] at X, HW[1] at X + 2,
etc.
The fullword
entries would be: FW[0] at X, FW[1] at X + 4, etc.
Byte
Displacement and Addressing Array Elements
Our Case
I have
decided not to write macros that handle the general case, but to
concentrate on arrays that store 4–byte fullwords.
The goal
is to focus on array handling and not macro writing.
The data
structure for such an array will be designed under
the following considerations.
1. It
must have a descriptor specifying the maximum allowable
In this data structure, I store
the size and derive the maximum
2. It
might store a descriptor specifying the minimum allowable
For a 0–based array, that
3. It
should be created by a macro that allows the size to be specified
at assembly time. Once specified, the array size will not
change.
What Do We
Need to Know About a 1–D Array?
Here, I
assume the following:
1. The
array is statically allocated; once loaded, its size is set.
2. The
array is “zero based”; its first element has index 0.
I decide to include this “base value”
in the array declaration, just
to show how to do it.
3. The
array is self–describing for its maximum size.
Here is
an example of the proposed data structure as it would be written
in System 370 Assembler. The array is
named “ARRAY”.
ARBASE DC F‘0’ THE
FIRST
ARSIZE DC F‘100’
SIZE OF THE ARRAY
ARRAY DC 100F‘0’ STORAGE FOR THE ARRAY
I want to generalize this to allow for a macro
construction that will specify
both the array name and its size.
The
Constructor for a One–Dimensional Array
Here is
the macro I used to construct a one–dimensional array
while following the design considerations listed above.
33 MACRO
34 &L1 ARMAKE
&NAME,&SIZE
35
&L1 B X&SYSNDX
36
&NAME.B DC
F'0' ZERO BASED ARRAY
37
&NAME.S DC
F'&SIZE'
38
&NAME.V DC
&SIZE.F'0'
39
X&SYSNDX
40 MEND
Line
34: The macro is named “ARMAKE” for “Array
Make”.
It takes two arguments:
the array name and array size.
A typical invocation: ARMAKE XX,20 creates an
array called XX.
Note the “&L1” on line 34 and repeated on line 35. This allows a
macro
definition to be given a
More on the
1–D Constructor
33 MACRO
34
&L1 ARMAKE &NAME,&SIZE
35 &L1 B
X&SYSNDX
36 &NAME.B
DC F'0' ZERO BASED ARRAY
37 &NAME.S
DC F'&SIZE'
38
&NAME.V DC
&SIZE.F'0'
39
X&SYSNDX
40 MEND
Line
35: A macro is used to generate a code
sequence. Since I am using it
to create a data
structure, I must provide code to jump around the
data, so that the data
will not be executed.
While it might be possible to
place all invocations of this macro
in a program location
that will not be executed, I do not assume that.
Line
36: I put in the lower bound on the
declaration might look
like.
Line 37 This
holds the size of the array.
Label
Concatenations in the Constructor
33 MACRO
34
&L1 ARMAKE &NAME,&SIZE
35
&L1 B X&SYSNDX
36 &NAME.B
DC F'0' ZERO BASED
ARRAY
37 &NAME.S
DC F'&SIZE'
38 &NAME.V
DC &SIZE.F'0'
39 X&SYSNDX
40 MEND
Recall
that the system variable symbol &SYSNDX in a counter that contains
a four digit number unique to the macro expansion.
Line 39
uses one style of concatenation to produce a unique
Suppose
that this is the third macro expansion; the
Lines
36, 37, and 38 use another type of concatenation, based on the dot.
If &NAME is XX, then
the
Sample
Expansions of the 1–D Constructor Macro
90 ARMAKE XX,20
000014
47F0 C06A 00070 91+
B X0003
000018
00000000 92+XXB DC F'0'
00001C
00000014 93+XXS DC F'20'
000020
0000000000000000 94+XXV DC 20F'0'
000070
8B30 0000 00000 95+X0003
96 ARMAKE YY,40
000074
47F0 C11A 00120 97+
B X0004
000078
00000000 98+YYB DC
F'0'
00007C
00000028 99+YYS DC F'40'
000080
0000000000000000 100+YYV DC 40F'0'
000120
8B30 0000 00000 101+X0004
Notice
the
Two More
Macros for 1–D Arrays
I now
define two macros to use the data structure defined above.
I call
these ARPUT
and ARGET. Each will use R4 as a working register.
Macro ARPUT &NAME,&INDX stores
the contents of register R4
into the
Consider
the high–level language statement A2[10]
= Y.
This
becomes L R4,Y
ARPUT A2,=F‘10’ GET ELEMENT
10
Consider
the high–level language statement Y
= A3[20].
This
becomes ARGET A3,=F‘20’ CHANGE ELEMENT 20
ST R4,Y
NOTE: For some reason, I decided to implement the
when I wrote the code. I just continue the practice in this slide.
Design of
the Macros
The two
macros, ARPUT
and ARGET,
share much of the same design.
Much is
centered on proper handling of the
fullword. It would probably make more
sense to use a halfword for the
Here are
the
1. The
2. If
the value in the
array, the macro exits. For N elements, valid
3. Using
the
in order to get a byte offset
from the base address.
4. ARPUT stores the value
in R4 into the
ARGET retrieves the value at the
The ARPUT
Macro
Here is
the macro definition.
44 MACRO
45
&L2 ARPUT &NAME,&INDX
46
&
47 L
R3,&INDX
48 C
R3,&NAME.B
49 BL
Z&SYSNDX
50 C
R3,&NAME.S
51 BNL
Z&SYSNDX
52
53 ST
R4,&NAME.V(R3)
54 B
Z&SYSNDX
55
S&SYSNDX DC F'0'
56
Z&SYSNDX L R3,S&SYSNDX
57 MEND
Note the
two
with the System Variable Symbol &SYSNDX.
This
allows the macro to use conditional branching.
ARPUT
Expanded
Here is
an invocation of ARPUT and its expansion.
107 ARPUT XX,=F'10'
000126
5030 C146 0014C 108+
ST R3,S0005
00012A
5830 C46A 00470 109+
L R3,=F'10'
00012E
5930 C012 00018 110+
C R3,XXB
000132
4740 C14A 00150 111+
BL Z0005
000136
5930 C016 0001C 112+
C R3,XXS
00013A
47B0 C14A 00150 113+
BNL Z0005
00013E
8B30 0002 00002 114+
000142
5043 C01A 00020 115+
ST R4,XXV(R3)
000146
47F0 C14A 00150 116+
B Z0005
00014A
0000
00014C
00000000 117+S0005
DC F'0'
000150
5830 C146 0014C 118+Z0005 L
R3,S0005
Note the
labels generated by use of the System Variable Symbol &SYSNDX.
Actions for
This Macro Invocation
We now
examine the actions of the macro ARPUT.
108+ ST
R3,S0005
Register
R3 will be used to hold the
the value so that it can be restored at the end of the macro.
109+ L
R3,=F'10'
Register
R3 is loaded with the
As the
is copied in the macro expansion.
ARPUT:
Checking the
The
value of the array
110+ C R3,XXB
111+ BL Z0005
112+ C R3,XXS
113+ BNL Z0005
This
code checks that the
The
requirement is that XXB Ł
If this
is not met, the macro restores the value of R3 and exits.
If the
requirement is met, the
in order to convert it into a byte displacement from element 0.
114+
ARPUT:
Storing the Value
Here is
the code to store the value into the array, called XXV.
115+ ST
R4,XXV(R3)
116+ B Z0005
117+S0005 DC
F'0'
118+Z0005 L
R3,S0005
Line
115 This is the actual store command.
Line
116 Note the necessity of branching
around the stored value,
so that the data will not
be executed as if it were code.
Line
117 The save area for the macro.
Line
118 This restores the original value of
R3, the register
used to hold the
The ARGET
Macro
Here is
the macro definition.
61 MACRO
62
&L3 ARGET &NAME,&INDX
63
&
64 L
R3,&INDX
65 C
R3,&NAME.B
66 BL
Z&SYSNDX
67 C
R3,&NAME.S
68 BNL
Z&SYSNDX
69
70 L
R4,&NAME.V(R3)
71 B
Z&SYSNDX
72
S&SYSNDX DC F'0'
73
Z&SYSNDX L R3,S&SYSNDX
74 MEND
ARGET
Expanded
Here is
an invocation of the macro and its expansion.
119 ARGET YY,=F'20'
000154
5030 C172 00178 120+
ST R3,S0006
000158
5830 C46E 00474 121+
L R3,=F'20'
00015C
5930 C072 00078 122+
C R3,YYB
000160
4740 C176 0017C 123+
BL Z0006
000164
5930 C076 0007C 124+
C R3,YYS
000168
47B0 C176 0017C 125+
BNL Z0006
00016C
8B30 0002 00002 126+
000170
5843 C07A 00080 127+
L R4,YYV(R3)
000174
47F0 C176 0017C 128+
B Z0006
000178
00000000 129+S0006
DC F'0'
00017C
5830 C172 00178 130+Z0006 L
R3,S0006
The only
difference between this macro and ARPUT occurs in line 127
of the expansion. Here the value is
loaded into register R4.
Row–Major
and
The
mapping of a one–dimensional array to linear address space is simple.
How do
we map a two–dimensional array? There
are three standard options.
Two are called row–major and column–major order.
Consider
the array declared as INT A[2][3], using 32–bit integers.
In this
array the first
Suppose
the first element is found at address A.
The following table shows
the allocation of these elements to the linear address space.
|
Address |
Row Major |
Column
Major |
|
A |
A[0][0] |
A[0][0] |
|
A + 4 |
A[0][1] |
A[1][0] |
|
A + 8 |
A[0][2] |
A[0][1] |
|
A + 12 |
A[1][0] |
A[1][1] |
|
A + 16 |
A[1][1] |
A[0][2] |
|
A + 20 |
A[1][2] |
A[1][2] |
The mechanism for Java arrays is likely to be somewhat
different.
Addressing
Elements in Arrays of 32–Bit Fullwords
Consider
first a singly dimensioned array that holds 4–byte fullwords.
The addressing is simple.
Address ( A[K] ) = Address (
A[0] ) + 4·K.
Suppose
that we have a two dimensional array declared as A[M][N],
where each of M and N has a fixed positive integer value.
Again,
we assume 0–based arrays and ask for the address of an element
A[K][J], assuming that 0 Ł K < M and 0 Ł J
< N.
At this
point, I must specify either row–major or column–major ordering.
As
FORTRAN is the only major language to use column–major ordering,
I shall assume row–major. The formula is
as follows.
Element
offset = K·N + J, which leads to
Address
(A[K][J]) = Address (A[0][0]) + 4·(K·N + J)
Example:
Declare A[2][3]
Suppose
that element A[0][0] is at address A.
Address
(A[K][J]) = Address (A[0][0]) + 4·(K·3 + J).
Element A[0][0] is at offset 4·(0·3 + 0) = 0, or address A + 0.
Element A[0][1] is at offset 4·(0·3 + 1) = 4, or address A + 4.
Element A[0][2] is at offset 4·(0·3 + 2) = 8, or address A + 8.
Element A[1][0] is at offset 4·(1·3 + 0) = 12, or address A + 12.
Element A[1][1] is at offset 4·(1·3 + 1) = 16, or address A + 16.
Element A[1][2] is at offset 4·(1·3 + 1) = 20, or address A + 20.
2–D Arrays:
An Example Data Structure
Here is
a first cut at what we might want the data structure to look like.
ARRB DC F‘0’ ROW
ARRCNT DC F‘30’
NUMBER OF ROWS
ARCB DC F‘0’
ARCCNT DC F‘20’
NUMBER OF
ARRAY DC 600F‘0’ STORAGE FOR THE ARRAY
NOTE: The number 600
in the declaration of the storage for the array
is not
It is the product of the row and
column count.
We need
a way to replace the number 600 by 30·20,
size of the array is a computed value.
This
leads us to the Macro feature called “SET Symbols”.
SET Symbols
The
feature called “SET Symbols” allows for computing values in a macro,
based on the values or attributes of the symbolic parameters.
There
are three basic types of SET symbols.
1. Arithmetic These are 32–bit numeric values, initialized
to 0.
2. Binary These are 1–bit values, initialized to
0.
3. Character These are strings of characters, initialized
to the null string.
Each of
these comes in two varieties: Local and Global.
The local SET symbols have meaning only
within the macro in which
they are defined. Declarations in
different macro expansions are
The global SET symbols specify values that
are to be known in other macro
expansions within the same assembly.
A proper
use of a global SET symbol demands the use of conditional assembly
to insure that the symbol is defined once and only once.
Local and
Global Set Declarations
Here are
the instructions used to declare the SET symbols.
|
Type |
Local |
Global |
||
|
|
Instruction |
Example |
Instruction |
Example |
|
Arithmetic |
LCLA |
LCLA &F1 |
GBLA |
GBLA &G1 |
|
Binary |
LCLB |
LCLB &F2 |
GBLB |
GBLB &G2 |
|
Character |
LCLC |
LCLC &F3 |
GBLC |
GBLC &G3 |
Each of
these instructions declares a SET symbol that can have its value
assigned by one of the SET instructions.
There are three SET instructions.
SETA SET
Arithmetic Use with LCLA or GBLA
SET symbols.
SETB SET
Binary Use with LCLB or
GBLB SET symbols.
Placing the
Conditional Assembly Instructions
The
requirements for placement of these instructions depend on the Operating
System being run. The following
standards have two advantages:
1. They
are the preferred practice for clear programming, and
2. They
seem to be accepted by every version of the Operating System.
Here is
the sequence of declarations.
1. The
macro prototype statement.
2. The
global declarations used: GBLA, GBLB, or GBLC
3. The
local declarations used: LCLA, LCLB, or
LCLC
4. The
appropriate SET instructions to give values to the SET symbols
5. The
macro body.
Example of
the Preferred Sequence
The
following silly macro is not even complete.
It illustrates the sequence
for declaration, but might be incorrect in some details.
MACRO
&
GBLC &DATES HOLDS THE DATE
GBLB &DATEP HAS DATES BEEN DEFINED
LCLA &LEN, &MID
AIF (&DATEP).N20 IS DATE DEFINED?
&DATES DC C‘&SYSDATE’ SET THE DATE
&DATEP SETB (1) DECLARE IT SET
.N20 ANOP
&LEN SETA L’&HEAD LENGTH OF THE HEADER
&MID SETA (120-&LEN)/2 MID
&
A
Constructor Macro for the 2–D Array
This
macro uses one arithmetic SET symbol to calculate the array size.
This has no line numbers because it has yet to be tested by assembling it.
MACRO
&L1 ARMAK2D &NAME,&ROWS,&COLS
LCLA
&SIZE
&SIZE SETA (&ROWS*&COLS)
&L1 B X&SYSNDX
&NAME.RB DC
F'0' ROW INDEX
&NAME.RS DC F'&ROWS'
&NAME.CB DC
F'0'
&NAME.CS DC
F'&COLS'
&NAME.V DC
&SIZE.F'0'
X&SYSNDX
MEND
Strings vs.
Arrays of Characters
While a
string may be considered an array of characters, this
is not the normal practice.
A string
is a sequence of characters with a fixed length.
A string
is stored in “string space”, which
may be considered to be
a large dynamically allocated array that contains all of the strings used.
There
are two ways to declare the length of a string.
1. Allot
a special “end of string” character, such as the character with
code X‘00’, as done in C and C++.
2. Store
an explicit string length code, usually as a single byte that
prefixes the string. A single byte can store an unsigned integer
in
the range 0 through 255
inclusive.
In this method, the maximum string
length is 255 characters.
There
are variants on these two methods; some are worth consideration.
Example
String
In this
example, I used strings of digits that are encoded in EBCDIC.
The
character sequence “12345” would be encoded as F1 F2 F3 F4 F5.
This is
a sequence of five characters. In either
of the above methods, it
would require six bytes to be stored.
Here is
the string, as would be stored by C++.
|
Byte number |
0 |
1 |
2 |
3 |
4 |
5 |
|
Contents |
F1 |
F2 |
F3 |
F4 |
F5 |
00 |
Here is
the string, as would be stored by Visual Basic Version 6.
|
Byte number |
0 |
1 |
2 |
3 |
4 |
5 |
|
Contents |
05 |
F1 |
F2 |
F3 |
F4 |
F5 |
Each
method has its advantages. The main
difficulty with the first approach,
as it is implemented in C and C++, is that the programmer is responsible for
the terminating X‘00’. Failing to
place it leads to strange run–time errors.
Sharing String
Space
String
variables usually are just pointers into string space.
Consider the following example in the style of Visual Basic.
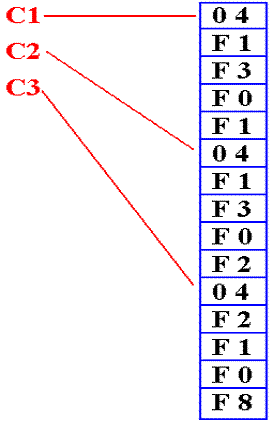Here, each of the symbols C1, C2, and C3
references a string of length 4.
C1
references the string “1301”
C2
references the string “1302”
C3
references the string “2108”
Using
Another
string storage method uses
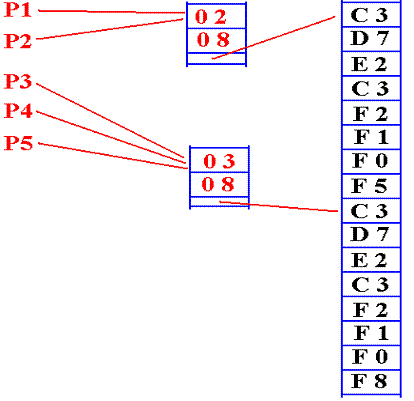Here the intermediate node has the
following structure.
1. A
reference count
2. The string length
3. A pointer into string space.
There
are two references to the first
string, of length 8: “CPSC 2105”.
There
are three references to the second
string, also of length 8: “CPSC 2108”.
There
are many advantages to this method of
stored in the intermediate node. It is
likely the method used by Java.