NUMIN: A Program to Input Binary Integers

Numeric data are input into a computer in a three step process.

1. The data are read in as a sequence of characters.

For the IBM System/360, the characters are encoded as EBCDIC.

2. The data are converted to the proper form for numeric use.

3. The data are stored, either in memory or general–purpose registers,
for use in computations.

We shall focus on the input of integer data to be stored in one of the
general–purpose registers.

As an arbitrary constraint, we shall limit the numbers to 9 digits,
though the numbers are allowed to be smaller.

Note that any possible nine–digit integer can be stored as a 32–bit fullword.

NUMIN: The Scenario

Remember that input should be viewed as a card image of 80 columns.

Consider a field of N characters found beginning in column M.

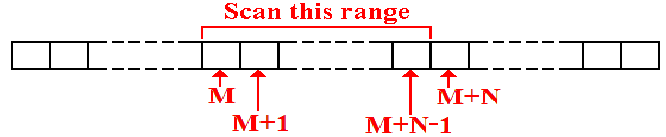
Suppose that the leftmost byte in this array is associated with the label CARDIN.

The leftmost byte in the range of interest will be denoted by the label CARDIN+M.

Elements in this range will be referenced using an index register as CARDIN+M(Reg).

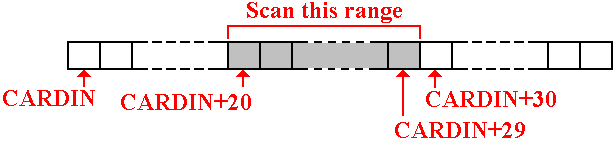
Our specific example will assume the following:

1. The character field to hold the integer occupies ten columns on the card,
beginning in column 20 and running through column 29.

2. The number is right justified. If negative, the number has a leading minus sign.

3 An entirely blank field is accepted as representing the number zero.

NUMIN: The Standard Approach

We begin this set of notes by recalling a more standard approach to conversion
from a sequence of EBCDIC characters to a binary number in a register.

This sample code will assume that all numbers are non–negative.

Here are some data declarations that are used in the code.

* THE CHARACTERS FOR INPUT ARE FOUND BEGINNING

* AT CARDIN+20 THROUGH CARDIN+29. NO MINUS SIGN.

DIGITSIN DS CL10 TEN BYTES TO HOLD 10 CHARACTERS

PACKEDIN DS PL6 SIX BYTES HOLD 11 DIGITS

PACKDBL DS D DOUBLE WORD TO HOLD PACKED

Here is the code that uses the above data structures.

MVC DIGITSIN(10),CARDIN+20 GET 10 CHARACTERS

PACK PACKEDIN,DIGITSIN CONVERT TO PACKED

ZAP PACKDBL,PACKEDIN FORMAT FOR CVB

CVB R5,PACKDBL BINARY INTO R5.

NUMIN: The Strategy

The figure below shows the part of the 80–column card image
that contains the digits to be interpreted.

The algorithm works as follows:

1. It initializes an output register to 0. Arbitrarily, I choose R7.

2. It scans left to right, looking for a nonblank character.

Assuming that a nonblank character is found in this field, it does the following.

3. If the character is a minus sign, set a flag that the number is negative
and continue the scan.

4. If the number is a digit, process it. If not a digit or “–”, ignore it.

NUMIN: EXAMPLE

Consider processing the number represented by the digit string “9413”.

We shall illustrate the process used by our conversion routine.

In this example, let N be the value of the number,

D be the digit read in, and

V be the numeric value of that digit.

Start with N = 0.

Read in D = “9”. Convert to V = 9. N = N·10 + V = 0·10 + 9 = 9

Read in D = “4”. Convert to V = 4. N = N·10 + V = 9·10 + 4 = 94

Read in D = “1”. Convert to V = 1. N = N·10 + V = 94·10 + 1 = 941

Read in D = “3”. Convert to V = 3. N = N·10 + V = 941·10 + 3 = 9413

The integer value of this string is 9413.

Two New Instructions: LCR and IC

The code below will use two instructions that have not yet been discussed.

LCR (Load Complement Register)

Example LCR R1,R2

This loads register R1 with the negative (two’s–complement) of the
value in register R2.

IC (Insert Character)

Example IC R8,CARDIN+20(R3) GET THE DIGIT

This inserts the eight bits of the EBCDIC character into the low order 8 bits
(bits 24 – 31) of the destination register. The other bits are not changed.

Placing the Numerical Value of a Digit in a Register

The first thing to do is get the EBCDIC code into the register. My solution:

SR R8,R8 CLEAR R8

IC R8,CARDIN+20(R3) GET THE DIGIT

S R8,=X‘F0’ CONVERT TO VALUE OF DIGIT

In order to be sure that register R8 contains the EBCDIC code for the digit,
I first clear the register to zero and then move the character.

This step guarantees that bits 0 –23 of the register are 0 and that the value in
the register, taken as a 32–bit fullword, is the EBCDIC code for the digit.

I then subtract the value of the EBCDIC code for ‘0’ to get the value of the digit.

Another way to do this is load the register and use the logical instruction, with
mnemonic N, to mask out all but the last hexadecimal digit. Here is the code.

IC R8,CARDIN+20(R3) GET THE DIGIT

N R8,=X‘F’

NUMIN: Part 1

I now present my algorithm in fragments of code. We start with the beginning
code. Each fragment will be listed along with its associated data declarations.

This first code fragment just clears the result registers and checks to see if the
input field, in the ten columns beginning at CARDIN+20 is all blanks.

If it is all blanks, the routine equates that to 0 and returns.

NUMIN SR R7,R7 SET R7, THE RESULT, TO 0

SR R6,R6 CLEAR HIGH-ORDER PRODUCT

MVI THESIGN,C‘P’ DEFAULT TO POSITIVE

CLC CARDIN+20(10),SPACE10 IS THE INPUT ALL BLANKS

BE DONE IF SO, JUST EXIT WITH

* THE VALUE SET TO 0.

* MORE CODE HERE

* 0123456789 BE SURE OF THE COUNT BELOW

SPACE10 DC CL‘ ’ JUST TEN SPACES

THESIGN DS CL1

NUMIN: Part 2

* NOW SCAN LEFT TO RIGHT TO FIND FIRST NON-BLANK.

* USE BXLE WITH REGISTER PAIR (R4,R5).

SR R3,R3 CLEAR INDEX USED TO SCAN

* THE INPUT CHARACTER ARRAY

LA R4,1 SET INCREMENT TO 1

LA R5,9 OFFSET 9 IS THE LAST DIGIT

SCAN1 CLI CARDIN+20(R3),C‘ ’ DO WE HAVE A SPACE?

BNE NOTBLANK NO, IT MAY BE A DIGIT

BXLE R3,R4,SCAN1 ITS BLANK. LOOK AT NEXT

B DONE ALL BLANKS, WE ARE DONE

This scans left to right looking for a non–blank character, which should be there.
If none is found, it just quits. Admittedly, this should not happen, as we have
tested and found at least one non–blank character in the input.

NUMIN: Part 3

* AT THIS POINT, R3 IS THE INDEX OF THE NON-BLANK

* CHARACTER. THE VALUES IN (R4,R5) ARE STILL VALID.

* IN PARTICULAR R4 STILL HAS VALUE 1.

NOTBLANK CLI CARDIN+20(R3),C‘-’ DO WE HAVE A MINUS SIGN?

BNE ISDIG

MVI THESIGN,C‘N’ NOTE THE SIGN AS NEGATIVE

AR R3,R4 ADD 1 TO VALUE IN R3.

CR R3,R5 R3 HAS BEEN INCREMENTED

BH DONE QUIT IF IT IS TOO BIG.

If the first non–blank character is a minus sign, the sets a flag, which would be
a Boolean in a high–level language. Here it is just the character “N”.

If the first non–blank character is a minus sign, then the next character is assumed to be
the first digit. The index value is incremented by 1 to address the character after the “–”.

If the first non–blank character is not a minus sign, it is assumed to be a digit and
processed as one. Note however that the processing loop explicitly makes two tests
and processes the character only if it is not less than “0’ and not greater than “9”.

NUMIN: Part 4

At this point, we know that CARDIN+20(R3) references a non–blank character that
is in the range of card columns that might contain a digit. Here is the conversion loop.

ISDIG CLI CARDIN+20(R3),C‘0’ IS IT A DIGIT

BL LOOP NO – CODE < ‘0’

CLI CARDIN+20(R3),C‘9’ ANOTHER CHECK

BH LOOP NO – CODE > ‘9’

M R6,=F‘10’ MULTIPLY (R6,R7) BY 10

SR R8,R8 CLEAR R8

IC R8,CARDIN+20(R3) GET THE DIGIT

S R8,=X‘F0’ CONVERT TO VALUE OF DIGIT

AR R7,R8 ADD TO THE PRODUCT

LOOP BXLE R3,R4,ISDIG END OF THE LOOP

CLI THESIGN,C‘N’ WAS THE INPUT NEGATIVE

BNE DONE IT IS NOT NEGATIVE

LCR R7,R7 TAKE 2’S COMPLEMENT

DONE * HERE R7 CONTAINS THE BINARY VALUE