Declaring Binary Storage

There are many ways to declare binary storage. The four most useful are

1. B Ordinary binary,

2. F Full–word (32–bit binary two’s–complement integer),

3. H Half–word (16–bit) binary two’s–complement integer), and

4. X Hexadecimal.

Each of the B and X declarations may declare a storage area with length
from 1 through 256 bytes.

The lengths of the F and H declarations are fixed at 4 and 2 bytes respectively.
Apparently, it is possible to assign a length in bytes to either type, but this is strange.

Note that the two declarations below have an identical effect.

Each defines a 32–bit binary integer with value equal to 14,336 in decimal.

F1 DC F‘14336’ DEFAULT SIZE IS FOUR BYTES.

X1 DC XL4‘00003800’ SIZE SPECIFIED AS FOUR BYTES.

While the second declaration is unusual for a full–word, it makes some examples easier.

More On DC (Define Constant)

The general format of the DC statement is as follows.

Name

DC

dTLn ‘constant’

The name is an optional entry, but required if the program is to refer to
the field by name. The standard column positions apply here.

The declarative, DC, comes next in its standard position.

The entry “dTLn” is read as follows.

d is the optional duplication factor. If not specified, it defaults to 1.

T is the required type specification. The types for binary are B, F, H, and X.
Note that the data actually stored at the location does not need to be
of this type, but it is a good idea to restrict it to that type.

L is an optional length of the data field in bytes.

The ‘constant’ entry is required and is used to specify a value.
If the length attribute is omitted, the length is specified implicitly by this entry.

Again, it is rarely desirable to specify a length for the F and H data types.

Alignment and Value Ranges

Remember that the System/360 is a byte–addressable machine.

The type F declares a full–word, which is a four–byte field aligned on a
full–word boundary; i.e., its address is a multiple of four.

The type H declares a half–word, which is a two–byte field aligned on a
half–word boundary; i.e., its address is a multiple of two.

The ranges are what would be expected for standard two’s–complement arithmetic.

Type Bits Minimum Maximum Minimum Maximum

Half–word 16 –(2¹⁵) (2¹⁵) – 1 –32,768 32,767

Full–word 32 –(2³¹) (2³¹) – 1 –2,147,483,648 2,147,483,647

If the value declared in either a type F or type H constant is greater than that
allowed by the data type, the assembler merely truncates the leftmost digits.

Consider the following example

BAD DC H‘73728’ IN HEXADECIMAL, X‘12000’

This is truncated to a value of 8,192, which is X‘2000’. The leading 1 is dropped
from the hexadecimal representation, because only the last four digits fit into the
half–word storage allocation; 4 hexadecimal digits = 2 bytes = 1 half–word.

Sequential Memory

Consider the following two declarations which are sequential. Each is a half–word,
that is declared using the hexadecimal construct to make the example clear.

H1 DC XL2‘0102’ DECIMAL 258

H2 DC XL2‘0304’ DECIMAL 772

The half–word value stored at address H1 is decimal 258.

The full–word value stored at address H1 is hexadecimal 01020304, or 16, 909, 060.

This fact can present problems for the incautious coder.

To load the value of the half–word at address H1 into a register, one uses the
Load Half–word instruction; e.g., LH R4,H1. Register R4 gets 258.

But if I accidentally write a full–word load instruction, as in L R4,H1,
then register R4 will get the decimal value 16, 909, 060.

Similarly, suppose I declare a full–word as follows.

F1 DC XL4 ‘11121314’ DECIMAL 17,899,828

If the code says LH R4,F1, then F1 gets hexadecimal X‘1112’ or decimal 4370.

Binary Constants and Hexadecimal Constants

The type B declaration uses binary numbers (0 or 1) to define a string of bits.

The type X declaration uses hexadecimal digits to define what is also just
a string of bits.

Consider the following pairs of declarations.

B1 DC B‘10101110’

X1 DC XL1‘AE’ READ AS 1010 1110

B2 DC B‘0001001000010011’

X2 DC XL2‘1213’ READ AS 0001 0010 0001 0011

B1 and X1 each declare the same bit pattern.

B2 and X2 each declare the same bit pattern.

Personally, I find the hexadecimal constants much easier to read,
and would suggest not using the B declaration.

The most common use for the binary declaration would be to set bit patterns to be
sent to registers that control Input/Output devices. In standard programming, we
do not have access to those registers on a System/360.

Input and Output of Binary Data

All data are input originally as EBCDIC characters.

All data printed must be output as EBCDIC characters.

The standard input process for binary data is a two–step one, in which the character
data are first packed to form decimal data and then converted to binary.

The standard process to output binary data from a register is also a two–step one.
First convert the binary to decimal data and then use unpack or the edit instruction
to produce the printable EBCDIC characters.

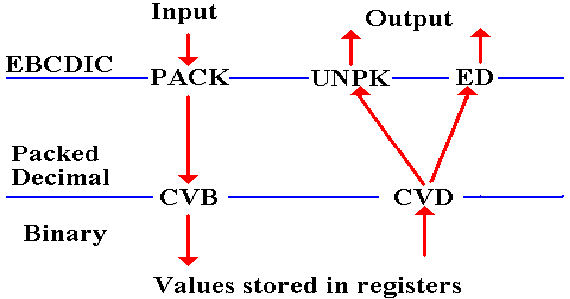
Conversion Between Packed Decimal and Binary

These two conversion instructions are each a type RX instruction.

CVB (Convert to Binary) converts packed decimal data from storage into
binary form in a general–purpose register.

CVD (Convert to Decimal) converts binary data in a general–purpose register
into packed decimal form in storage.

The format of each is OP R1,D2(X2,B2).

Template for the instructions: CVB Register,Storage_Location

CVD Register,Storage_Location

For the CVB instruction, the Storage Location contains the packed decimal value that
is to be converted to binary and placed in the register.

For the CVD instruction, the Storage Location that will receive the packed decimal value
that is the result of converting the value in the register.

It is standard practice to use the floating point data type D (double word) to
declare the storage location.

Why A Floating Point Type Here?

The D data type declares a double precision floating point value, which occupies
eight bytes (64 bits) and is automatically aligned on a double–word boundary.

In other words, its address is a multiple of 8.

The true requirement for the operand is that it be exactly eight bytes long
and begin on a double–word boundary. The D declaration fills the bill.

Consider the following code, which is rather standard.

CVB R6,D1

D1 DS D DOUBLE WORD OR 8 BYTES

One might also write the following, if one is careful.

CVB R6,D2

D2 DS PL8 EIGHT BYTES FOR UP TO 15 DIGITS

The difficulty here is insuring that D2 is properly aligned on a double–word boundary.
While this can be done, it is less error–prone to use the D type and have the assembler
automatically do the alignment for you.

Example and Comments

How many digits do I really need?

The biggest value storable as a 32–bit binary number is 2147483647.

This number has 10 digits, which will be converted to 11 digits for storage in
Packed Decimal format. A 4–byte full–word will store only seven digits.

There is no data size that automatically takes 6 bytes and no provision for aligning
an address on a multiple of six. The obvious choice is storage as a double–word.

Input example

ZAP D1,AMTPACK TRANSFER TO THE DOUBLE WORD

CVB R5,D1 CONVERT TO BINARY

D1 DS D THIS RESERVES EIGHT BYTES

Output example

CVD R5,D2 PLACE INTO A DOUBLE WORD

ZAP AMTPACK,D2 TRANSFER TO THE PACKED WORD

D2 DS D THIS ALSO RESERVES EIGHT BYTES

Loading Values: L, LH, and LR

The general–purpose registers are designed to store and manipulate binary data
that are stored in the form of 32–bit two’s–complement integers.

As an aside, remember two facts about such numbers.

1. The IBM standard is to number the bits from left to right as 0 through 31.
The sign bit is called “Bit 0” and the units bit on the right “Bit 31”.

2. IBM will often call this “31 bit data”, as the value has a 31–bit magnitude
(stored in bits 1 – 31) and a sign bit.

We first discuss three of the standard instructions used to load values into a register.

L Load a full–word value into the register.

LH Load a half–word value into the register.
The 16–bit value is sign extended into 32–bits for the register.

LR Copy a value from one register to another register.

Note: None of these instructions will set a condition code.

Do not load a register and expect a condition code to reflect the value loaded.

L (Load 32–bit Full–word)

The instruction is a type RX, with format L R1,D2(X2,B2).

Here is a template for the instruction: L Reg,Full_Word

The first operand specifies any general–purpose register.

The second operand references a full–word in storage, usually aligned on a full–word
boundary. If the second operand is a literal, the assembler will align it properly.

Here are some examples of common usage. Other examples will be discussed later.

L R2,=F‘4000’ R2 GETS DECIMAL 4000

L R3,F1 R3 ALSO GETS DECIMAL 4000

L R4,H1 THIS IS PROBABLY A MISTAKE.

F1 DC F‘4000’

H1 DC H‘2000’

H2 DC H‘3000’

Note again, it is usually a mistake to attempt to use a full–word load to place a
half–word value into a register.

LH (Load 16–bit Half–word)

The instruction is a type RX, with format LH R1,D2(X2,B2).

Here is a template for the instruction: LH Reg,Half_Word

The first operand specifies any general–purpose register.

The second operand references a half–word in storage, usually aligned on a half–word
boundary. If the second operand is a literal, the assembler will align it properly.

The assembler loads the half–word into the rightmost 16 bits of the register (16 – 31)
and then propagates the half–word’s sign bit through the left 16 bits of the register.

Here are some examples of common usage. Other examples will be discussed later.

LH R2,=H‘4000’ R2 GETS DECIMAL 4000

LH R3,H1 R3 GETS DECIMAL 2000

LH R4,F1 THIS IS PROBABLY A MISTAKE.

F1 DC F‘4000’

H1 DC H‘2000’

Sign Extension for LH

Consider two 16–bit integers that are stored as half–words in two’s–complement form.

The positive number + 100 is stored as 0000 0000 0110 0100, or X‘0064’.

The negative number –100 is stored as 1111 1111 1001 1100 or X‘FF9C’

Consider the code fragment below.

LH R7,=H‘100’

After this, register R7 contains the full–word value +100, as shown below.

Left half–word				Right half–word
0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
0000	0000	0000	0000	0000	0000	0110	0100

Now consider the code fragment.

LH R8,=H‘-100’

After this, register R8 contains the full–word value –100, as shown below.

Left half–word				Right half–word
0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
1111	1111	1111	1111	1111	1111	1001	1100

LR (Load Register)

The instruction is a type RR, with format LR R1,R2.

Each operand specifies any general–purpose register.

The contents of the register specified as the second operand are
copied into the register specified as the first operand.

Consider the code fragment below.

L R9,=H‘200’ REGISTER 9 GETS DECIMAL 200

LR R7,R9 REGISTER 7 ALSO GETS 200

LM (Load Multiple Registers)

The LM instruction loads data from main storage into more than one register.

The instruction is a type RS with format LM R1,R3,D2(B2).

Operand 1 represents the first register in a range of registers.

Operand 2 represents the second register in the range of registers.

Operand 3 represents a full–word in memory, the first of a range of adjacent
full–word values, one for each register in the range R1,R3.

The register numbers “wrap around”, so that 15,1 specifies the three registers 15, 0, 1.

Example code:

LM R6,R8,F1 LOAD R6, R7, R8 FROM F1, F2, F3

LM R15,R2,F1 LOAD R15, R0, R1, R2 FROM F1 TO F4

F1 DC F‘1111’

F2 DC F‘2222’

F3 DC F‘3333’

F4 DC F‘4444’

LM and the Standard Closing Code

Look again at part of the standard closing code for our programs.

******************* END LOGIC **************************

L R13,SAVEAREA+4 POINT AT OLD SAVE AREA

LM R14,R12,12(R13) RESTORE THE REGISTERS

LA R15,0 RETURN CODE = 0

BR R14 RETURN TO OPERATING SYSTEM

**************************************************************

The label SAVEAREA references a sequence of full words used to save information
used when returning to the operating system.

The second full–word in this area, at address SAVEAREA+4, holds the address of
the block of memory used to save the register information.

More specifically, the old register values are saved in a block beginning with the
fourth full–word (at offset 12) in the block with address now in R13.

The instruction LM R14,R12,12(R13) loads the 15 registers R14 through R12,
omitting only R13, with the 15 full–word values beginning at the specified address.

The instruction LA R15,0 is a use of a Load Address instruction that we shall discuss
very shortly. I would prefer something like LH R15,=H‘0’, which is equivalent.

Loading Addresses

Up to now, we have discussed “value loaders”, such as the following example.

L R3,FW1

This finds the full–word at address FW1 and loads its value into register R3.

At times, we shall need not the value stored at an address but the address itself.
One possibility would be to store a return address to be used by a subroutine.

There are two common ways to access the address and store it into a register.

1. Use the L (Load full–word) instruction and use an address literal

2. Use the LA (Load Address) instruction and use the label.

The following two statements are equivalent. Each loads R1 with the address FW1.

L R1,=A(FW1)

LA R1,FW1

In the System/360 and System/370 the address is treated as a 24–bit unsigned integer,
which can be represented by six hexadecimal digits.

If the address of FW1 is X‘112233’, register R1 gets X‘00112233’.

LA (Load Address)

The instruction is a type RX, with format LA R1,D2(X2,B2).

Here is a template for the instruction: LA Reg,Address

The first operand specifies any general–purpose register.

The second operand references a storage address in the form D2(X2,B2).

Consider the following fragment of code, which indicates one use of the instruction.

LA R9,A10

A10 DC F‘100’

Suppose that label A10 is subject to base register 3 containing value X‘9800’
with a displacement of X‘260’. The object code for the LA instruction is as follows.

41 90 32 60

The code for the LA instruction is X‘41’. The second byte “90” is of the form R1X2,
where R1 is the target register and X2 is the unused index register.

The LA instruction causes register R9 to be get value X‘9800’ + X‘260’ = X‘9A60’.

LA: A Second Look

The instruction is a type RX, with format LA R1,D2(X2,B2).

Consider the example above, coded as LA R9,X‘260’(0,3).

Again, the object code for this is 41 90 32 60.

Let’s analyze this object code. What it says is the following:

1) Take the contents of register 3 X‘9800’

2) Add the value of the offset X‘260’

3) Add the contents of the index X‘000’
(here no index register is used)

4) Get the value X‘9A60’

5) Place that value into register R9

But note: While we call this an address, it is really just an unsigned binary number.

This gives rise to a common use of the LA instruction to load a constant
value into a general–purpose register.

LA: Load Register with Explicit Value

Consider the instruction LA R8,4(0,0).

The object code for this is 41 80 00 04.

The code is executed assuming no base register and no index register.
The number 4 is computed and loaded into register 8.

The following instruction is considered identical: LA R8,4.

Note that the second operand in this form of the instruction is a non–negative
integer that is treated by the assembler as a displacement.

This implies that the value must be representable as a 12–bit unsigned integer,
specifically that it must be a non–negative integer not larger than 4,095 (decimal).

Consider now the line from the standard ending code of our programs.

LA R15,0 RETURN CODE = 0

This places the value 0 into the destination register.

Instructions: Surface Meaning and Uses

In the previous example, we see a trick that is commonly used by assembly
language programmers: find what the instruction really does and exploit it.

The surface meaning of the LA instruction is simple: load the address of a
label or symbolic address into a given register.

The usage to load a register with a small non–negative constant value is an
immediate and logical result of the way the object code is executed.

The two goals of such tricks seem to be:

1) To gain coding efficiency, and

2) To show the ingenuity and cleverness of the programmer.

Consider the following two groupings, which seem to do the same thing.

LA R8,26 TYPE RX INSTRUCTION, 4 BYTES LONG

LH R8,H26 TYPE RX INSTRUCTION, 4 BYTES LONG

H26 DC H‘26’ CONSTANT TAKES 2 BYTES

The second combination requires 6 bytes to the 4 required for the first one.
If memory is tight, this might be a valuable saving.

Storing Register Values: ST, STH, and STM

ST (Store Full Word) is a type RX instruction, with format ST R1,D2(X2,B2).

STH (Store Half Word) is a type RX instruction, with format STH R1,D2(X2,B2).

STM (Store Multiple) is a type RS instruction, with format STM R1,R3,D2(B2).

The ST instruction stores the full–word contents of the register, specified in the
first operand, into the full word at the address specified by the second operand.

The STH instruction stores the rightmost 16 bits of the register specified by the
first operand into the half word at the address specified by the second operand.

For STM (Store Multiple Registers), the first two operands specify a range of
registers to be stored. Remember that the register numbers “wrap around”

STM R7,R10,X2 STORE THE FOUR REGISTERS R7,R8,R9,AND R10
INTO FOUR FULL-WORDS BEGINNING AT X2

STM R10,R7,X4 STORE THE 14 REGISTERS R10 THROUGH R7
(ALL BUT R8 AND R9) INTO 14 FULL-WORDS

Standard Boilerplate Code

Once again, we examine some of the standard code used in all of our programs.

The standard startup code includes the following fragment.

SAVE (14,12) SAVE THE CALLER'S REGISTERS

This macro generates the following code.

STM 14,12,12(13) STORE REGISTERS 14 THROUGH 12

(15 IN ALL) INTO THE ADDRESS
12 OFFSET FROM BASE REGISTER 13.

We might have concluded our code with the macro

RETURN (14,12)

This expands into the code we actually use in our programs.

LM 14,12,12(13)

LA R15,0 RETURN CODE = 0

BR R14 RETURN TO OPERATING SYSTEM

Binary Arithmetic: Addition and Subtraction

There are six instructions for addition and subtraction.

Mnemonic Description Type Format

A Add full–word to register RX A R1,D2(X2,B2)

S Subtract full–word from register RX S R1,D2(X2,B2)

AH Add half–word to register RX AH R1,D2(X2,B2)

SH Subtract half–word from register RX SH R1,D2(X2,B2)

AR Add register to register RR AR R1,R2

SR Subtract register from register RR SR R1,R2

In each of these, the first operand is a register. It is this register that has its
value changed by the addition or subtraction.

For the half–word instructions (AH and SH), the second operand references a
half–word storage location. The 16–bit contents of this location are sign extended
to a full 32–bit word before the arithmetic is performed.

Binary Arithmetic: Half–word arithmetic

Examples of the instructions

L R7,FW1 LOAD REGISTER FROM FW1

A R7,FW2 ADD FW2 TO REGISTER 7

S R7,=F‘2’ SUBTRACT 2 FROM R7

AR R7,R8 ADD CONTENTS OF R8 TO R7

SR R7,R9 SUBTRACT R9 FROM R7

SR R8,R8 SET R8 TO ZERO

FW1 DC F‘2’ JUST A FEW VALUES FOR

FW2 DC F‘4’ FW1 AND FW2.

As noted indirectly above, one has two options for operating on one register.

AR R7,R7 DOUBLE THE CONTENTS OF R7
(MULTIPLY R7 BY 2)

SR R9,R9 SET R9 TO ZERO.

Comparing Binary Data: C, CH, and CR

There are three instructions for binary comparison with the value in a register.

Mnemonic Description Type Format

C Compare full–word RX C R1,D2(X2,B2)

CH Compare half–word RX CH R1,D2(X2,B2)

CR Compare register to register RX AH R1,D2(X2,B2)

Each comparison sets the expected condition code.

Condition Condition Code Branch Taken

Operand 1 = Operand 2 0 (Equal/Zero) BE, BZ

Operand 1 < Operand 2 1 (Low/Minus) BL, BM

Operand 1 > Operand 2 2 (High/Plus) BH, BP

Don’t forget that literal arguments can be used with either C or CH, as in this example.

C R9,=F‘0’ COMPARE THE REGISTER TO ZERO

BH ISPOS IT IS POSITIVE

BL ISNEG NO, IT IS NEGATIVE.

An Extended Example

This example takes the value in HW1, makes it non–negative, and then sums
backwards N + (N – 1) + … + 2 + 1 + 0.

SR R6,R6 SET R6 TO ZERO

LH R5,HW1 GET THE VALUE INTO R5

SR R6,R5 SUBTRACT TO SET THE CONDITION CODE

C R6,=F‘0’ IS R6 POSITIVE? (IF SO R5 IS NEGATIVE)

BH POS YES R6 IS POSITIVE.

LR R6,R5 R5 IS NOT NEGATIVE. COPY R5 INTO R6

* NOW R6 CONTAINS THE ABSOLUTE VALUE OF THE HALF-WORD

POS SR R5,R5 R5 WILL HOLD THE TOTAL. SET TO ZERO.

LOOP AR R5,R6 ADD R6 TO R5

S R6,=F‘1’ DECREMENT R5 BY 1

C R6,=F‘0’ IS THE VALUE STILL POSITIVE?

BH LOOP YES, GO BACK AND ADD AGAIN.

* THE SUM IS FOUND IN R5.

Register Shift Operations

We now discuss a number of shift operations performed on registers.

Mnemonic Description Type Format

SLA Shift left algebraic RS SLA R1,D2(B2)

SRA Shift right algebraic RS SRA R1,D2(B2)

SLL Shift left logical RS SLL R1,D2(B2)

SRL Shift right logical RS SRL R1,D2(B2)

SLDA Shift left double algebraic RS SLDA R1,D2(B2)

SRDA Shift left double algebraic RS SRDA R1,D2(B2)

SLDL Shift left double logical RS SLDL R1,D2(B2)

SRDL Shift right double logical RS SRDL R1,D2(B2)

The algebraic shifts preserve the sign bit in a register, and thus are useful for arithmetic.

The logical shifts do not preserve the sign bit.

The shift operations set the standard condition codes, for use by BC and BCR.

The register numbers for the double shift instructions must be an even number,
referencing the first of an even–odd register pair (see below).

Shift Instructions: Object Code Format

All shift instructions are four–byte instructions of the form OP R1,R3,D2(B2).

Type	Bytes		1	2	3	4
RS	4	R1,R3,D2(B2)	OP	R1 R3	B2 D2	D2D2

The first byte contains the 8–bit instruction code.

The second byte contains two 4–bit fields, each of which encodes a register number.
The first register number (R₁) is the register to be shifted. The second register number
(R₃) is not used and conventionally set to 0.

The third and fourth byte contain a 4–bit register number and 12–bit value. In many
type RS instructions, these would indicate a base register and a displacement to be
used to specify the memory address for the operand in storage.

For the shift instructions, this field is considered as a value to indicate the shift count.
The value is in the form below. B is the number of the register to be used as a base
for the value. The next three hexadecimal digits are added to the value in that register.

The sum is used as a shift count, not as an address. Often the base register is 0,
indicating that no base register is used.

B D1

D2 D3

Example Object Code Analysis: SLL

Shift Left Logical Operation code = X‘89’

This is also a type RS instruction, though the appearance of a typical use seems to deny
this. Consider the following instruction which shifts R6 left by 12 bits.

SLL R6, 12 Again, I assume we have set R6 EQU 6

The above would be assembled as 89 60 00 0C Decimal 12 is X‘C’

The deceptive part concerns the value 12, used for the shift count. Where is that stored?

The answer is that it is not stored, but is used as a value for the shift count.

The object code 00 0C literally indicates the computation of a value that is an sum of
decimal 12 from the value in base register 0. But “0” indicates that no base register is
used, hence the value for the shift is decimal 12.

Here are three lines from a working program I wrote on 2/23/2009.

000014 5840 C302 00308 47 L R4,=F'1'

000018 8940 0001 00001 48 SLL R4,1

00001C 8940 0002 00002 49 SLL R4,2

Single Shifts: Algebraic and Logical

Here are some diagrams describing shifts in a single register. These examples will
assume an 8–bit register with the IBM bit numbering scheme; 32 bits are hard to draw.

This figure illustrates logical shifts by 1 for these imaginary 8–bit registers.

This figure illustrates algebraic shifts by 1 for these imaginary 8–bit registers.

The actual IBM assembler shift instructions operate on 32–bit registers and can shift by
any number of bit positions. For single register shifts, the shift count should be a
non–negative integer less than 32. For double register shifts, the upper limit is 63.

Double Register Shifts

Each of these four instructions operates on an even–odd register pair.

The algebraic shifts preserve the sign bit of the even register; the logical shifts do not.

Here is a diagram illustrating a double algebraic right shift.

If the above example were a logical double right shift, a 0 would have been
inserted into the leftmost bit of the even register.

Remember to consider the shifts in register pairs, preferably even–odd pairs.

Consider the following code: SR R9,R9 This clears R9

SRDL R8,32

The double–register right shift moves the contents of R8 into R9 and clears R8,
as it is a logical shift.

Single Register Left Shifts: Another View

First consider the left shifts. There are two single–register variants: SLL and SLA.

For an N–bit logical left shift, bits 0 through (N – 1) are shifted out of the register
and discarded. Bits 31 through (32 – N) are filled with 0.

Bit 0 is not considered as a sign bit in a logical shift; it may change values.

For an N–bit arithmetic left shift, bits 1 through N are shifted out of the register
and discarded. Bits 31 through (32 – N) are filled with 0. Bit 0 (the sign bit)
is not changed.

The overflow bit can be set by an arithmetic left shift. This will occur if
the bit shifted out does not match the sign bit that is retained in bit 0.

We shall see later that setting the overflow bit indicates that the result of the
shift cannot be viewed as a valid result of an arithmetic operation.

Single Register Right Shifts: Another View

Now consider the left shifts. There are two single–register variants: SRL and SRA.

For either of these shift types, a shift by N bit will cause the N least significant bits
to be shifted out of the register and discarded.

For an N–bit logical right shift, the value 0 is shifted into the N most significant bits,
bits 0 through (N – 1) of the register. Bit 0 is not considered a sign bit and is
shifted into bit N of the register. The sign of the number may change.

For an N–bit arithmetic right shift, bit 0 is considered as a sign bit. Bit 0 is not changed,
but is shifted into bits 1 through N of the register. At the end, the (N + 1) most
significant bits of the register contain what used to be bit 0 (the sign bit).

For an arithmetic right shift, the sign of the shifted result is the same as that of the
original. If the sign bit originally is 0, the SRL and SRA produce identical results.

Double Register Shifts: Another View

The double register shifts are just generalizations of the single register shifts.

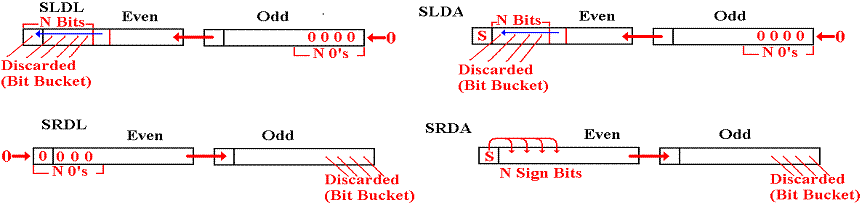
In these double register shifts, a pair of registers is viewed as a single 64–bit value.

The IBM coding convention (and possibly the CPU hardware) calls for this pair to be
what is called an even–odd pair, in which the odd number is one more than the even.

Examples of even–odd register pairs are: 4 and 5, 6 and 7, 8 and 9, 10 and 11.

Consider the two registers R5 and R6. While it is true that 5 is an odd number
and 6 is an even number; these two registers do not form an even–odd pair.

Each of these is a member of a distinct even–odd pair.

Shift Examples

Here are some typical shift examples, with comments.

SRA R9,2 Algebraic right shift by 2 bit positions, equivalent to division
by 4. SRA by N bit positions is equivalent to division by 2^N.

SLA R8,3 Algebraic left shift by 3 bit positions, equivalent to multiplication
by 8. SLA by N bit positions is equivalent to multiply by 2^N.

NOTE: Multiplication using the M, MH, or MR instructions is rather slow, as is
division with either D or DR. It is almost universal practice to use arithmetic
left shifts to replace multiplication by a power of 2 and arithmetic right
shifts to replace division by a power of 2.

Example: Consider the following three lines of code.

L R5,AVAL ASSUME AVAL IS THE LABEL FOR A FULL-WORD

LR R6,R5 COPY VALUE INTO R6

SRA R6,3 SAME AS MULTIPLY BY 8

AR R6,R5 R6 NOW HAS 9 TIMES THE VALUE IN R5.

More on Shifting and Arithmetic

The association of arithmetic left shifting with multiplication, and arithmetic right
shifting with division is useful. However, there are limits to this interpretation.

To illustrate this for multiplication, I select an integer that is a simple power of 2,
4096 = 2¹². As a 16–bit integer, this would be stored in memory as follows.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0

Taking the two’s–complement of the above, we find that –4096 is stored as follows.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0

We shall use each of these two integer values to illustrate the limits of the arithmetic
left shift. We shall then consider the following pair as subject to an arithmetic right shift.

+32 = 2⁵ is stored as follows.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0

–32 is stored as follows.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0

Arithmetic Left Shifts as Multiplication

We first consider some left shifts that can validly be interpreted as multiplication.
For each of these integers, consider a SLA 2 (Arithmetic Left Shift by 2 bit positions).

According to our interpretation, a SLA 2 should be equivalent to multiplication by 2² = 4.

The 4096 = 2¹² becomes 16384 = 2¹⁴. This is as it should be.

4096·4 = 16384 and 2¹²·2² = 2¹⁴.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0

The –4096 = –(2¹²) becomes –16384 = –(2¹⁴). This is as it should be.

(–4096)·4 = –16384 and –(2¹²)·2² = –(2¹⁴).

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Overflow on Shifting Left (Multiplication)

Consider again 4096 = 2¹², stored as a 16–bit integer.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0

Consider the result of SLA 3 (Arithmetic Left Shift by 3 bit positions).

According to our interpretation, a SLA 3 should be equivalent to multiplication by 2³ = 8.
4096·8 = 32768 and 2¹²·2³ = 2¹⁵ = 32768.

But, the 4096 = 2¹² becomes –32768 = –(2¹⁵). The sign has “gone bad”, as a result of
arithmetic overflow.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

But consider the same operation on –4096 = –(2¹²).

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0

After the shift, we have the proper result; –4096·8 = –32768.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

More on Overflow While Shifting Left

In this illustration we continue to focus on 16–bit two’s complement integers.
A 32–bit representation would show the same problem, only at larger values.

Suppose we have the valid integer –32,768 = –(2¹⁵). This is stored as follows.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

Suppose we attempt a SLA (Shift Left Arithmetic) by any positive bit count.
The result will remain the same. The sign bit is always preserved in an arithmetic shift.

In attempting a SLA as a substitute for multiplication by a power of two, we find that.

(–32,768)·2 = –32,768.

(–32,768)·4 = –32,768.

(–32,768)·8 = –32,768.

In other words, once overflow has been hit, SLA ceases to serve as multiplication.

Arithmetic Right Sifting as Division

Here the results are a bit less strange. First consider our positive number, +32.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0

A SRA 4 (Arithmetic Right Shift by 4) should yield 32/16 = 2. It does.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0

Further shifting this result by 1 bit position will give the value 1 (as expected).

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1

However, any more SRA (Arithmetic Right Shifts) will give the value 0.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

This is as expected for integer division, and is not surprising.

More on Arithmetic Right Sifting as Division

Here the results are a bit less strange. Now consider our negative number, –32.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0

A SRA 3 (Arithmetic Right Shift by 3) should yield (–32)/8 = (–4). It does.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0

A SRA 2 (Arithmetic Right Shift by 2) should yield (–4)/4 = (–1). It does.

Sign	2^14	2^13	2^12	2^11	2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

But note that further Arithmetic Right Shifts continue to produce the result –1.

What we are saying is that (–1) / 2 = –1.

If the above is acceptable, then the SRA works well as a substitution for
division by a power of two.

Register Pairs: Multiplication and Division

We now discuss two instructions that, in their full–word variants, demand the
use of a 64–bit “double word”. Rather than use the type, we use a pair of registers.

The assembly language definition calls for “even–odd register pairs”.

Each pair of registers is referenced by its (lower numbered) even register.

Standard pairs from the general–purpose registers that are not reserved for other use:

R4 and R5 R8 and R9

R6 and R7 R10 and R11

When such a pair is referenced by a multiply or divide instruction, it is treated as
a 64–bit two’s–complement integer with the sign in bit 0 of the even register.

Remember that the bits of a register are numbered left to right, so that bit 0 is
the sign bit and bit 31 is the rightmost (least significant) bit.

Examples: M R4,F2 MULTIPLY VALUE IN R5 BY VALUE IN
FULL-WORD F2. RESULTS IN (R4, R5)

D R6,F3 DIVIDE 64-BIT NUMBER IN (R6, R7) BY F3

Full–Word Multiplication

This slide will cover the two multiplication instructions based on full words.
The half–word multiplication instruction will be discussed later.

The two instructions of interest here are:

Mnemonic Description Type Format

M Multiply full–word RX M R1,D2(X2,B2)

MR Multiply register RR MR R1,R2

For each of these, one uses a selected even–odd pair to hold the 64–bit product.
Here is the status of the registers in the selected pair; think (4, 5) or (8, 9), etc.

	Even Register	Odd Register
Before multiplication	Not used: contents are ignored	Multiplicand
After multiplication	Product: high–order 32 bits	Product: low–order 32 bits

If the product can be represented as a 32–bit number, the even register will contain
the extended sign bit, so that the 64–bit number in the register pair has the right sign.

Note that the multiplication overwrites the value of the multiplicand in the odd register.

Full–Word Multiplication: Examples

One code fragment, in which I first clear R4 for no purpose whatsoever.
In the first fragment, the starting value in R4 is irrelevant, as it is ignored.

Each example assumes two full–words: MULTCAND and MULTPLER.

L R5,MULTCAND LOAD THE MULTIPLICAND INTO R5.

SR R4,R4 CLEAR R4. THIS IS REALY USELESS.

M R4,MULTPLER MULTIPLY BY A FULLWORD

* R4 NOW HAS BITS 0 – 31 OF THE 64-BIT PRODUCT

* R5 NOW HAS BITS 32 – 63 OF THE 64-BIT PRODUCT

Another code fragment:

L R9,MULTCAND LOAD THE MULTIPLICAND INTO R9.

L R5,MULTPLER LOAD MULTIPLIER INTO R5

MR R8,R5 MULTIPLY BY FULL-WORD VALUE IN R5

* R8 NOW HAS BITS 0 – 31 OF THE 64-BIT PRODUCT

* R9 NOW HAS BITS 32 – 63 OF THE 64-BIT PRODUCT

Half–Word Multiplication

Mnemonic Description Type Format

MH Multiply half–word RX MH R1,D2(X2,B2)

This instruction requires only one register. It is loaded with the multiplicand before the
multiplication, and receives the product.

Note that this is the product of a 32–bit number (in the register) and a 16–bit number
in the half–word in memory. This will result in a 48–bit product.

Of bits 0 – 47 of the product, only bits 16 – 47 are retained and kept in the 32–bit
register as the product. If the absolute value of the product is greater than 2³¹, the sign
bit of the result (as found in the register) might not be the actual sign of the product.

Here is an example of a proper use of the instruction, which will give correct results.

LH R3,MULTCAND Each of these two arguments is a half–word

MH R3,MULTPLER with value in the range: –2¹⁵ £ N £ (2¹⁵ – 1).

MULTCAND DC H‘222’

MULTPLER DC H‘44’

The magnitude of the product will not exceed (2¹⁵)·(2¹⁵) = 2³⁰, an easy fit for a register.

Full–Word Division

This slide will cover the two division instructions based on full words.
The half–word division instruction will be discussed later.

The two instructions of interest here are:

Mnemonic Description Type Format

D Divide full–word RX D R1,D2(X2,B2)

DR Divide register RR DR R1,R2

For each of these, one uses a selected even–odd pair to hold the 64–bit dividend.

Here is the status of the registers in the selected pair; think (4, 5) or (8, 9), etc.

	Even Register	Odd Register
Before division	Dividend: high–order 32 bits	Dividend: low–order 32 bits
After division	Remainder from division	Quotient from division

In each of the full–word division operations, it is important to initialize the even register
of the pair correctly. There are two cases to consider.

1. The dividend is a full 64–bit number, possibly loaded with a LM instruction.

2. The dividend is a 32–bit number. In that case, we need to initialize both registers.

Full–Word Division: Example 1

In this example, I am assuming a full 64–bit dividend that is stored in two adjacent
full words in memory. I use this memory structure to avoid adding anything new.

LM R10,R11, DIVHI LOAD TWO FULLWORDS

D R10,DIVSR NOW DIVIDE

* R10 CONTAINS THE REMAINDER

* R11 CONTAINS THE QUOTIENT

DIVHI DC F‘1111’ ARBITRARY NUMBER THAT IS NOT TOO BIG

DIVLO DC F‘0003’ ANOTHER ARBITRARY NUMBER

DIVSR DC F‘19’ THE DIVISOR

Important Note: This process of assembling a 64–bit dividend from two full words
might run into problems if DIVLO is seen as negative.

Here, I choose to ignore that point.

Full–Word Division: Example 2

In this example, I am assuming a 32–bit dividend and using a more standard
approach. Please note that it works only for positive dividends.

SR R10,R10 SET R10 TO 0

L R11,DIVIDEND LOAD FULL–WORD DIVIDEND

D R10,DIVISOR DO THE DIVIDING

* R10 CONTAINS THE REMAINDER

* R11 CONTAINS THE QUOTIENT

DIVIDEND DC F‘812303 JUST SOME NUMBER.

DIVISOR DC F‘16384’ A POWER OF TWO, SEE NOTE BELOW

NOTES: 1. This works only for a positive dividend. The reason is that, by clearing
the even register of the even–odd pair, I have declared the 64–bit dividend
to be a positive number, even if R11 is loaded with a negative number.

2. There is a much faster way to divide any number by a power of two.
This method, using a shift instruction, will be discussed later.

Full–Word Division: Example 3

In this example, I am assuming a 32–bit dividend and using the standard approach
that will work correctly for all dividends. The dividend is first loaded into the even
register of the even–odd pair and then shifted into the odd register.

This shifting causes the sign bit of the 64–bit dividend to be set correctly.

L R10,DIVIDEND LOAD INTO THE EVEN REGISTER

SRDA R10,32 SHIFTING BY 32 BITS PLACES

* THE DIVIDEND INTO R11.

* R10 RETAINS THE SIGN BIT

D R10,DIVISOR DO THE DIVIDING

* R10 CONTAINS THE REMAINDER

* R11 CONTAINS THE QUOTIENT

DIVIDEND DC F‘812303 JUST SOME NUMBER.

DIVISOR DC F‘16384’ A POWER OF TWO, SEE NOTE BELOW

We shall discuss this a bit more after we have discussed the shift operations.

Full–Word Division: Example 4

Here is a more realistic example of the use of a full 64–bit dividend.

Code fragment 1: Create the 64–bit product and store in adjacent full words.

L R5,MCAND LOAD THE MULTIPLICAND INTO R5.

M R4,MPLER MULTIPLY BY A FULLWORD

* R4 NOW HAS BITS 0 – 31 OF THE 64-BIT PRODUCT

* R5 NOW HAS BITS 32 – 63 OF THE 64-BIT PRODUCT

STM R4,R5,PRODHI STORE THE 64-BIT PRODUCT

Code fragment 2: Some time later use the 64–bit product as a dividend for division.

LM R10,R11,PRODHI LOAD TWO FULLWORDS

D R10,DIVSR NOW DIVIDE

* R10 CONTAINS THE REMAINDER

* R11 CONTAINS THE QUOTIENT

PRODHI DC F‘0’ TWO FULL WORDS SET ASIDE

PRODLO DC F‘0’ 64 BITS (8 BYTES) OF STORAGE.

Diversion: Shifting the Dividend Into Place

Consider two possible dividends: + 100 and – 100.

Consider the code fragment below.

LH R6,=H‘100’

SRDA R6,32

After the first instruction is executed, register R6 contains the full–word value +100,
as shown below.

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
0000	0000	0000	0000	0000	0000	0110	0100

After the shift in the second instruction, the contents of R6 have been shifted to R7,
leaving only the sign bit in R6.

R6

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
0000	0000	0000	0000	0000	0000	0000	0000

R7

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
0000	0000	0000	0000	0000	0000	0110	0100

Shifting the Dividend Into Place (Part 2)

Now consider the code fragment.

LH R8,=H‘-100’

SRDA R8,32

After the first instruction is executed, register R8 contains the full–word value –100,
as shown below.

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
1111	1111	1111	1111	1111	1111	1001	1100

After the shift in the second instruction, the contents of R8 have been shifted to R9,
leaving only the sign bit in R8.

R8

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
1111	1111	1111	1111	1111	1111	1111	1111

R9

0 – 3	4 – 7	8 – 11	12 – 15	16 – 19	20 – 23	24 – 27	28 – 31
1111	1111	1111	1111	1111	1111	1001	1100