Declaring
Floating Point Data
There are three ways to declare floating–point
storage. These are
E Single–precision floating point,
D Double–precision floating point, and
L Extended–precision
floating point.
The
lengths of these data types are as follows:
E 32 bits or 4 bytes.
D 64 bits or 8 bytes.
L 128 bits or 16 bytes.
We shall focus on the first two data types (E and
D). These evolved from the
48–bit floating point data type used on the IBM 7094, a predecessor of the
IBM 360.
The creation of two related data types was a
compromise necessary to
drop the 48–bit data type.
Details of
the Format
The floating–point number consists of a sign,
characteristic (exponent), and
a fraction. The bit allocations
for each of the three formats is shown below.
|
Format |
Length |
Sign bit |
Characteristic |
Fraction |
|
E |
4 bytes |
0 |
1 – 7 |
8 – 31 |
|
D |
8 bytes |
0 |
1 – 7 |
8 – 63 |
|
L |
16 bytes |
0 |
1 – 7 |
8 – 127 |
Recall
that IBM numbers bits from left to right.
The sign bit, in bit position 0, applies to the
fraction. The two values are:
0 the number is not a negative number;
it is either positive or
zero.
1 the number is a negative number.
Byte 0
(the most significant byte) or each representation holds both
the sign for the fraction, and
the characteristic field, which holds the exponent.
Details of
the Exponent Field
Bits 1 – 7 of each format hold the characteristic
field, which is defined to be
the exponent in excess–64 notation; it is (exponent + 64).
As a seven–bit unsigned integer can store values in
the range 0 through 127,
we have 0 £ (exponent + 64) £ 127, or
–64 £ exponent £ 63.
The leftmost byte of the format stores both the sign
and exponent.
|
Bits |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Field |
Sign |
Exponent in Excess–64 format |
||||||
Examples
Positive
number, Exponent = –8 E + 64 =
56 = 48 + 8 = X’38’ = B’011 1000’.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Sign |
3 |
8 |
|||||
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
The
value stored in the leftmost byte is 0011 1000 or 38.
Normalized
Formats
All floating point formats are of the form (S, E, F)
representing (–1)S·BE·F
S the sign bit, 1 for negative and 0
for non–negative.
B the base of the
number system; one of 2, 10, or 16.
E the exponent.
F the fraction.
The IBM 370 format uses base 16.
Each of the formats represents the numbers in
normalized form.
For IBM 370 format, this implies that 0.0625 < F £ 1.0. Note
(1/16) = 0.0625.
In byte addressing, the layout of the E and D formats
is as follows.
|
Byte |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
E |
Sign & |
Fraction |
|
|||||
|
D |
Sign & |
Fraction |
||||||
Converting
Decimal to Hexadecimal
The first step in producing the IBM 370 floating point
representation
of a real number is to convert that number into hexadecimal format.
The process for conversion has two steps,
one each for the integer and
fractional part.
Example: Represent
123.90625 to hexadecimal.
Conversion of the integer part is achieved by repeated
division with remainders.
123 / 16 = 7 with
remainder 11 X’B’
7 / 16 = 0 with
remainder 7 X’7’.
Read bottom to top as X’7B’. Indeed 123 = 7·16 + 11 = 112 + 11.
Conversion of the fractional part is achieved by
repeated multiplication.
0.90625 · 16 = 14.5 Remove the 14 (hexadecimal E)
0.5 · 16 = 8.0 Remove the 8.
The answer is read top to bottom as E8.
The answer is that 123.90625 in decimal is represented by X’7B.E8’.
Converting Decimal
to IBM 370 Floating Point Format
The decimal number is 123.90625.
Its hexadecimal representation is 7B.E8.
Normalize this by moving the decimal point two places
to the left.
The number is now 162 · 0.7BE8.
The sign is 0, as the number is not negative.
The exponent is 2, E + 64 = 66 = X’42’. The leftmost byte is X’42’.
The fraction is 7BE8.
The left part of the floating point data is 427BE8.
In single precision, this would be represented in four
bytes as 42 78 E8 00.
Floating–Point
Registers
In addition to the 16 general–purpose registers, the
IBM System/370 supports four
floating–point registers. Later models
support more.
Each floating–point register is a 64 bit register,
suitable to hold the D data type.
These registers are numbered 0, 2, 4, and 6.
The even numbering was probably intended to reinforce
the idea that each of
these registers has twice the length of a general–purpose register.
It is the type of the instruction that determines that
a register number refers to
a floating–point register rather than a general–purpose register.
Consider the following code.
R4 EQU 4
AR R4,R4 ADD REGISTER, REFERING TO A
GENERAL-PURPOSE
INTEGER REGISTER.
ADR R4,R4 ADD DOUBLE
PRECISION FLOAT REGISTER,
REFERING TO THE
FLOATING POINT REG.
Conversion Between Single and Double Precision
Recall that the structure of the two precisions is
quite similar.
|
Byte |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
E |
Sign & |
24 bit fraction |
|
|||||
|
D |
Sign & |
56 bit fraction |
||||||
To
convert single–precision floating point to double–precision floating–point,
just add eight hexadecimal zeroes at the end.
Thus single precision 42 78 E8 00
becomes double precision 42 78 E8 00 00 00
00 00
Conversion from double–precision to single–precision
might involve loss of
accuracy. It might be done by rounding
or truncation.
Thus, double precision 42 78 E8 04 A8 00 00 00
might become 42 78 E8 04
or it might become 42 78 E8 05
Loading a
Floating Point Register
When a floating–point register is loaded from a
double–precision floating–point
value, the process is simple: copy the 64–bit value into the 64–bit register.
When a floating–point register is loaded from a
single–precision floating–point
value, the process involves implicit conversion to double precision as shown
above.
The 32–bit value represented by the single–precision
float is loaded into the leftmost
32 bits of the floating point register and the right 32 bits are set to 0.
Consider the process of loading the decimal number
123.90625, represented as
42 78 E8 00
into a floating point register.
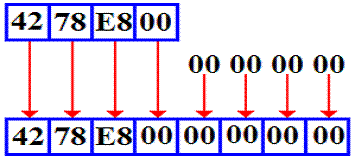
The value stored in the floating–point register is 42 78 E8 00 00 00
00 00,
which is the double–precision equivalent to the value loaded.
Range of the
Standards
Given that the base of the exponent is 16, the range
for these IBM formats is impressive.
The range is from somewhat less than 16–64
to a bit less than 1663.
Note
that 1663 = (24)63
= 2252, and
16–64 = (24)–64
= 2–256 = 1.0 / (2256)
Recall
that log10(2) = 0.30103.
Using
this, we compute the maximum number storable at about
(100.30103)252 » 1075.86 » 9·1075.
We
may approximate the smallest positive number at 1.0 / (36·1075) or about 3.0·10–77.
The
following non–negative real numbers can be represented in this standard:
X = 0.0 and
3.0·10–77 < X < 9·1075.
Precision of
the Standards
The precision is dependent on the format used,
depending on the
number of bits used to represent the fraction.
We can summarize the precision for each format as
follows.
Single
precision F = 24 1 part in 224.
Double
precision F = 56 1 part in 256.
Extended
precision F = 120 1 part in 2120.
The first power of 2 is easily computed; we use
logarithms to approximate the others.
224 =
16,777,216
256 » (100.30103)56 = 1016.85 » 9·1016.
2120 » (100.30103)120 = 1036.12 » 1.2·1036.
Summary
|
Format |
Type |
|
Precision |
|
Single Precision |
E |
3.0·10–77 < X < 9·1075 |
7 digits |
|
Double Precision |
D |
3.0·10–77 < X < 9·1075 |
16 digits |
|
Extended Precision |
L |
3.0·10–77 < X < 9·1075 |
36 digits |
Examples of
Floating Point Format (Page 1)
Example 1: True 0
The number 0.0, called “true 0” by IBM, is stored as
all zeroes.
In single precision it would be 0000 0000.
In double precision it would be 0000 0000
0000 0000.
Example 2: Positive exponent and positive fraction.
The
decimal number is 128.50. The format
demands a representation in the
form X·16E, with
0.625 £ X < 1.0.
As
128 £ X < 256, the number
is converted to the form X·162.
Note that 128 = (1/2)·162 = (8/16)·162 , and 0.5 = (1/512)·162 = (8/4096)·162.
Hence, the value is 128.50 = (8/16 + 0/256 + 8/4096)·162; it is 162·0x0.808.
The
exponent value is 2, so the characteristic value is either 66 or 0x42 = 100
0010. The
first two hexadecimal digits in the eight digit representation are formed as
follows.
|
Field |
Sign |
Characteristic |
||||||
|
Value |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
Hex value |
4 |
2 |
||||||
The fractional part comprises
six hexadecimal digits, the first three of which are 808.
The number 128.50 is represented as 4280 8000.
Examples of
Floating Point Format (Page 2)
Example 3: Positive exponent and negative fraction.
The
decimal number is the negative number –128.50.
At this point, we would normally
convert the magnitude of the number to hexadecimal representation. This number has the
same magnitude as the previous example, so we just copy the answer; it is 162·0x0.808.
We
now build the first two hexadecimal digits, noting that the sign bit is 1.
|
Field |
Sign |
Characteristic |
||||||
|
Value |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
Hex value |
C |
2 |
||||||
The number 128.50 is
represented as C280 8000.
Note that we could have obtained this value just by adding 8 to the first hex
digit.
Examples of
Floating Point Format (Page 3)
Example 4: Negative exponent and positive fraction.
The
decimal number is 0.375. As a fraction,
this is 3/8 = 6/16. Put another way, it
is
160·0.375 = 160·(6/16). This is in the required
format X·16E, with
0.625 £ X < 1.0.
The
exponent value is 0, so the characteristic value is either 64 or 0x40 = 100
0000. The
first two hexadecimal digits in the eight digit representation are formed as
follows.
|
Field |
Sign |
Characteristic |
||||||
|
Value |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Hex value |
4 |
0 |
||||||
The fractional part comprises six hexadecimal digits,
the first of which is a 6.
The number 0.375 is represented in single precision as 4060 0000.
The number 0.375 is represented in double precision as 4060 0000 0000 0000.
Examples of
Floating Point Format (Page 4)
Example 5: A Full Conversion
The number to be converted is 123.45. As
we have hinted, this is a non–terminator.
Convert the integer part.
123 / 16 = 7 with remainder 11 this is hexadecimal digit B.
7 / 16 = 0
with remainder 7 this is hexadecimal digit 7.
Reading bottom to top, the integer part converts as 0x7B.
Convert the fractional part.
0.45 · 16 = 7.20 Extract the 7,
0.20 · 16 = 3.20 Extract the 3,
0.20 · 16 = 3.20 Extract the 3,
0.20 · 16 = 3.20 Extract the 3, and so on.
In
the standard format, this number is 162·0x0.7B33333333…...
Examples of
Floating Point Format (Page 5)
Example 5: A Full Conversion (Continued)
The exponent value is 2, so the characteristic value is either 66 or 0x42 = 100
0010.
The first two hexadecimal digits in the eight digit representation are formed
as follows.
|
Field |
Sign |
Characteristic |
||||||
|
Value |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
Hex value |
4 |
2 |
||||||
The number 123.45 is represented in single precision
as 427B 3333.
The number is represented in double precision as 427B 3333 3333 3333.
Example 6: One in “Reverse”
We are given the single precision
representation of the number. It is 4110 0000.
What is the value of the number stored?
Begin by examination of the first two hex digits.
|
Field |
Sign |
Characteristic |
||||||
|
Value |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Hex value |
4 |
1 |
||||||
The sign bit is 0, so the
number is positive. The characteristic
is 0x41, so the exponent is
1 and the value may be represented by X·161.
The fraction field is 100 000, so the value is 161·(1/16) = 1.0.
More On DC (Define Constant)
The general format of the DC statement is as follows.
|
Name |
DC |
dTLn
‘constant’ |
The name is an optional entry, but required if the program is to refer
to
the field by name. The standard column
positions apply here.
The declarative, DC, comes next in its standard
position.
The entry “dTLn” is read as
follows.
d is the optional
duplication factor. If not specified, it
defaults to 1.
T is the required type specification; usually
either E and D.
Note that the data actually
stored at the location does not need to be
of this type, but it is a good
idea to restrict it to that type.
L is an optional length of the data field in bytes.
The ‘constant’ entry is required and is used to
specify a value.
If the length attribute is omitted, the length is specified implicitly by this
entry.
Again, it is rarely desirable to specify a length for the E and D data
types.
Examples of Floating–Point Declaratives
Here are some examples of floating–point declaratives.
FL1 DS E This defines a 4–byte storage area,
aligned
on a fullword
boundary. Presumably, it
will store Single
Precision Data.
DL1 DS D An 8-byte storage
area, aligned on a double
word boundary. It could store data in
Double Precision format.
FL2 DC E‘12.34’ Define a
single precision value.
FL3 DC E‘-12.34’ The negative
of the above value.
DL2 DC D‘0.0’ The constant
0.0, in double precision.
DL3 DS D‘0.0’ Just another
storage allocation.
Value is not
initialized.
‘0.0’ is just a
comment.
Load Instructions
The
Load Instructions
The load instructions load a 64–bit floating point
register from either storage or
another floating–point register. The
valid register numbers are 0, 2, 4, or 6.
LE R1,D2(X2,B2) Load R1 single precision from memory
Operand 2 is an
aligned fullword;
its address is a multiple of 4.
LD R1,D2(X2,B2) Load R1 double precision from memory
Operand 2 is an
aligned double word;
its address is a
multiple of 8.
LER R1,R2 Load the leftmost 32 bits of R1
from the leftmost 32
bits of R2.
LDR R1,R2 Load the 64-bit register R1 from
the 64-bit register
R2.
The first two instructions are type RX and the last two are type RR.
Type RX Floating–Point Loads
The opcodes for the two type RX instructions are as
follows:
LE X‘78’ LD X‘68’
Each is a four–byte instruction of the form OP R1,D2(X2,B2).
|
Type |
Bytes |
Operands |
1 |
2 |
3 |
4 |
|
RX |
4 |
R1,D2(X2,B2) |
OP |
R1 X2 |
B2 D2 |
D2D2 |
The first byte contains the 8–bit instruction code.
The second byte contains two 4–bit fields, each of which encodes a
register number.
R1
is the floating point register to be loaded.
X2 is the
general–purpose register used as an index register.
The third and fourth bytes contain an address in the standard
base/displacement
with index register format.
The load instructions do not set any condition code.
Type RR Floating–Point Loads
The opcodes for the two type RR instructions are as
follows:
LER X‘38’ LDR X‘28’
The object code format for these type RR instructions
follows the standard.
Each is a two–byte instruction of the form OP R1,R2.
|
Type |
Bytes |
Operands |
|
|
|
RR |
2 |
R1,R2 |
OP |
R1
R2 |
The first byte contains the 8–bit instruction code.
The second byte contains two 4–bit fields, each of which
encodes a register number.
This instruction format is used to process data
between registers.
The Store Instructions
The
Store Instructions
There are two store instructions for storing either
the leftmost 32 bits or all 64 bits
of the 64 bit floating–point registers.
Again, the valid register numbers are 0, 2, 4, or 6.
as a single precision
result into the
aligned fullword
address.
STD R1,D2(X2,B2) Store the 64 bits of register R1 as a
double precision result
into the aligned
double word address.
The opcodes for these two instructions are as follows: STE X‘70’ STD X‘60’.
Each is a four–byte instruction of the form OP R1,D2(X2,B2).
|
Type |
Bytes |
Operands |
1 |
2 |
3 |
4 |
|
RX |
4 |
R1,D2(X2,B2) |
OP |
R1 X2 |
B2 D2 |
D2D2 |
The
first byte contains the 8–bit instruction code.
The second byte contains two 4–bit fields, each of which encodes a register
number.
The third and fourth bytes contain an address in the standard base/displacement
with
index register format.
Sample Code
LOAD1 LE 0,FL1 LOAD FP REG
0 FROM ADDRESS FL1
LOAD2 LD 2,FL2 LOAD DOUBLE
PRECISION
LOAD3 LER 4,0 COPY SINGLE PRECISION INTO FP REG 4
LOAD4 LDR 6,2 COPY DOUBLE PRECISION INTO FP REG 6
STORE1 STE 6,FL3 STORE THE
SINGLE PRECISION INTO FL3
STORE2 STD 6,FL4 STORE
DOUBLE PRECISION INTO FL4
FL1 DC E‘123.45’ A SINGLE PRECISION FLOATING POINT
CONSTANT. ADDRESS IS
MULTIPLE OF 4.
FL2 DC D‘45678.90’ A DOUBLE PRECISION
FLOATING POINT
CONSTANT. ADDRESS IS MULTIPLE OF 8
FL3 DS E JUST RESERVE AN ALIGNED FULLWORD
FL4 DS D
RESERVE AN ALIGNED DOUBLE WORD.
The DS E and DC E declaratives align the address of the memory area as
a multiple of 4.
The DS D and DC D declaratives align the address of the memory area as
a multiple of 8.
Addition and Subtraction
There are four distinct addition instructions and four
distinct subtraction instructions
for normalized floating–point numbers.
These instructions are as follows:
|
Mnemonic |
Operation |
Opcode |
Operand
Format |
|
AE |
Add
single precision |
7A |
R1,D2(X2,B2) |
|
AD |
Add
double precision |
6A |
R1,D2(X2,B2) |
|
AER |
Add
register single precision |
3A |
R1,R2 |
|
ADR |
Add
register double precision |
2A |
R1,R2 |
|
SE |
Subtract
single precision |
7B |
R1,D2(X2,B2) |
|
SD |
Subtract
double precision |
6B |
R1,D2(X2,B2) |
|
SER |
Subtract
register single precision |
3B |
R1,R2 |
|
SDR |
Subtract
register double precision |
2B |
R1,R2 |
Subtraction
functions by changing the sign of the second operand and then performing
an addition.
The first
step in each is ensuring that the characteristics of both operands are
equal. If
unequal, the field with the smaller characteristic is adjusted by shifting the
fraction to
the right and incrementing the characteristic by 1 until the characteristics
are equal.
Addition Example: Adjusting the Characteristic
Here is an
example of adjusting the characteristic.
Characteristic Fraction
41 29000 = 41 29000
40 12000 = 41 01200
41 2A200
Suppose that the fraction overflows. If that happens, the fraction is shifted
right by one
hexadecimal digit and the characteristic is incremented by 1. This last operation is
called normalization, in that it returns the result to the expected normal
form.
Characteristic Fraction
41 940000
41 760000
41 10A0000 which
becomes 42 10A000.
Recall that in hexadecimal addition we have 9 + 7 =
10.
Multiplication
There are four distinct floating–point multiplication
operations.
|
Mnemonic |
Action |
Opcode |
Operands |
|
ME |
Multiply
single precision |
7C |
R1,D2(X2,B2) |
|
MD |
Multiply
double precision |
6C |
R1,D2(X2,B2) |
|
MER |
Multiply
single (register) |
3C |
R1,R2 |
|
MDR |
Multiply
double (register) |
2C |
R1,R2 |
In each,
the first operand specifies a register that stores the multiplicand and,
after the multiplication, stores the product.
The operation normalizes the product, which in all
cases is a double–precision result.
Sample code segment
M1 LE 2,MULTCAN1 LOAD FIRS MULTIPLICAND
ME
2,MULTIPLIER
DO A MULTIPLICATION
LE 4,MULTCAN2 LOAD ANOTHER VALUE
MER 4,2 REG 4 GETS THE PROCUCT OF
THE THREE
VALUES.
Division
There are four distinct floating–point division operations.
|
Mnemonic |
Action |
Opcode |
Operands |
|
DE |
Divide
single precision |
7D |
R1,D2(X2,B2) |
|
DD |
Divide
double precision |
6D |
R1,D2(X2,B2) |
|
DER |
Divide
single (register) |
3D |
R1,R2 |
|
DDR |
Divide
double (register) |
2D |
R1,R2 |
In
each, the first operand specifies a register that stores the dividend and,
after the division, stores the quotient.
There is no remainder.
The
operation normalizes the quotient, which in all cases is a double–precision
result.
Sample code segment
D2 LD 2,DIVIDND1 LOAD FIRST DIVIDEND
DD
2,DIVSOR
FIRST DIVISION
LD 4,DIVIDND2 LOAD SECOND DIVIDEND
DDR 4,2 ANOTHER DIVISION
DIVIDND2 / (DIVIDND1 / DIVSOR)
or (DIVIDND2 *
DIVSOR)/ DIVIDND1
Comparison
There are four distinct floating–point division
comparison operations.
|
Mnemonic |
Action |
Opcode |
Operands |
|
CE |
Compare
single precision |
79 |
R1,D2(X2,B2) |
|
CD |
Compare
double precision |
69 |
R1,D2(X2,B2) |
|
CER |
Compare
single (register) |
39 |
R1,R2 |
|
CDR |
Compare
double (register) |
29 |
R1,R2 |
In
each, the comparison sets the condition codes as would be expected for
comparisons in the other
formats. Each operation proceeds as a
modified subtraction. The characteristic
fields of the two
operands are checked, and the smaller exponent is incremented while right
shifting its fraction
(denormalizing the number, but preserving its value) before the comparison.
If
both operands have fractions that are zero (all bits in the field are 0), the
result is
declared to be equal without consideration of either the exponent or the sign.
The
single precision operations compare only the leftmost 32 bits in each value.