Support for
General Recursion
In this
lecture, we shall consider the support for the general case of recursion.
We shall
also restrict the implementation somewhat in order to
illustrate the important points without “going overboard” on the complexities.
In
FORTRAN terms, there are two classes of procedures.
Functions Those procedures that return a value
and, in the ideal case, have
no effect on
the calling program other than passing that value.
Subroutines Those
procedures that perform general actions and optionally
can alter a
number of variables in the calling program.
In this
lecture, everything will be called a procedure.
The
issues to be addressed in providing for recursion are as follows:
1. Passing
the return address.
2. Passing
the arguments to the procedure.
3. Handling
variables declared locally in the procedure, whose scope does not extend
beyond that procedure; they
cannot be used directly in the calling program.
Outline of
the Lecture
We shall
cover the topics in roughly the sequence below.
1. The
assumptions defining the context in which recursion is used.
2. The
idea of generalizing the stack to provide efficient support for recursion.
3. Allocation
of areas of the stack for arguments to the procedure and
variables local to the
procedure.
4. Declaration
of static variables with scope local to the procedure. In Java, these
may be called class variables.
5. Call
by value and call by reference. Writing
code to access each of these
as stored on the stack, and how
to modify arguments passed by reference.
6. A
few modest proposals for increasing the security of the run–time system,
and consideration of the
difficulties in their implementation.
Assumption
1: The Linkage Code is Consistent
The
high–level description of the procedure linkage problem is as follows.
1. The
calling program invokes the procedure.
a) It
places the return address on the stack.
b) It
places the arguments on the stack.
2. The
called procedure receives control.
a) It
modifies the stack to create room for its variables with local scope.
b) It
accesses the arguments and uses them as specified.
Thus we
must have two sections of code that must be consistent. Design of the
calling code will force the design of the receiving code.
In particular,
the handling of arguments passed by value must be different from
that for arguments passed by reference.
In this
lecture, my assumption is that the assembly language I write for each section
will be emitted by a well–designed compiler, so that consistency is enforced.
Assumption 2:
The Executable Code is Loaded Statically
The
assumption here is that each block of code (main program, subroutine, function,
etc.)
is loaded into memory once, and that this loading is at an address that remains
fixed
during the execution of the program.
Variables
corresponding to data declarations within a procedure are static.
Consider
the following code, which uses a number of externally declared labels.
It might
be modified into a print routine that records the count of pages printed.
A10LOOP MVC
DATAPR,RECORDIN MOVE INPUT
RECORD
LH R7,PAGENUM LOAD THE OLD PAGE NUMBER
AH R7,=H‘1’ INCREMENT BY 1
STH R7,PAGENUM
SAVE THE NEW COUNT
PUT
PRINTER,PRINT PRINT THE RECORD
BR R8 R8
HOLDS RETURN ADDRESS
PAGENUM DC H‘0’ THE PAGE COUNTER
The
label PAGENUM, as used above,
should be considered a local variable that is
declared statically. There are two
interesting features of such variables.
1. It
will retain its value across invocations.
2. All
instances of the procedure access the same location when accessing
the value denoted by PAGENUM.
The Memory
Map for Static Allocation
Here is
a sample memory layout for a MAIN program and a procedure PROC1.
This is to be considered a map of the computer
memory at the time this program is executing.
The data
areas that are labeled as “ARGS” are
statically allocated.
Each
reference to a label in one of these refers to
the same address in computer memory.
That
address is determined when the program is loaded.
This
arrangement will not work for recursion, even if
the return addresses are handled by a stack.
The Problem
with Static Allocation
Consider
the following code fragments related to the factorial program.
It is
easier to see this problem when DOFACT is written in a higher level language.
Here is
a plausible implementation.
Integer DoFact
(Integer N) ;
var
M : Integer ; // A local variable, declared static
Begin
If (N <= 1) Then DoFact := 1
Else
Begin
M = N;
// Save the current value
DoFact := M * DoFact(N – 1);
End
End
If the
storage allocation for M is on the stack, this will work well.
If the
storage allocation for M is static, this fails.
Static
Allocation: An Execution Trace
Suppose
that the label M is statically allocated.
Here is an execution trace.
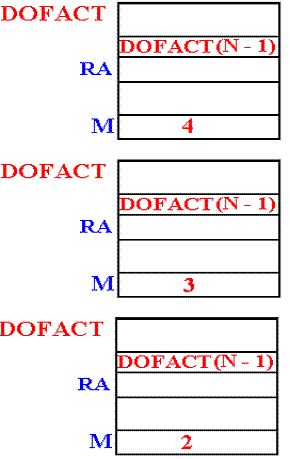DOFACT (4) is called and begins execution.
The
value 4 is stored in the location associated with
label M. DOFACT (3) is called
DOFACT
(3) begins execution.
The
value 3 is stored in the location associated with
label M, overwriting the previous value.
DOFACT
(2) begins execution
The
value 2 is stored in the location associated with
label M, overwriting the previous value.
Assume
that DOFACT (1) does not store a value.
Our result is FACT(4) = 2·FACT(3) = 2·2·FACT(2) = 2·2·2·FACT(1) = 2·2·2 = 8.
Assumption 3:
No Use of Global Variables
The
problem of global variables is illustrated by the following code fragment,
which is written in a variant of PASCAL.
Program
var
X, Y : Real ;
Procedure Sub_1;
var
Y, Z : Integer ;
Begin
// Body of Sub_1
End ;
Begin
// Body of main.
End ;
Within
procedure
to procedure Sub_1, is not visible within
Within
procedure Sub_1, variables X, Y, and Z all have meaning, though the
variable Y denotes the local copy.
The
problem is that of providing procedure Sub_1 with a reference to global
variable X,
if it is not passed as an argument.
While this is easy, I choose to ignore this issue.
Stack
Support for Generalized Recursion
In this
lecture, I shall define one plausible stack organization to support recursive
procedures with arguments and local variables.
Again, I
shall not consider the problem of access to global variables.
The
structure of the stack is dictated by how it is used in the context of calling.
1. A
procedure will be executing. It accesses
all of its local variables via the stack.
At this
point, this procedure calls another.
2. Each
of the arguments is pushed onto the stack.
3. The
return address is pushed onto the stack.
4. The
new procedure is invoked.
5. The
new procedure allocates space on the stack for its local variables.
This
sequence dictates the structure of the stack.
That
part of the stack directly used by a procedure is called an “activation record”.
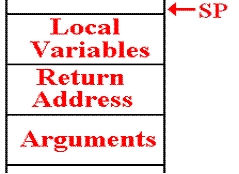
Implied
Structure of the Stack
For each
procedure, here is the form of the activation record, as seen on the stack.
I should
first note that there are many ways to structure the activation record, this is
just my way that I find easiest for presentation to this class.
Here is
the form of the stack upon entry to a procedure.
Here is
the form of the stack after the procedure has allocated space for local
variables.
A New Way to
Access the Stack
At this
point, I restate the design decision that only 32–bit fullwords are placed
onto the stack. Effectively, this limit
values to four types.
1. The
contents of a general purpose register.
2. The
contents of a 32–bit fullword.
3. The
contents of a 16–bit halfword, sign extended to a fullword.
4. Any
address, treated as a 32–bit fullword.
The
traditional stack structure is accessed one item at a time using only PUSH and
POP operations. For this use, it will be
necessary to devise new stack operations.
Block allocation will be used to reserve a number of slots in the stack for use in
either passing arguments or in providing space for local variables.
Block deallocation will be used to move the stack pointer without necessarily
popping the values from the stack.
Block
deallocation is used on return from a procedure. In essence, we just
change the value of the stack pointer directly.
A Slight
Redefinition of the Stack
In my
earlier work on a stack, I had become interested in an Abstract Data Type
definition, in which the value of the SP (Stack Pointer) is stored in the
structure.
I now
find it useful to allocate a register as the SP.
Here are
two code fragments that show the new definition of the stack.
Here are
some equates that define new uses for general purpose registers.
RVAL
EQU 3 // FUNCTION RETURN VALUE
SP
EQU 4 // STACK POINTER
FP
EQU 5 // ANOTHER USEFUL
POINTER.
The
stack itself is now just an allocation of memory. Let’s make it bigger.
THESTACK DC 512F’0’ THE STACK NOW HOLDS 512 FULLWORDS
We still
require some code to initialize the stack.
The key code might be
LA SP,THESTACK // Load address of the stack
Sample
Procedure
First, I
want to postulate a recursive subroutine and describe its key features in
a pseudo–language. Since I do not know
what it does, it is called DOWHAT.
Recall
that I prefer UPPER CASE letters, as I find them easier to read.
Here is
the essential declaration.
PROCEDURE DOWHAT ( INT
X ;
// PASSED BY REFERENCE
INT Y ;
// PASSED BY VALUE
INT Z ) ; // PASSED BY VALUE
// LOCAL VARIABLES
INT L1, L2, L3, L4
Recall
the argument passing mechanisms.
It would
make sense to have code such as X = Y + Z; the value of X changes.
One
could write code such as Y = X + Z; this would have effect only in DOWHAT.
Conventions
for Argument Handling
Recall
that the goal of the compiler designer is to convert a high–level language
statement into a sequence of assembly language statements having the same
effect.
The
requirement is to place the arguments onto the stack.
For
this, it will be convenient to use a standard STKPUSH.
What is
the sequence of pushing the arguments? Is
it X, Y, Z or Z, Y, X?
Are they
pushed right to left or left to right.
All that matters is consistency.
Arbitrary choices:
1. I
shall push the arguments right to left.
2. Because
I find it interesting, I shall also push the argument count.
PUSH (Value of Z) Called by value
PUSH (Value of Y) Called by value
PUSH (Address of X) Called by reference
PUSH (3) Three arguments passed.
Calling
DOWHAT
For now,
we assume that locations X, Y, and Z have declarations of the type.
X DC
F‘0’
Y DC
F‘0’
Z DC
F‘0’
Here is
the code involved in an invocation of DOWHAT.
STKPUSH Z Push value of Z
STKPUSH Y Push value of Y
STKPUSH X,A Push address of X
STKPUSH =F‘3’ Push the constant value 3
STKPUSH A1,A Push the return address
B DOWHAT Now call the
procedure.
A1 Return Address: this code next.
My preference
here is to use the explicit push operation, rather than a
block allocation for the stack and direct access to its members.
The State of
the Stack
We
consider the state of the stack at this point.
It can be at one of two
equivalent points.
1. Just
before DOWHAT has been called.
2. Just
after DOWHAT has been called, but before any of its code has executed.
DOWHAT
Allocates Its Local Variables
At this
point, I wish to introduce a FP (Frame Pointer) and warn that my use of
this is almost certainly to be non–standard and have flaws that are not
apparent to me.
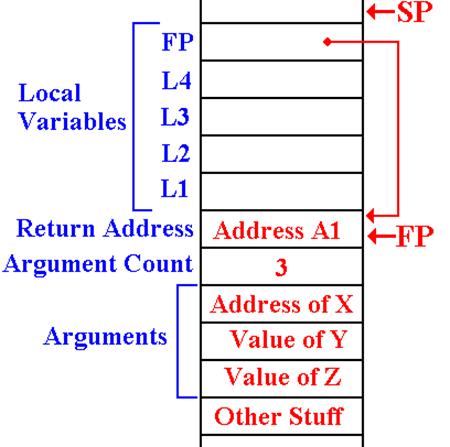The four local variables are allocated on the stack.
Here, I
arbitrarily set the FP to indicate the location of the return address.
I also
elect to store the current value of FP as a local variable.
This is
the status of the stack during any execution of DOWHAT.
Entry Code
for DOWHAT
The
entry code for DOWHAT is the code to allocate the local variables, define
the value of the FP, and store a local copy for later use.
For four
local variables we want to allocate five locations on the stack.
Here is the situation on entry.
Here is
the code to allocate the local variables.
LR FP,SP // SET UP THE FRAME POINTER
SH FP,=H‘4’ // IT NOW POINTS TO THE RETURN ADDR.
AH SP,=H‘20’ // MOVE THE STACK POINTER
ST FP,20(0,FP) // SAVE THE LOCAL COPY
DOWHAT
Accesses Its Arguments
Recall
the status of the stack when DOWHAT is called.
Here, I ignore the local
variables and focus on the arguments.
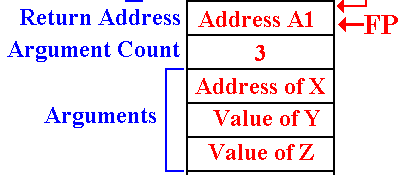
The
value of the first argument will be accessed somewhat as follows.
To get
the value: L R8,–8(0,FP) // Get the
address
L R9,0(0,R8) // Get the value
To store
a value: L R8,–8(0,FP) // Get the
address
ST R9,0(0,R8) // Store the new value
Others are
accessed by value, as in L R9,–12(0,FP).
DOWHAT
Returns
For the
moment, I skip what the routine might do and indicate how it returns.
The
first step in a return is to de–allocate the local variables. This is easily
done by giving the stack pointer a new value.
Here is the code
LR SP,FP //
Change the value and thus remove
// access to the local variables.
LR R9,-4(0,SP)
// Get the argument count
AH R9,=H‘1’ //
Add 1 to the value.
SLA R9,2 // Multiply by 4; get byte offset
SR SP,R9 //
Adjust stack pointer. It now
// points to the
first word allocated
// for this
invocation of DOWHAT.
LR R9,0(0,FP) // Get the return address
DOWHAT Calls
Itself
Suppose
that DOWHAT calls itself recursively with something like
DOWHAT (L1, L2, L3)
A2 Next instruction in DOWHAT
How do
we handle the call and return?
First,
we need to look at the stack at the time that DOWHAT calls itself.
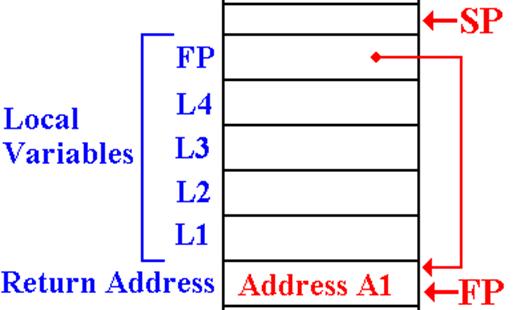Recall that L3 is pushed first.
The code for this might be .
STKPUSH 12,(0,FP)
STKPUSH 8,(0,FP)
STKPUSH 4,(0,FP),A
LH R9,=H‘3’
STKPUSH R9,R
STKPUSH A2,A
B DOWHAT
DOWHAT
Processes a Return
Here we
consider a return from another procedure, perhaps a recursive call.
Consider
the code just above.
DOWHAT (L1, L2, L3)
A2 Next instruction in DOWHAT
What
happens at address A2? Recall the status
of the “top part” of the stack.
All we do is to locate where the FP is stored and restore its value.
L FP,-4(0,SP)
We have
now returned to the
execution environment
appropriate for this
invocation of DOWHAT.