Chapter 8: Addressing in the IBM S/370

All stored–program computers run programs that have been converted to binary machine code and loaded into the primary memory.  The presence of virtual memory on most modern computers is just a variation of that scheme; the basic idea remains the same.

Fundamental to the execution of a loaded computer program is the association of an absolute address in primary memory for every line of code and data item.  Again, the presence of virtual memory adds a variation on this scheme, but does not change the basic idea.

There are two types of addresses in a virtual memory system: the logical address issued by the program and the physical address used for actual memory reference.  In fact, the basic definition of virtual memory is that it is a mechanism for decoupling logical addresses from physical addresses.  In a virtual memory system, the executing program calculates a logical address, and some mechanism (usually part of the Operating System) converts that logical address into a physical address that is used for the actual memory reference.

While it is a fact that almost every implementation of virtual memory makes use of a disk as a backing store, reading sections of the program and data into physical memory as needed, this is not an essential part of the definition.  As a matter of fact, it is possible (but very misleading) to claim that the early IBM mainframe computers supported virtual memory: the physical address was always the logical address.

This chapter discusses the mechanisms by which an executing S/370 assembler language program generates a logical address that will later be converted to a physical address.  While later models of the IBM Mainframe line, such as the current z/10, make use of considerably more complex mechanisms to generate logical addresses, the methods discussed here will still work in a program executing on these more modern systems.

Perhaps the major difference between the early and current models in the IBM Mainframe line is the size of logical address that can be generated.  There are three different phases of address generation: 24 bit, 31 bit, and 64 bit.  The progress in evolution of the address space is shown in the following table.

Address Space

Year

First Model

24 bits

1964

S/360 and early S/370

31 bits

1983

3081 processor running S/370–XA

64 bits

2000

zSeries model 900 running z/OS or z/VM

The curious reader might wonder why IBM elected to use a 31–bit address space rather than a 32–bit address space when it introduced S/370–XA.  The answer seems to have been a desire to maintain compatibility with some of the instructions on the S/360.

This chapter will focus exclusively on the mechanisms used to generate the 24–bit logical addresses in the S/360 and early S/370 models.  As suggested above, there are 2 reasons.

      1.   Programs written in this mode will still run on the modern zSeries servers.

      2.   This simpler scheme illustrates the methods used in all systems to generate
            addresses without getting lost in the complexity of a 64–bit address space.

 

The topics in this chapter include the following.

      1.      A review of 32–bit binary arithmetic, as described by IBM.

      2.      A characterization of the sixteen general–purpose registers in the
               System/370.  Which are really general purpose?

      3.      Control sections and their relation to address calculation.

      4.      Base register addressing.  Computing effective addresses.

      5.      Assigning and loading base registers.

32–bit binary arithmetic, as described by IBM.

The IBM System/370 architecture calls for sixteen general–purpose registers, numbered
0 through 15, or 0 through F in hexadecimal.  Each of these registers can store a 32–bit signed binary integer in two’s–complement form.  The range of these integers is
–231 to 231 – 1, inclusive, or  –2,147,483,648 through 2,147,483,6647.

The IBM standard calls for the bits in the registers to be numbered left to right.  Notice that this is not a standard used by other designs.  In particular, it is not used in the lecture
material for other courses.

In the IBM notation, bit 0 is the sign bit.  It is 1 for a negative number and 0 for a non–negative.  Consider a 32–bit integer.  In some terminology, bit 0 is said to be the sign bit and bits 1 – 31 are said to be data.  Thus, what is often called a 32–bit signed integer might be referenced in the IBM literature as a 31–bit integer.  This is not the way I would say it,
but it is the terminology we shall use for this course.

To be specific, consider an eight–bit integer, which can store –128 through 127 as a
two’s–complement signed integer.  All notations call for the bits to be numbered 0 through 7.  The bit labels would be as follows.

The IBM notation

Bit Number

0

1

2

3

4

5

6

7

Use

Sign

MSB

 

 

 

 

 

LSB

The More Common Notation

Bit Number

7

6

5

4

3

2

1

0

Use

Sign

MSB

 

 

 

 

 

LSB

For the IBM S/370 addressing scheme, there are two number systems that are significant.  Each is an unsigned number system, so that there are no negative values considered.  These systems are 12–bit unsigned integers and 24–bit unsigned integers.  Each of these systems is used in address computation.

The range of a 12–bit unsigned integer is from 0 through 212 – 1, or 0 through 4,095
inclusive, as 212 = 4,096.

The range of a 24–bit unsigned integer is from 0 through 224 – 1, or 0 through 16,777,215
inclusive, as 224 = 16,777,216.

The General Purpose Registers

The general–purpose registers in the System/370 are identified by number: 0 – 15, or
0 – F in hexadecimal.  Of these, only the ten registers 3 through 12 ( 3 – C in hexadecimal) can be used for any purpose.  The other six registers are “less general purpose” and should be used with caution.

Registers 0 and 1 can be used as temporary registers, but calls to supervisor routines will destroy their contents.

Register 2 can be used as a temporary and possibly as a base register.
The TRT (Translate and Test) instruction will change the value of this register.

Registers 13, 14, and 15 are used by the control programs and subprograms.

Each of the sixteen registers is identified by a four–bit binary number, or equivalently by a single hexadecimal digit.

Suggested convention:  Use register 12 as the single required base register.
The standard prefix code would contain the following sequence.

          BALR  12, 0
          USING *, 12

Within this scheme, only registers 3 through 11 (3 through B, in hexadecimal) are to be viewed as truly general–purpose.  All other registers have pre–assigned uses.

Recall that many programs will begin with some equate statements, in particular those that give more useable symbolic names to registers.  In this scheme, the above would appear as:

          R12   EQU 12         Synonym for 12

          Other declarations

          BALR  R12, 0
          USING *, R12

Base Register Addressing

The System/370 uses a common design feature that splits addresses into two parts:

      1.      A base address, stored in a specified base register. 
               In general, only registers 3 through 12 should be used as base registers.

      2.      A displacement, specifying the positive offset (in bytes) from the start
               of the section.  The System/370 uses a 12–bit number for this displacement.
               The displacement value is in the range 0 through 4095, inclusive.

The format of the address in this form is as follows:

| B | D D D |

where B is the single hexadecimal digit indicating the base register, and
“D D D” denotes the three hexadecimal digits used to specify the offset.

Suppose that general–purpose register 3 contains the value X’4500’.
The address reference 3507, interpreted as | 3 | 507 | refers to the address that is offset
X‘507’ from the value stored in the base register.  The base register is 3, with contents
X‘4500’, so the value is X’4500’ + X’507’ = X’4A07’  In hexadecimal 5 + 5 = A.

NOTE:   Register 0 cannot be used as a base register.  The assembler will interpret
                        the address | 0 | D D D | as no base register being used.

More on Register 0 As a Base Register

The bottom line is “Don’t try this (at home)”.  In other words, any attempt to use register 0 for anything other than temporary results is likely to cause problems.

As noted above, some addresses are given in the form | B | D D D |, where

      B is a hexadecimal digit indicating a base register, and

      D D D is a set of three hexadecimal digits indicating an offset in the range 0 – 4095.

If the object code generated has the form | 0 | D D D |, then no base register is used in
computing the address.  We shall use this later to load registers with positive constants.

One has another option that might force register 0 to be a base register.  We can start the program as follows.

         BALR R0, 0

         USING *, R0

While this MIGHT assemble correctly (I have no idea), it is most certainly a very bad idea.  Any call to a system procedure will disrupt the addressing.

Options: No Base Register vs. The Default Base Register

So far, we have considered only the object code form of a typical address.  We now “jump ahead” a bit and look at two typical instructions that use this address type.

One type of instruction, called “RS”,  used for register–to–storage instructions.

Such an instruction has source code of the form        OP R1,R3,D2(B2).

Such an instruction has object code of the form        OP R1R3 B2D2 D2D2.

We look at LM, an interesting example of this format.

LM R1,R3,S2 loads multiple registers in the range R1 – R3 from the memory
location specified by S2, the address of which will be in the form | B2 | D2 D2 D2 |.

We now interpret the following code fragment.

   BALR  R12, 0       Establish register R12 (X‘C’)

   USING *, R12       as the default base resister.

   LM R5,R7,S2        might have object code 98 57 C1 00.
                      This uses the default base register.

   LM R9,R11,S3(R3)   Use R3 as an explicit base register.
                      might have object code 98 9B 31 40. 

Object code such as 98 9B 0E 00 would call for use of an absolute address, not
computed from a base register.  For this example, it is likely to be bad code.

Rationale for Base Register Addressing

There are two advantages of base/displacement addressing.  One reason is still valid and one shows an interesting history.  Remember that the System/370 of the time admitted a 24–bit address space, with addresses ranging from 0 through 224–1 or 0 through 16,777,215.

A full 24–bit address would require 24 bits, or six hexadecimal digits, or three bytes.

The base register/displacement method of addressing allocates

                 4 bits to the base register

               12 bits to the displacement

In this method, an address requires 16 bits, or two bytes.  The instruction length is reduced because each address requires only two bytes rather than three.

One might infer that some of the System/360 and System/370 installations had very little memory.  Indeed, some of the early S/360 systems shipped with only 128 KB of memory.

Base Register/Displacement Addressing: Relocating the Code

The second major advantage of base/displacement addressing still applies today.

The system facilitates program relocatability.  Instead of assigning specific fixed storage addresses, the assembler determines each address relative to a base address.  At execute
time (after the program is loaded), the base address, which may be anywhere in storage, is loaded into a base register.”

The standard prefix code

         BALR 12, 0

         USING *, 12

may be translated as follows:

      1.      What is my address?

      2.      Load that address into register 12 and use it as an base address in that register.

The other option for relocating code is to use a relocating loader to adjust fixed
address references to reflect the starting address of the code.  This is also acceptable.

In the 1960’s, code that did not reference absolute addresses was thought to be superior.
Such code was called “position independent code”.

Base/Displacement vs. Indexed Addressing

Note the similarities with indexed addressing, in which the base is given by a variable and the offset is given by a register.  Systems that use the register contents as a base do so because the registers can store larger numbers than the bits in the machine code.

For example, the System/360 allocates only 12 bits for the displacement, which is combined with the contents of a register, which can be a 32–bit number.  The MIPS–32, a design from the mid 1980’s, also uses base/displacement addressing rather than indexed addressing.

In the MIPS–32 architecture, the displacement is a 16–bit signed integer, and the register values are 32–bit numbers.  This is basically the same idea, except that the displacement can be a negative number.  The range for the MIPS–32 is –32,768 through 32,767 inclusive.

Addressing: More Discussion

Here are some more examples of addressing using an index register and a base register.

All of these examples are taken from type RX instructions, which use indexing.

Each of these is a four–byte instruction of the form OP R1,D2(X2,B2).  The format
of the object code is OP R1X2 B2D2 D2D2.  Each byte contains two hexadecimal digits.

We interpret the 32–bit object code as follows.

      OP                   This is an eight–bit operation code.

      R1X2                This byte contains two hexadecimal digits, each of which is significant.

                              R1 denotes a register as the source or destination of the operation.

                              X2 denotes a general–purpose register to be used as an index register.

      B2D2 D2D2      This contains the argument address as a base register and displacement.

Remember that the displacement, given by three hexadecimal digits, is treated as a
12–bit unsigned integer.  In decimal, the limit is 0 £ Displacement £ 4095.

The general form by which an address is computed is
               Contents (Base Register) + Contents (Index Register) + Displacement.

Some instructions do not use index register addressing.

Addressing: Example 1

Here is some object code for analysis.

                        58 40 C1 23

The first thing to note is that the opcode, 58, is that for L, a Register Load.  This is a type RX instruction with object code of the form OP R1X2 B2D2 D2D2.

As noted above, OP = 58. 

We see that R1 = 4.  It is register 4 that is being loaded from memory.

We see that X2 = 0.  Indexed addressing is not used.

We also note that B2D2 D2D2 = C1 23, indicating an offset of X‘123’, or decimal 291, from the address value stored in general–purpose register 12 (hexadecimal C).

Suppose that the value in general–purpose register 12 is X‘2500’.  The effective
address for this instruction is then X‘2500’ + X‘123’ = X‘2623’.

 

Addressing: Example 2

Here is another example of object code.

                        58 A7 B1 25

The first thing to note is that the opcode, 58, is that for L, a Register Load.  This
is a type RX instruction with object code of the form OP R1X2 B2D2 D2D2.

As noted above, OP = 58. 

The hexadecimal digit for the register is A, indicating that register 10 is being loaded.
Recall that all of the digits in the object code are given in hexadecimal.

We see that X2 = 7, indicating that general–purpose register 7 is being used as an
index register. 

We also note that B2D2 D2D2 = B1 25, indicating an offset of X‘125’ from the
address value stored in general–purpose register 11 (hexadecimal B).

Suppose the following:                       Register 11 contains    X‘0012 4000’

                                                            The displacement is     X‘0000 0125’

                                                            Register 7 contains      X‘0000 0300’

The address is thus                                                                  X‘0012 4425’

An Aside: When Is It NOT An Address?

Let’s look at the standard form used for a base & displacement address.

| B | D D D |

Technically, the 12–bit unsigned integer indicated by D D D is added to the contents of the register indicated by B, and the results used as an address.  There are instructions in which the value so computed is just used as a value and not as an address.  Consider the instruction SLL   R4,1, which is a Shift Left instruction.  It is assembled as shown below.

            000018 8940 0001     00001    48          SLL   R4,1     

The base register is 0, indicating that no base register is used.  The “offset” is 1.

The value by which to shift is given as the sum, which is 1.

We could use a standard register to hold the value of the shift count, as in the following, which uses R8 to hold the shift count.

            000018 8940 8000     00001    48          SLL   R4,0(R8) 

NOTE:  This is a good example of not using a “base register” in order to generate
               an “absolute constant”, not relative to any address.  Here, the value is a count.

Assigning and loading base registers.

If the program is to use a base register for base register/displacement addressing, that register must be specified and provided with an initial value.

Again, the standard prefix code handles this.

         BALR 12, 0

         USING *, 12

If register 12 is used as a base register, it cannot be used for any other purpose.

In other words, your code should not reference register 12 explicitly.

We have two standards suggested for a base register.  The textbook uses register 3
and one of our examples uses register 12.  Pick one and use it consistently.

The Standard OS Prefix Code

Just to be complete, we show typical prefix code for running under OS.

This is taken from our lab 1.

LAB1    CSECT ,         COMMA REQUIRED IF COMMENT ON THIS STMT

**************************************************************

* STANDARD LINKAGE FOR A REUSABLE OS/MVS CSECT                

* THIS USES REGISTER 12 AS A BASE REGISTER.  THIS ASSUMES THAT

* THE SYMBOL R12 HAS BEEN DEFINED AS 12 IN A PRECEEDING EQU.  

************************************************************* 

      SAVE  (14,12)          SAVE CALLER'S REGS               

      BALR  R12,0            ESTABLISH                       

      USING *,R12            ADDRESSABILITY                  

      LA    R2,SAVEAREA      POINT TO MY LOWER-LEVEL SA      

      ST    R2,8(,R13)       FORWARD-CHAIN MINE FROM CALLER'S

      ST    R13,SAVEAREA+4   BACK-CHAIN CALLER'S FROM MINE   

      LR    R13,R2           SET 13 FOR MY SUBROUTINE CALLS  

**********************  BEGIN LOGIC  *************************

Relative Addressing

As we have seen, all symbolic addresses are based on variants of the concept of base address (stored in a base register) and an offset.  Note that the offset, encoded as a 12–bit unsigned integer, is always non–negative.  The possible offset values range from 0 through 4095.

We now introduce a way to reference a storage position relative to the symbolic address of another label.  This allows direct reference to unlabeled storage.

The form of a relative address is LABEL+N, where N is the byte offset of the desired storage relative to the symbolic address associated with LABEL.  Again, note the lack of spaces in the relative address.  This is important.

Consider the two data declarations.

            F1    DC F‘0’   A four–byte full-word.

            F2    DC F‘2’   Another full-word at address F1 + 4

Consider the following two instructions.  They are identical.

            L  R6, F2

            L  R6, F1+4

Relative Addressing: A More Common Use

The most common use of relative addressing is to access an unlabeled section of a multi–byte storage area associated with a symbolic address.  Consider the following very common declaration for card data.  It sets aside a storage of 80 bytes to receive the 80 characters associated with standard card input.

CARDIN  DS CL80

While only the first byte (at offset 0 from CARDIN) is directly named, we may use relative addressing to access any byte directly.  Consider this figure.

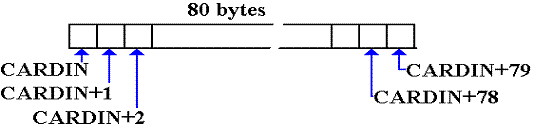
The second byte of input it is at address CARDIN+1, the third at CARDIN+2, etc.

Remember that the byte at address CARDIN+N is the character in column (N + 1) of the card.  Punched cards do not have a column 0, so valid addresses in this case range from
CARDIN through (CARDIN + 79).

Digression: Labels and Addresses

While we use labels to indicate addresses, we must recall that no label has an explicit data type associated with it when the program is run.  Each definition serves only to set aside memory.  The actual data type is associated with the assembly language operation.

Consider the following declarations and assume that the addresses are sequential.  In these examples, each is defined as hexadecimal, so that we can more easily see the problem.

FW1      DC X‘1234 ABCD’

HW1      DC X‘8888’         AT ADDRESS F1+4

HW2      DC X‘7777’         AT ADDRESS F1+6

The fullword at address FW1 has value X‘1234 ABCD’.

The halfword at address FW1 has value X‘1234’.

The halfword at address FW1+2 has value X‘ABCD’.

The halfword at address HW1 has value X‘8888’.

The halfword at address HW2 has value X‘7777’.

The fullword at address HW1 has value X‘8888 7777’.

Again, note that it does not matter that FW1 was intended to be a fullword or that each of
HW1 and HW2 to be a halfword.  It is the instruction that matters.

Explicit Base Addressing for Character Instructions

We now discuss a number of ways in which the operand addresses for character instructions may be presented in the source code.  One should note that each of these source code representations will give rise to object code that appears almost identical.  These examples are taken from Peter Abel [R_02, pages 271 – 273].

Assume that general–purpose register 4 is being used as the base register, as assigned at
the beginning of the CSECT.  Assume also that the following statements hold.

      1.   General purpose register 4 contains the value X‘8002’.

      2.   The label PRINT represents an address represented in base/offset form as 401A; that
            is it is at offset X‘01A’ from the value stored in the base register, which is R4.
            The address then is X‘8002’ + X‘01A’ = X‘801C’.

      3.   Given that the decimal number 60 is represented in hexadecimal as X‘3C’,
            the address PRINT+60 must then be at offset X‘01A’ + X‘3C’ = X‘56’ from
            the address in the base register.  X‘A’ + X‘C’, in decimal, is 10 + 12 = 16 + 6.

            Note that this gives the address of PRINT+60 as X‘8002’ + X‘056’ = X‘8058’,
            which is the same as X‘801C’ + X‘03C’.  The sum X‘C’ + X‘C’, in decimal, is
            represented as 12 + 12 = 24 = 16 + 8. 

      4.   The label ASTERS is associated with an offset of X‘09F’ from the value in the
            base register; thus it is located at address X‘80A1’.  This label references a storage
            of two asterisks.  As a decimal value, the offset is 159.

      5.   That only two characters are to be moved by the MVC instruction examples to be
            discussed.  Since the length of the move destination is greater than 2, and since the
            length of the destination is the default for the number of characters to be moved, this
            implies that the number of characters to be moved must be stated explicitly.

The first example to be considered has the simplest appearance.  It is as follows:

          MVC PRINT+60(2),ASTERS

The operands here are of the form Destination(Length),Source.
            The destination is the address PRINT+60.  The length (number of characters
            to move) is 2.  This will be encoded in the length byte as X‘01’, as the length
            byte stores one less than the length.  The source is the address ASTERS.

As the MVC instruction is encoded with opcode X‘D2’, the object code here is as follows:

Type

Bytes

Operands

1

2

3

4

5

6

SS(1)

6

D1(L,B1),D2(B2)

OP

L

B1 D1

D1D1

B2 D2

D2D2

 

 

 

D2

01

40

56

40

9F

The next few examples are given to remind the reader of other ways to encode
what is essentially the same instruction.

These examples are based on the true nature of the source code for a MVC instruction, which is MVC D1(L,B1),D2(B2).  In this format, we have the following.

      1.   The destination address is given by displacement D1 from the address stored in
            the base register indicated by B1.

      2.   The number of characters to move is denoted by L.

      3.   The source address is given by displacement D2 from the address stored in
            the base register indicated by B2.

The second example uses an explicit base and displacement representation of the destination address, with general–purpose register 8 serving as the explicit base register.

          LA  R8,PRINT+60     GET ADDRESS PRINT+60 INTO R8

          MVC 0(2,8),ASTERS   MOVE THE CHARACTERS

Note the structure in the destination part of the source code, which is 0(2,8).

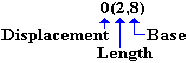
The displacement is 0 from the address X‘8058’, which is stored in R8.  The object code is:

Type

Bytes

Operands

1

2

3

4

5

6

SS(1)

6

D1(L,B1),D2(B2)

OP

L

B1 D1

D1D1

B2 D2

D2D2

 

 

 

D2

01

80

00

40

9F

The instruction could have been written as MVC 0(2,8),159(4), as the label
ASTERS is found at offset 159 (decimal) from the address in register 4.

The third example uses an explicit base and displacement representation of the destination address, with general–purpose register 8 serving as the explicit base register.

          LA  R8,PRINT        GET ADDRESS PRINT INTO R8

          MVC 60(2,8),ASTERS  SPECIFY A DISPLACEMENT

Note the structure in the destination part of the source code, which is 60(2,8).

The displacement is 60 from the address X‘801C’, stored in R8.  The object code is:

Type

Bytes

Operands

1

2

3

4

5

6

SS(1)

6

D1(L,B1),D2(B2)

OP

L

B1 D1

D1D1

B2 D2

D2D2

 

 

 

D2

01

80

3C

40

9F

The instruction could have been written as MVC 60(2,8),159(4), as the label
ASTERS is found at offset 159 (decimal) from the address in register 4.

Explicit Base Addressing for Packed Decimal Instructions

We now discuss a number of ways in which the operand addresses for character instructions may be presented in the source code.  One should note that each of these source code representations will give rise to object code that appears almost identical.  These examples are taken from Peter Abel [R_02, pages 273 & 274].

Consider the following source code, taken from Abel.  This is based on a conversion of a weight expressed in kilograms to its equivalent in pounds; assuming 1kg. = 2.2 lb.  Physics students will please ignore the fact that the kilogram measures mass and not weight.

         ZAP  POUNDS,KGS     MOVE KGS TO POUNDS

         MP   POUNDS,FACTOR  MULTIPLY BY THE FACTOR
         SRP  POUNDS,63,5    ROUND TO ONE DECIMAL PLACE

 

KGS      DC   PL3‘12.53’     LENGTH 3 BYTES

FACTOR   DC   PL2‘2.2’       LENGTH 2 BYTES, AT ADDRESSS KGS+3

POUNDS   DS   PL5            LENGTH 5 BYTES, AT ADDRESS KGS+5

The value produced is 12.53·2.2 = 27.566, which is rounded to 27.57.

The instructions we want to examine in some detail are the MP and ZAP, each of which
is a type SS instruction with source code format OP D1(L1,B1),D2(L2,B2).  Each of the two operands in these instructions has a length specifier.

In the first example of the use of explicit base registers, we assign a base register to
represent the address of each of the arguments.  The above code becomes the following:

         LA R6,KGS           ADDRESS OF LABEL KGS

         LA R7,FACTOR        ADDRESS

         LA R8,POUNDS

         ZAP 0(5,8),0(3,6)

         MP  0(5,8),0(2,7)

         SRP 0(5,8),63,5

Each of the arguments in the MP and ZAP have the following form:

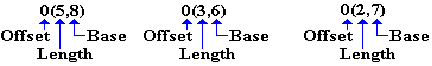
Recall the definitions of the three labels, seen just above.  We analyze the instructions.

ZAP 0(5,8),0(3,6)  Destination is at offset 0 from the address
                   stored in R8. The destination has length 5 bytes.

                   Source is at offset 0 from the address stored
                   in R6.  The source has length 3 bytes.

MP  0(5,8),0(2,7)  Destination is at offset 0 from the address
                   stored in R8. The destination has length 5 bytes.

                   Source is at offset 0 from the address stored
                   in R7.  The source has length 2 bytes.

But recall the order in which the labels are declared.  The implicit assumption that the labels are in consecutive memory locations will here be made explicit.

KGS      DC   PL3‘12.53’     LENGTH 3 BYTES

FACTOR   DC   PL2‘2.2’       LENGTH 2 BYTES, AT ADDRESSS KGS+3

POUNDS   DS   PL5            LENGTH 5 BYTES, AT ADDRESS KGS+5

In this version of the code, we use the label KGS as the base address and reference all other addresses by displacement from that one.  Here is the code.

         LA R6,KGS           ADDRESS OF LABEL KGS

         ZAP 5(5,6),0(3,6)

         MP  5(5,6),3(2,6)

         SRP 5(5,6),63,5

Each of the arguments in the MP and ZAP have the following form:

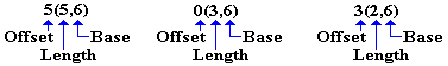
Recall the definitions of the three labels, seen just above.  We analyze the instructions.

ZAP 5(5,6),0(3,6)  Destination is at offset 5 from the address
                   stored in R6. The destination has length 5 bytes.

                   Source is at offset 0 from the address stored
                   in R6.  The source has length 3 bytes.

MP  5(5,6),3(2,6)  Destination is at offset 5 from the address
                   stored in R6. The destination has length 5 bytes.

                   Source is at offset 3 from the address stored
                   in R6.  The source has length 2 bytes.

In other words, the base/displacement 6000 refers to a displacement of 0 from the address stored in register 6, which is being used as an explicit base register for this operation.  As
the address in R6 is that of KGS, this value represents the address KGS.  This is the object code address generated in response to the source code fragment 0(3,6).

The base/displacement 6003 refers to a displacement of 3 from the address stored in register 6, which is being used as an explicit base register for this operation.  As the address in R6 is that of KGS, this value represents the address KGS+3, which is the address FACTOR.  This is the object code address generated in response to the source code fragment 3(2,6).

The base/displacement 6005 refers to a displacement of 5 from the address stored in register 6, which is being used as an explicit base register for this operation.  As the address in R6 is that of KGS, this value represents the address KGS+5, which is the address POUNDS.  This is the object code address generated in response to the source code fragment 5(5,6).

It is worth notice, even at this point, that the use of a single register as the base from which to reference a block of data declarations is quite suggestive of what is done with a DSECT, also called a “Dummy Section”.