Packed Decimal Format
Here, we discuss the packed decimal format, beginning with packed decimal constants.
A packed decimal constant is a
signed integer, with between 1 and 31 digits (inclusive).
The number of digits is always odd, with a 0 being prefixed to a constant of
even length.
A sign “half byte” or hexadecimal digit is appended to the
representation. The common
sign–representing hexadecimal digits are as follows:
C non–negative
D negative
F non–negative, seen in the results of a PACK instruction.
If a DC (Define Constant)
declarative is used to initialize storage with a packed decimal
value, one may use the length attribute.
Possibly the only good use for this would be to
produce a right–adjusted value with a number of leading zeroes.
For example DC PL6’1234’ becomes
|
00 |
00 |
00 |
01 |
23 |
4C |
Remember that each of these bytes holds two hexadecimal
digits, not the value
indicated in decimal, so 23 is stored as 0010 0011 and 4C as 0100
1100.
Some Examples and Cautions
Here are some examples of numbers being represented in packed decimal format.
DC P‘+370’ becomes 370C
DC P‘–500’ becomes 500D
DC P‘+92’ becomes 092C
Here are some uses that, while completely logical, might best be avoided. The problem with the first example is that the length in bytes is not sufficient to store the packed decimal number, so that the five leftmost digits are truncated. The second example shows the use of a DC declarative to define three constants in a manner that is difficult to read.
P1 DC PL2‘12345678’ is truncated to become 678C.
Why give a value only to remove most
of it?
PCON DC PL2‘123’,‘–456’,‘789’
This
creates three constants, stored as 123C, 456D, and 789C.
Only the first constant can be
addressed directly.
I would prefer the following sequence, with the labels P2 and P3 being optional.
P1 DC PL2‘123’
P2 DC PL2‘–456’
P3 DC PL2‘789’
More Examples
The
packed decimal format is normally considered as a fixed point format, with
a specified number of digits to the right of the decimal point. It is important to note that decimal points
are ignored when declaring a packed value.
When such are found in a constant, they are treated by the assembler as
comments.
Consider
the following examples and the assembly of each. Note that spaces have been
inserted between the bytes for readability only. They do not occur in the object code.
Statement Object Code Comments
P1 DC P‘1234’ 01 23 4C Standard expansion to 5 digits
P2 DC P‘12.34’ 01
23 4C The
decimal is ignored.
P3 DC PL4‘-12.34’ 00 01 23 4D Negative and lengthened to 4
bytes. Leading zeroes added.
P4 DC PL5’12.34’ 00
00 01 23 4C Five bytes in length.
This gives
2
bytes of leading zeroes.
P5 DC 3PL2‘0’ 00 0C 00 0C 00 0C Three values, each 2 bytes.
Explicit Base Addressing for Packed Decimal
Instructions
We now discuss a number of ways in which the operand addresses for character instructions may be presented in the source code. One should note that each of these source code representations will give rise to object code that appears almost identical. These examples are taken from Peter Abel [R_02, pages 273 & 274]. Consider the following source code, taken from Abel. This is based on a conversion of a weight expressed in kilograms to its equivalent in pounds; assuming 1kg. = 2.2 lb. Physics students will please ignore the fact that the kilogram measures mass and not weight.
ZAP POUNDS,KGS
MOVE KGS TO POUNDS
MP
POUNDS,FACTOR MULTIPLY BY THE
FACTOR
SRP POUNDS,63,5
ROUND TO
KGS DC
PL3‘12.53’ LENGTH 3 BYTES
FACTOR DC
PL2‘2.2’ LENGTH 2 BYTES, AT
ADDRESSS KGS+3
POUNDS DS
PL5 LENGTH 5 BYTES, AT
ADDRESS KGS+5
The value produced is 12.53·2.2 = 27.566, which is rounded to 27.57.
The
instructions we want to examine in some detail are the MP and ZAP,
each of which
is a type SS instruction with source code format OP D1(L1,B1),D2(L2,B2). Each of the two operands in these
instructions has a length specifier. In
the first example of the use of explicit base registers, we assign a base
register to represent the address of each of the arguments. The above code becomes the following:
LA R6,KGS ADDRESS OF LABEL KGS
LA R7,FACTOR ADDRESS
LA R8,POUNDS
ZAP 0(5,8),0(3,6)
MP
0(5,8),0(2,7)
SRP 0(5,8),63,5
Each of the arguments in the MP and ZAP have the following form:
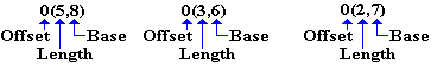
Recall the definitions of the three labels, seen just above. We analyze the instructions.
ZAP 0(5,8),0(3,6)
Destination is at offset 0 from the address
stored in R8. The
destination has length 5 bytes.
Source is at offset 0 from the
address stored
in R6. The source has length 3 bytes.
MP 0(5,8),0(2,7) Destination is at offset 0 from the address
stored in R8. The
destination has length 5 bytes.
Source is at offset 0 from the
address stored
in R7. The source has length 2 bytes.
But recall the order in which the labels are declared. The implicit assumption that the labels are in consecutive memory locations will here be made explicit.
KGS DC
PL3‘12.53’ LENGTH 3 BYTES
FACTOR DC
PL2‘2.2’ LENGTH 2 BYTES, AT
ADDRESSS KGS+3
POUNDS DS
PL5 LENGTH 5 BYTES, AT
ADDRESS KGS+5
In this version of the code, we use the label KGS as the base address and reference all other addresses by displacement from that one. Here is the code.
LA R6,KGS ADDRESS OF LABEL KGS
ZAP 5(5,6),0(3,6)
MP
5(5,6),3(2,6)
SRP 5(5,6),63,5
Each of the arguments in the MP and ZAP have the following form:
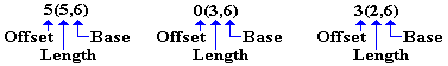
Recall the definitions of the three labels, seen just above. We analyze the instructions.
ZAP 5(5,6),0(3,6)
Destination is at offset 5 from the address
stored in R6. The
destination has length 5 bytes.
Source
is at offset 0 from the address stored
in R6. The source has length 3 bytes.
MP 5(5,6),3(2,6) Destination is at offset 5 from the address
stored in R6. The
destination has length 5 bytes.
Source
is at offset 3 from the address stored
in R6. The source has length 2 bytes.
In other
words, the base/displacement 6000 refers to a displacement of 0
from the address stored in register 6, which is being used as an explicit base
register for this operation. As
the address in R6 is that of KGS, this value represents the address KGS. This is the object code address generated in
response to the source code fragment 0(3,6).
The base/displacement 6003 refers to a displacement of 3 from the address stored in register 6, which is being used as an explicit base register for this operation. As the address in R6 is that of KGS, this value represents the address KGS+3, which is the address FACTOR. This is the object code address generated in response to the source code fragment 3(2,6).
The base/displacement 6005 refers to a displacement of 5 from the address stored in register 6, which is being used as an explicit base register for this operation. As the address in R6 is that of KGS, this value represents the address KGS+5, which is the address POUNDS. This is the object code address generated in response to the source code fragment 5(5,6).
It is worth notice, even at this point, that the use of a single register as the base from which to reference a block of data declarations is quite suggestive of what is done with a DSECT, also called a “Dummy Section”.
Packed Decimal: Moving Data
There are two instructions that might be used to move packed decimal data from one memory location to another. The preferred instruction is ZAP (Zero and Add Packed).
MVC S1,S2 Copy characters from location S2 to location S1
ZAP S1,S2 Copy the numeric value from location S2 to location S1.
Each of the two instructions can lead to truncation if the length of the receiving area, S1, is less than the source memory area, S2. If the lengths of the receiving field and the sending field are equal, either instruction can be used and produce correct results.
The real reason for preferring the ZAP instruction for moving packed decimal data comes when the length of the receiving field is larger than that of the sending field. The ZAP instruction copies the contents of the sending field right to left and then pads the receiving field with zeroes, producing a correct result.
The MVC instruction will copy extra bytes if the receiving field is longer than the sending field. The MVC instruction makes a left–to–right copy and will copy the required number of bytes, probably copying garbage. Consider the following example.
F1 DC P‘0000000’
stored as 0000 000C, this takes 4 bytes,
F2 DC P‘123’
stored as 12 3C, this takes 2 bytes.
F3 DC P‘4567’
stored as 04 56 7C, this takes 3 bytes.
Executing ZAP F1, F2 will cause F1 to be set to 0000 123C, which is correct.
Executing MVC F1, F2 will set F1 to 123C 0456, which not only is the wrong answer, but also fails to be in any recognizable packed decimal format.
Bottom line: Use the ZAP instruction to move packed decimal data.
Packed Decimal Data:
ZAP, AP, CP, and SP
We have four instructions with similar format.
ZAP S1,S2 Zero S1 and add packed S2 (This is the move discussed above)
AP S1,S2 Add packed S2 to S1
CP S1,S2 Compare S1 to S2, assuming the packed decimal format.
SP S1,S2 Subtract packed S2 from S1.
These are of the form OP D1(L1,B1),D2(L2,B2), which provide a 4–bit number representing the length for each of the two operands. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
OP |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The first byte contains the
operation code, which is X‘F8’ for ZAP, X‘F9’
for CP,
X‘FA’
for AP,
X‘FB’
for SP.
The second byte contains two hexadecimal digits, each representing an operand length.
Each
of L1 and L2 encodes one less than the length of the
associated operand. This
allows 4 bits to encode the numbers 1 through 16, but disallows arguments of
length 0.
The next four bytes contain two addresses in base register/displacement format.
Packed Decimal Data: Additional Considerations
For all four instructions, the second operand must be a valid packed field terminated with a valid sign. The usual values are ‘C’, ‘D’, and occasionally ‘F’, though the hexadecimal digits ‘A’, ‘B’, and ‘E’ are legal. As noted above, the sign digit ‘D’ is standard for negative numbers, while the sign digit ‘C’ is standard for non–negative numbers. The sign digit ‘F’ will be seen in data converted from Zoned Decimal by the PACK instruction.
For AP,
CP, and SP, the first operand must be a valid packed field terminated with a
valid
sign. For ZAP, the only consideration is
that the destination field be large enough.
If either
the sending field or the destination field (AP and SP) have just been created by
a PACK instruction, the sign half–byte may be represented by the sign digit ‘F’.
This is changed by the processing to ‘C’ or ‘D’ as necessary.
Some textbook hint that using ZAP to transfer a packed decimal number with ‘F’ as the sign half–byte will convert that to ‘C’. This seems reasonable.
Any packed decimal value with a sign half–byte of D (for negative) is considered to sort less than any packed decimal value with a sign half–byte of C or F (positive). This follows the standard arithmetic in which any negative number is less than any positive number.
The
number 0 is always represented as 0C (possibly with more leading
zeroes), but
is never validly represented as 0D. There is no negative zero.
Example of Packed
Decimal Instructions
The form is OP D1(L1,B1),D2(L2,B2). The object code format is as follows:
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
OP |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
Consider the assembly language statement below, which adds AMOUNT to TOTAL.
AP TOTAL,AMOUNT
Assume: 1. TOTAL is 4 bytes long, so it can hold at most 7 digits.
2. AMOUNT is 3 bytes long, so it can hold at most 5 digits.
3. The label TOTAL is at an address specified
by a displacement
of X‘50A’ from the value in register R3,
used as a base register.
4. The label AMOUNT is at an address specified
by a displacement
of X‘52C’ from the value in register R3,
used as a base register.
The object code looks like this: FA 32 35 0A 35 2C
The Disassembly of the Above Example
Consider
FA
32 35 0A 35 2C. The operation
code X‘FA’
is that for the
Add Packed (Add Decimal) instruction, which is a type SS(2). The above format applies.
The field 32 is of the form L1 L2.
The first value is X‘3’, or 3 decimal. The first operand is 4 bytes long.
The second value is X‘2’, or 2 decimal. The second operand is 3 bytes long.
The
two–byte field 35 0A indicates that register 3 is used as the base
register
for the first operand, which is at displacement X‘50A’.
The
two–byte field 35 2C indicates that register 3 is used as the base
register
for the second operand, which is at displacement X‘52C’.
It is quite common for both operands to use the same base register.
Condition Codes
Each of
the ZAP, AP, and SP instructions will set the condition codes. As a result,
one may execute conditional branches based on these operations. The branches are:
BZ Branch Zero BNZ Branch Not Zero
BM Branch if negative BNM Branch if not negative
BP Brach if positive BNP Branch if not positive
BO Branch on overflow BNO Branch if overflow has not occurred.
An overflow will occur if the receiving field is not large enough to accept the result.
My guess
is that leading zeroes are not considered in this; so that the seven–digit
packed
decimal number 0000123 can be moved to a field accepting four digit packed
numbers.
Additional Rules for ZAP, AP, and SP
These rules are as follows:
1. The
maximum length for each field is 16 bytes, allowing for a maximum of
31 digits. Either field, or both, may have an explicit
length operand with
a maximum value of 16. Remember that this operand is a byte length.
2. If
the operand 1 (destination) field is shorter than the operand 2 (source) field,
a program interrupt may
occur. The length of the first field
should be sized for
the expected result of the
operation and not just based on the length associated
with the first value. For addition, the operand 1 field should be
one digit larger
than the lengths of either of
the values to be added.
3. The
CPU extends the shorter field (presumably that associated with the second
operand) to that of the longer
field by left padding with zeroes. This
is necessary
for the results to be in
accordance with standard arithmetic.
Examples of ZAP, AP, and SP
Here are a few examples of the use of the three instructions AP, SP, and ZAP. The examples are to be viewed as independent executions of code, so that the values associated with the data labels are always the same at the beginning of each.
Suppose that we start with definitions as follows.
P0 DC P‘666’ Stored as 66 6C
P1 DC
P‘222’ Stored as 22 2C
P2 DC
P‘1234’ Stored as 01 23 4C
P3 DC P‘1234567’ Stored as 12 34 56 7C
For these examples, we assume that the data stored represent integer values, and that none has an implied decimal or “digits to the right of the decimal”.
CASE1 ZAP P3,P1 RESULTS IN P3 = 00 00 22 2C
CASE2 ZAP P2,P1 RESULTS IN P2 = 00 22 2C
CASE3 AP
P2,P1 RESULTS IN P2 = 01 45
6C.
Recall this
starts with P2 = 01 23 4C.
CASE4 SP
P2,P1 RESULTS IN P2 = 01 01
2C
CASE5 SP
P3,P1 RESULTS IN P3 = 12 34
34 5C.
In other words, the arithmetic is not blindly done left to right, but with the digits “lined up” as one would expect in standard arithmetic.
CASE6
AP P1,P1 RESULTS IN P1 = 44 4C.
CASE7 AP P0,P0 This causes an overflow.
Here we see the importance of design so that the first argument can store not just its initial value, but also the result of any reasonably contemplated arithmetic operation.
CASE8 SP P0,P0 RESULT IS 0, PRESUMABLY STORED AS 0C.
Comparing Packed
Decimal Values
The rules for the CP instruction are the same as those for the AP and SP instructions.
1. Both
operands must contain valid packed data, with maximum length of 16 bytes.
Either operand or both may
contain an explicit length indicator.
2. If
the fields are not of the same length, the CPU extends the shorter field by
padding
with left zeroes to the length
of the longer field. The comparison
remains valid.
3. All
comparisons are as in standard algebra. +0
is considered equal to –0, but
otherwise any positive value
is larger than any negative value.
The CP (Compare Packed) instruction is used to compare packed decimal values. This sets the condition codes that can be used in a conditional branch instruction, as just discussed. Is there any reason to compare and not then have a conditional branch?
In some sense, the CLC (Compare Character) instruction is similar and may be used to compare packed decimal data. However, this use is dangerous, as the CLC does not allow for many of the standards of standard algebra.
Consider the two values 123C (representing +123) and 123D (representing –123).
CP will correctly state that 123D < 123C; indeed –123 is less than +123.
CLC will state that 123D > 123C, as 12
= 12, but 3D > 3C. Remember that
these are being compared as
sequences of characters without numeric values.
Consider the two values 123C (representing +123) and 123F (also representing +123).
CP will correctly state that 123C = 123F; as 123 = 123.
CLC will state that 123F > 123C, as 12 = 12, but 3F > 3C.
Consider the two values 125C (representing +123) and 12345C (representing +12345).
CP
will work correctly, noting that 12345 > 00125. CLC will compare
character by character. As ‘5C’ > ‘34’, it will conclude that 125
> 12345
The best way to understand the results of this last comparison is to line up the two constants, and note that the comparison is left to right.
12
5C
12 34 5C
Examples of CP
Here are some examples. Consider the following data definitions.
P1 DC
P‘6’ STORED AS 6C
P2 DC P‘42’
STORED AS 04 2C
P3 DC P‘122’ STORED AS 12 2C
P4 DC P‘-56’ STORED AS 05 6D
Here are some comparisons.
CP P1,P2 P1 < P2. Compared as 00 6C to 04 2C
CP P1,P3 P1 < P3 BRANCH ON LOW (BL or BM)
CP P1,P4 P1 > P4 BRANCH ON HIGH (BH or BP)
CP P2,P3 P2 < P3
CP P2,P4 P2 > P4
CP P4,P4 P4 = P4
BRANCH ON EQUAL (BE or BZ)
Handling Decimal Precision
There is a small problem that arises due to the fact that the decimal point is not explicitly stored in the packed decimal format. Consider the following addition.
The
positive number 234.12, represented as 23
41 2C
is added to the positive number 4.5678, represented as 45 67 8C.
The sum might be represented as 69
09 0C, which
is not correct. We must keep better
track of the decimal.
It seems that the best approach is to store all values to be used in a given computation in the same format, with the same number of implied decimal digits. Assume that the above values are used in computations in which the most precise data have five decimal digits. Then we would be required to have the following.
The value 234.12 would be treated as 234.12000, and stored as 02 34 12 00 0C.
The value 4.5678 would be treated as 4.56780, and stored as 04 56 78 0C.
The sum will then be correctly stored as 02 38 68 78 0C.
MP: Multiply Packed
This is of the form OP D1(L1,B1),D2(L2,B2), which provide a 4–bit number representing the length for each of the two operands. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
X ‘FC’ |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
A typical source code example
would be MP
S1, S2. Before the
multiplication, field
S1 holds the multiplicand and field S2 holds the multiplier. After the multiplication, field
S1 holds the product. The rules for the
MP instruction are as follows.
1. Both fields must contain valid packed data.
2. The maximum length of the first operand is
16 bytes, or 31 digits. However, this
is the maximum length of
the product, not of the multiplicand.
See below.
3. The maximum length of the second operand is 8 bytes, or 15 digits.
4. Either operand or both may contain an explicit length specifier.
5. The standard rules of algebra apply: Like
signs yield a positive product and
unlike signs yield a
negative product.
6. The number of digits in the product is
usually equal to the sum of the count of
digits in the multiplicand
and the count of digits in the multiplier.
Put another way, prior to multiplication, for each byte in the multiplier, the field to hold the product must contain one byte of zero digits to the left of the significant digits that represent the multiplicand. One preferred use would be to use the ZAP instruction to move a smaller multiplicand into the product field, as shown in the illustration below.
Consider the following sequence, which might be typical of the use.
ZAP PAY, HOURS
MP PAY, RATE
PAY DC PL7‘0000000’ STANDARD IS 980.00 OR 98 00 0C
HOURS DC PL3‘400’ 40.0 HOURS PER WEEK
RATE DC PL3‘245’ PAY RATE $24.50 PER HOUR
Handling Decimal Precision
Recall
that the assembler does not track the position of the decimal point in any
packed decimal representation. That is
the responsibility of the programmer, who must write assembly language
instructions specifically to correct the product. Consider the example above. A simplistic product might be expressed as 09
80 00 0C. Is this read as
$9,800.00 (a bonus for the worker) or $980.000 (too many decimal places).
In general, the number of decimal positions in the product is equal to the sum of the number of decimal places in the multiplier and the number of decimal places in the multiplicand. If either of these is zero (or both are zero), no adjustment is required. Otherwise, the number of decimal places in the product must be adjusted.
The reason that this adjustment is required is that the number of decimal places is never tracked, but is always explicit. The only way to be able to assume the number of decimal places in a numeric representation that does not indicate that number is to have every arithmetic operation adjust the result to the correct count.
As an aside, one could write code to track the decimal position explicitly. One might store the above results as pairs of numbers, such as (1, 400) for hours, (2, 2450) for the rate, etc. However, this is not the standard approach. What is needed is a way to truncate a product to the correct number of decimal places; the SRP instruction does exactly that.
SRP: Shift and Round Packed
The SRP instruction was designed to shift packed data to the left or right, effectively dividing or multiplying by a power of ten, and then rounding the number so produced. The standard use seems to be a way to round decimal data in the usual fashion; the value 2.416 is rounded to either 2.42 or 2.4 depending on the number of decimals required. The instruction seems to support the other option, possibly called “un–rounding”, of extending 2.416 to 2.4160, etc.
While the SRP instruction can be used with the results of AP, SP, and ZAP; we discuss it here within the more natural context of MP (multiplication of packed decimal data). The reason for this choice should be obvious. The addition of two numbers with equal counts of decimal places produces a similar result; thus 2.32 + 4.56 = 6.88. On the other hand, if we multiply 2.32 by 4.56, the result is 10.5792. Depending on the application, it is common to round the result to something like 10.58, preserving the count of decimal places.
While on the subject of addition and subtraction, we do not want to overlook an obvious application of SRP. Consider the sum 2.416 + 7.32. While this is not likely to be seen in a standard assembly language program, as the programmer surely will have been careful to keep all decimal points consistent, it is a theoretical possibility. In this case, it would be necessary to use the SRP instruction to convert this to one of the two equivalent forms: either 2.416 + 7.320 = 9.736 or 2.42 + 7.32 = 9.74.
The SRP instruction is a storage–to–storage (type SS) instruction, with opcode X‘F0’. Although the SRP is a type SS instruction, it has three operands. The source code is commonly written in the form SRP PACKVAL,SHIFTCNT,ROUNDVAL.
Operand 1, here PACKVAL, denotes a packed field to shifted and possibly rounded.
Operand 2, here SHIFTCNT, indicates
the count of digits to shift. The
maximum
shift count is 31, which is the
maximum size of a packed decimal field.
Operand 3, here ROUNDVAL, contains a
single digit (0 – 9) which is to be added to
the original value before
shifting. This converts a shift
operation into a rounding.
Normally, the values are 0 for left
shifts and 5 for right shifts.
The use of the rounding value can be seen by an attempt to round the number 2.416 by shifting right one place. A pure shift would change 2.416 to 2.41, which does have one less decimal place. Use of SRP with a rounding value of 5 would first convert 2.416 to 2.421 and then shift right to obtain the value 2.42, considered as a proper rounding of 2.416.
The SRP operation sets the condition codes to indicate zero, minus, or plus.
The SRP instruction was not a part of the original S/360 architecture, but was added with the introduction of the S/370 to replace the MVO (Move with Offset) instruction. We shall not discuss the MVO instruction here; the reader is directed to reference R_02 for details.
The format of the instruction is SRP D1(L,B1),D2(B2),I3.
The object code format for the SRP instruction is represented in the figure below.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(1) |
6 |
D1(L,B1),D2(B2),I3 |
X‘F0’ |
L I3 |
B1 D1 |
D1 D1 |
B2 D2 |
D2 D2 |
L is the length indicator for the field to be shifted, denoted by PACKVAL in the example above. Remember that the length is a byte count that is one more than the value stored. Thus, the single hexadecimal digit can represent a value between 0 and 15 inclusive, to represent a field length between 1 and 16 inclusive.
I3 is the decimal digit to be added before shifting.
The two bytes B1 D1 D1 D1 represent the address of the field to be shifted (PACKVAL ), denoted in the standard base/displacement form.
The two bytes B2 D2 D2 D2 represent the shift count, using the standard base/displacement format to represent a count and not an address. The normal use would be either to use a register to hold the count, or to set the register field to 0 (indicating no base register) and use the displacement field to hold the constant value of the shift count.
There is an interesting feature of this part of the instruction that arises from the inability of the assembler to process a negative displacement. Recall that the amount shifted is given by a count in the range 0 through 31. Left shifts are denoted by positive numbers. It should be obvious that these shift counts can be represented by a five–bit binary number.
Conceptually, the right shifts used as a part of rounding are represented by negative numbers in the range from –1 through –31 inclusive. The actual format of the shift count is dictated by the need to find another way to represent these negative numbers.
The
best way to view this shift count is as a six–bit two’s–complement signed
integer.
Such a format can represent integers in the range from –32 to +31 inclusive. Some of the more common shift values would
then be stored as follows.
Shift
Description Hexadecimal Value Decimal Value
1 left 01 1
2 left 02 2
3 left 03 3
4 left 04 4
1 right 3F 63
2 right 3E 62
3 right 3D 61
4 right 3C 60
Each
of the values for right shifts can be obtained by calculating the
representation as a
six–bit two’s–complement integer.
Consider the value for “3 right”.
The value +3 as a six–bit binary number 00 0011 or X’03’.
The one’s complement of this number 11 1100 or X‘3C’.
Add one to this value to get 11 1101 or X‘3D’.
The
default format for the source code is based on decimal values and not
hexadecimal. Hexadecimal values can be
specifically indicated; e.g., X‘3D’. The easier way is to use a formula: N digits left encode with the decimal number
N.
N digits right encode with the decimal number (64 –
N).
Examples of the SRP Instruction
In each of the following examples the value in AMNT2 is being rounded by adding the value 5 and shifting right two places. The field AMNT2 is assumed to be at an address specified by the offset 0B2 from the value in base register 12 (X‘C’). The first example, showing the use of register 10 (X‘A’) to specify the shift count, uses an instruction that will be defined later.
48E030 C2 SHIFT01
LH 10,=H‘-2’ R14
GETS NEGATIVE 2
F045 C0B2 A000 SRP
AMNT2,0(10),5
F045 C0B2 003E
SHIFT02 SRP AMNT2,X‘3E’,5
F045 C0B2 003E
SHIFT03 SRP AMNT2,62,5
AMNT2 DS PL5
LENGTH IS FIVE BYTES
Disassembly of the above
In each of the above instructions (except the first, which is a load register from halfword), the opcode is X‘F0’, indicating a SRP instruction. The second byte is to be viewed as two independent hexadecimal digits. The first digit, with value 4, indicates that the length of the field to be shifted (AMNT2) is five bytes. The second digit, with value 5, is the value to be added to the field before it is shifted. The next two bytes (C0 B2) specify the address of the field to be shifted. The last two bytes specify the count for the shift.
In the first example, the count is specified by adding 0 to the value stored in a register. In the other two, the count is specified by a constant with no base register. One might use a combination of the two (as in A0 04), but this usage seems a bit strange.
DP: Divide Packed
The DP (Divide Packed) instruction divides one packed field (the dividend) by another (the divisor), producing a quotient and a remainder. The DP instruction is a storage–to–storage instruction, with opcode X‘FD’. The form is OP D1(L1,B1),D2(L2,B2), which provide a 4–bit number for the length for operand. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
X ‘FD’ |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The lengths and address calculations are just as in the other packed decimal instructions. The rules for the DP instruction are as follows.
1. Each operand must contain data in valid packed decimal format.
2. The
maximum length of the first operand (the dividend) is 16 bytes (31 digits).
The maximum length of the
second operand (the divisor) is 8 bytes (15 digits).
3. Either operand may specify an explicit length.
4. A zero divisor will cause a program interrupt.
5. DP
uses the normal rules of algebra. Like
signs in the dividend and divisor
produce a positive
quotient; unlike signs produce a negative quotient.
6. After
the division, the field that first contained the dividend now contains
the quotient and remainder,
each with a sign half–byte.
|
Before division |
Dividend |
|
|
After division |
Quotient |
Remainder |
The remainder field has a size equal to that of the divisor. Together, the quotient and remainder occupy the entire dividend field. The address of the quotient is the same as that for the dividend. The address of the remainder must be computed.
In the original operands, the dividend had length (L1 + 1) and the divisor a length (L2 + 1). In the results of the operation, the length of the remainder is also (L2 + 1), the same as that for the divisor. Thus, the length of the quotient is (L1 + 1) – (L2 + 1) = (L1 – L2), and its length code would be one less: (L1 – L2 – 1). As a result, the address of the remainder is given by A(Quotient) + (L1 – L2).
As is the case with packed decimal multiplication, the program should use the SRP instruction to adjust the number of decimal places in both the quotient and remainder. As a general rule the number of decimal places in the remainder is the same as the number in the divisor, and the number of decimal places in the quotient is the difference between the count in the dividend and that in the divisor. If the dividend does not already contain a sufficient number of decimal places, it is necessary to use the SRP instruction to generate additional positions by left shifting the dividend. In this case, the value for rounding would be 0.
This brief discussion of the DP instruction concludes our list of instructions for decimal arithmetic operations.
Conversion between EBCDIC and Packed Decimal
We have now examined a number of packed decimal arithmetic instructions. It is now time to face the problem of conversion of digits between EBCDIC format and packed decimal format. At a later time we shall address the problem of conversion between packed decimal format and two’s–complement fullword format.
When a number is read from input, it is presented as a sequence of EBCDIC characters. Arithmetic based on this input must be done in one of the standard numeric formats, unless one wants to write an extraordinary amount of support code. The results must then be converted back to EBCDIC and formatted for output. We now present a number of instructions used for this purpose.
Along the way, we shall note the inability of the standard instructions to handle signed data as input. The digits ‘0’ through ‘9’ can be processed, but the signs ‘+’ and ‘–’ cannot be. We shall comment on a number of standard tricks that older assembly language programs use to get around this problem and then write some procedures to handle the issue.
The main issue in the conversion between EBCDIC and packed decimal format is suggested by the names of the operations that can be used for those conversions PACK and UNPACK. In the EBCDIC and zoned decimal format, each decimal digit requires an 8–bit byte for its representation. In the packed decimal format, each digit requires a 4–bit hexadecimal digit. This representation introduces an amusing, but totally unimportant, ambiguity. In a value such as represented by X‘789D’, are the numeric values decimal or hexadecimal? The answer is that it does not matter, each digit requires four bits for encoding.
One of the key ideas in understanding the zoned decimal format is the division of the byte into two “half bytes” or hexadecimal digits. The most significant is called the zone part and the least significant is called the numeric part. The figure below illustrates this division.
|
Portion |
Zone |
Numeric |
||||||
|
Bit |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
There are two instructions specifically
designed to process these half–byte fields.
These are:
MVZ Move
the zone half byte, and
MVN Move
the numeric half byte.
Each of these instructions is a type SS instruction, more properly classified as character instructions than packed decimal instructions. The two are included here because their sole use seems to involve translation to and from packed decimal format.
The format of each instruction is OP D1(L,B1),D2(B2). This format reflects the fact that each of the source and destination addresses is specified by a base register (often the default base register) and a displacement. Here is the format of the object code.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(1) |
6 |
D1(L,B1),D2(B2) |
OP |
L |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The opcode for MVZ is X‘D3’, that for MVN is X‘D1’. The instruction is commonly written in source code in the form OP S1, S2. Characteristics of the two instructions include the following.
1. Each moves half bytes from the address
specified by the second operand
to an address specified by
the first operand.
2. Each may move from 1 to 256 half–bytes, as
specified by the length byte
in the object code
representation.
3. Neither move affects the contents of the second operand.
4. All of the addressing conventions used by
the character instruction MVC
may be used with either of
these instructions.
5. Each instruction moves the half–byte
associated with it and does
not affect the other half
byte.
6. The MVZ (Move Zones) moves the zone
portion of each source byte to
the zone portion of the
corresponding destination byte. It does
not
change the numeric portion
of the destination byte.
The
MVN (Move Numeric) moves the numeric portion of each source byte to
the numeric portion of the
corresponding destination byte. It does
not
change the zone portion of
the destination byte.
As we shall soon see, the MVZ instruction is of more immediate interest to this course, which nevertheless covers both as important. As always, we shall illustrate the operation of the instructions by considering two fields defined by the DC directives.
Assume that we have the following two data fields defined with initialized storage.
S1
DC C‘123’ Stored as F1 F2 F3
S2
DC X‘45 67 C8’ Stored as 45 67 C8
Execute the instruction MVN S2,
S1. This moves the numeric portion of
each byte in
S1 to the numeric portion of the corresponding byte in S2.
F1
F2 F3 becomes F1 F2 F3
45 67 C8 41 62 C3
Independently, execute the instruction MVZ S2, S1. This moves the zone portion of each byte in S1 to the zone portion of the corresponding byte in S2.
F1
F2 F3 becomes F1 F2 F3
45 67 C8 F5 F7 F8
We shall jump ahead to mention one good use of the MVZ instruction, as it applies to the process of unpacking data using the UNPK instruction. The goal of the unpacking process is to turn packed decimal data into EBCDIC format suitable for printing. However, the UNPK instruction converts from packed decimal format to zoned decimal format.
Consider the positive decimal number
1234, represented in packed decimal format as
01
23 4C. The result of an
unpack instruction will be represented in zoned decimal format as F0
F1 F2 F3 C4, which will print as the string 123D, as X‘C4’
is EBCDIC for ‘D’.
The use of the MVZ instruction is illustrated by the following. Consider the following declaration, given in hexadecimal just to make it easier to read.
S3 DC
X‘F0F1F2F3C4’ Stored as F0 F1 F2
F3 C4
The byte X‘C4’ is at location S3 + 4. The following instruction is executed.
MVZ S3+4(1),=X‘F0’
In the above instruction, the source operand is specified as a literal. Note that the second hexadecimal digit is unimportant. It is the hexadecimal digit F that occupies the zone part of the byte, and it is only that part that is moved.
The address associated with the destination is given by the relative address S3+4; it is four bytes offset from the address S3. In other words, it is the fifth byte of the five–byte string.
The (1) part of the instruction indicates that only one zone in the destination is to be changed. Here it is the zone part of the byte at the address S3+4.
The zoned decimal data stored as F0 F1 F2 F3 C4
is changed to data stored as F0
F1 F2 F3 F4
which is the proper EBCDIC for the digit string “01234”.
PACK
The pack instruction is designed to convert data in zoned decimal format, one digit per byte, to packed decimal format, with approximately two digits per byte. Due to the similarity of EBCDIC format to zoned decimal format, the instruction is commonly used to convert from EBCDIC format into packed decimal format.
The PACK instruction is a
storage–to–storage (type SS) instruction, with opcode X‘F2’.
The instruction may be written in source code as PACK PACKED,ZONED. The affect of this instruction is to take the
zoned data in the field represented by the second operand, translate it to
packed format, and place the data into the field represented by the first
operand.
The instruction is of the form PACK D1(L1,B1),D2(L2,B2), which uses the standard base/displacement addressing form for each of the two operands. Note that the length of each operand (in bytes) is also encoded. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
X ‘F2’ |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The following are the rules for PACK:
1. Operand
2 must hold data representing digits or blanks, and the rightmost byte must
hold the code for a
digit. The coding may be EBCDIC or zoned
decimal.
2. The maximum length for each operand is 16 bytes.
3. Bytes referenced by operand 2 are packed one byte at a time from right to left.
4. other
than the rightmost byte, all zones are ignored and only the numeric part of the
code is copied. For the rightmost byte, the half bytes are reversed. The zone part of
the last byte in zoned decimal
becomes the sign half byte in packed decimal.
Consider
the following two representations of the positive number 123.
As a string of EBCDIC characters, it is the three bytes F1 F2 F3.
As stored in zoned decimal format, it is the three bytes F1 F2 C3.
When
executed according to its original design, the PACK instruction operates on
data in the zoned decimal format. Its
action on this example is shown below.
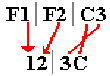
When the instruction operates on digital data in EBCDIC form, it functions identically.
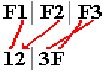
Note that the zone part of the last byte has become the sign half–byte in the packed decimal format. It is for this reason that X‘F’ is recognized as a valid sign indicator.
We now focus on conversions of
decimal data between the two formats that may
be used to represent them:
1. The EBCDIC character encoding used for input and output.
2. The packed decimal format used for decimal arithmetic.
Packing Blanks
While the PACK instruction can
handle leading blanks, a serious problem can arise if the field to be packed
contains all blanks (EBCDIC code 0x40).
Consider first an acceptable input.
Suppose that the five character string “ 2” or EBCDIC 40
40 40 40 F2
is input. What happens here? Note that the numeric part of the EBCDIC code
for the blank is the same as the numeric part of the EBCDIC code for the digit
“0”. This works, producing the packed string “00002F”,
as illustrated below.
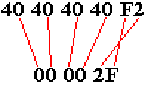
Now consider the five character input “ ” or EBCDIC 40 40 40 40 40. This will pack to the string “000004”, which lacks a valid sign, as shown below. This invalid packed input cannot be processed by any packed decimal instruction.
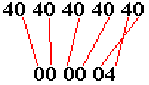
Some authors suggest checking
all input fields and replacing those that are blank
with all zeroes. This suggests a very
common meaning of blanks as equivalent to 0.
Here is the code, directly from
Abel’s textbook. The input field, RATEIN,
is
supposed to contain one to five digits, but no more than five.
CLC
RATEIN,=CL5‘ ’ Is this a field
of five blanks
BNE
D50 No, it is not
all blanks
MVC
RATEIN,=CL5‘00000’ Replace 5 blanks with 5 zeroes
D50 PACK RATEPK,RATEIN Store packed value in RATEPK
More on Input of Digits to be Formatted as Packed Data
Recall that the input of packed data is a two–step procedure.
1. Input the digits as a string of EBCDIC characters.
2. Convert the digits to packed format.
The format of the input is dictated by the appropriate data declarations.
In this example, we consider the following declaration of the form of the input, which is best viewed as an 80–column card. Here is a part of a program to read numbers, one per line.
RECORDIN DS 0CL80 80 CHARACTER CARD IMAGE
DIGITS DS
CL5 FIRST FIVE COLUMNS ARE
INPUT
FILLER DS CL75 THE OTHER 75 ARE IGNORED
Here is a properly formatted input sequence.
1 Four blanks before the “1”.
3
13
Three blanks before the “13”.
In order to see that this is the proper
format for the digits, we look at a representation that
emphasizes the column placement of the digits.
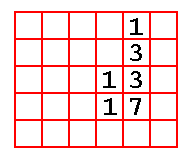
Column
4 is the tens column
Column 3 is the hundreds
column, etc.
Note that each digit is properly placed; the first line is really 00001.
One Error: Assuming
Free–Formatted Input
Here is some input from the same program. Recall that it was designed to read numbers, one per line, and to output the sum.. It did not work.
1
3
13
17
The student expected free–form
input and assumed that this would be interpreted as the sum
1 + 3 + 13 + 17 = 34. But free–form
input is an artifact of a well–written run time system, with particular
attention to the user interface.
Here is the way that the input was interpreted.
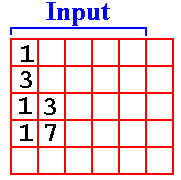
To me this looks like 10000 + 30000 + 13000 + 17000. I had expected the above input to give a sum of 70000. It did not. Here is the code loop for the processing routine.
B10DOIT MVC DATAPR,RECORDIN FILL THE PRINT AREA
PUT PRINTER,PRINT START THE PRINT
PACK PACKIN,DIGITSIN CONVERT INPUT TO DECIMAL
AP
PACKSUM,PACKIN ADD IT UP
BR
R8 RETURN FROM
SUBROUTINE
Here is the actual output. All we get is the header line and a print echo of the first line input. The header line had been printed by an earlier part of the program.
***
1
A Diagnostic
Here is the code that isolated the problem. Note the one line commented out.
B10DOIT MVC DATAPR,RECORDIN FILL THE PRINT AREA
PUT PRINTER,PRINT START THE PRINT
PACK PACKIN,DIGITSIN CONVERT INPUT TO DECIMAL
*** AP PACKSUM,PACKIN ADD IT UP
BR
R8 RETURN FROM
SUBROUTINE
The program ran to completion. Here is the output for the code fragment above.
************** TOP OF DATA
*****************************
***
1
3
13
17
THE SUM = 000000
************
BOTTOM OF DATA ****************************
The Diagnosis
Look again at the input.

The first line, as EBCDIC characters is read as follows. F1 40 40 40 40
The PACK command processes right to left. It will process any kind of data, even data that do not make sense as digits. This input will pack to X‘10004’, an invalid packed format.
With no valid sign indicator, the AP instruction fails and the program terminates.
Printing Packed Data
In order to print packed decimal data, it must be converted back to a string of EBCDIC characters. The UNPK command is a part of this conversion. It converts digital data from the packed decimal form to the zoned decimal form, which must be processed further.
The UNPK instruction is a
storage–to–storage (type SS) instruction, with opcode X‘F3’.
The instruction may be written in source code as UNPK ZONED,PACKED. The affect of this instruction is to take the
packed data in the field represented by the second operand, translate it to
zoned decimal format, and place the data into the field represented by the
first operand.
The instruction is of the form UNPK D1(L1,B1),D2(L2,B2), which uses the standard base/displacement addressing form for each of the two operands. Note that the length of each operand (in bytes) is also encoded. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
X ‘F3’ |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The following are the rules for PACK:
1. The
maximum length for each field is 16 bytes, which implies a maximum length
of 8 bytes for the field
holding the packed data. Suppose that
the packed data is
stored in 9 bytes, which would
represent 17 digits. This would unpack
to 17 bytes.
2. Bytes referenced by operand 2 are unpacked right to left, one byte at a time.
3. For
all but the rightmost byte of the packed data, each hexadecimal digit is
handled
separately, being inserted
into the numeric zone of the zoned data format.
4. The
rightmost byte of the packed data has its half bytes reversed, with its sign
half byte being moved to the
zone part of the zoned data and the left half byte
being moved to the numeric
part of the zoned data. Consider the
number 47,
which would be represented
internally as 04 7C.
When this is unpacked, we might want it to become F0 F4 F7, which would print as the three–digit string “047” or perhaps as the two–digit string “47”. However, UNPK just swaps the sign half byte to produce F0 F4 C7.
This prints as “04G”, because X‘C7’ is the EBCDIC code for the letter ‘G’.
We have to correct the zone part of the last byte. The problem occurs when handling the sign code, “C” or “D” in the Packed Decimal format. This occurs in the rightmost byte of a packed decimal value.
Printing Packed Data
(Part 2)
Here is the code that works for five digit numbers. It is written as a subroutine, that is called as BALR R8,NUMOUT.
NUMOUT
CP QTYPACK, =P‘0’ IS THE NUMBER NEGATIVE
BNM NOTNEG NO, IT IS NOT.
MVI QTYOUT+5,C‘-’ YES,
IT IS. PLACE SIGN AT QTYOUT+5
NOTNEG
UNPK QTYOUT,QTYPACK PRODUCE FORMATTED NUMBER
MVZ QTYOUT+4(1),=X’F0’ MOVE 1 BYTE TO ADDRESS QTYOUT+4
* THIS SETS THE ZONE PART CORRECTLY
BR 8 RETURN ADDRESS IN REGISTER 8
QTYPACK
DS PL3 HOLDS FIVE DIGITS IN THREE
BYTES
QTYOUT
DS 0CL6
DIGITS
DS CL5 THE FIVE DIGITS
DC CL1’ ’ THE SIGN
Again, the expression QTYOUT+4 is an address, not a value.
If QTYOUT holds C‘01234’, then QTYOUT+4 holds C ‘4’.
Here, we have accidentally introduced the standard simplistic way of representing negative numbers in the printout of an assembly language program. This is done because it is far simpler than formatting the output in the standard manner, in which the minus sign is to the left of the most significant digit in the output. The table below will illustrate the two output options as might be seen for a five–digit number.
|
Internal Value |
Standard Print Format |
Simple Print Format |
|
01
23 4C |
1234 |
01234
|
|
01
23 4D |
-1234 |
01234- |
Unpacking and Editing
Packed Decimal Data
Each of the UNPK (Unpack) and the ED (Edit) instruction will convert packed decimal data into a form suitable for printing. The ED and EDMK instructions seem to be more useful than the UNPK. In addition to producing the correct print representation of all digits, each allows for the standard output formats.
The ED instruction is a
storage–to–storage (type SS) instruction, with opcode X‘DE’.
The instruction may be written in source code as ED PRNTREP,PACKED.
The EDMK instruction is also a storage–to–storage (type SS) instruction, with opcode X‘DF’. It may be written in source code as EDMK PRNTREP,PACKED.
Each instruction is of the form OP D1(L1,B1),D2(L2,B2), which uses the standard base/displacement addressing form for each of the two operands. Note that the length of each operand (in bytes) is also encoded. The object code format is as follows.
|
Type |
Bytes |
Form |
1 |
2 |
3 |
4 |
5 |
6 |
|
SS(2) |
6 |
D1(L1,B1),D2(L2,B2) |
OP |
L1
L2 |
B1
D1 |
D1D1 |
B2
D2 |
D2D2 |
The use of the ED instruction is a two–step process.
1. Define an edit
pattern to represent the punctuation, sign, and handling of leading zeroes that is
required. Use the MVC instruction to
move this into the output
position, which is PRNTREP
in the above example.
2. Use
the ED instruction to overwrite the output position with the output string that
will
be formatted as specified by
the edit pattern. The first character in
the edit
pattern is a fill character
that is not overwritten.
The EDMK instruction is identical to the ED instruction, except that it “marks” the leftmost significant digit by returning its address as the contents of general–purpose register 1. Think of the print output being scanned left to right, towards increasing byte addresses. The most significant digit is the leftmost. We shall discuss this more thoroughly in just a bit.
Here is an example. Note that there are a number of length constraints, specifically that the length of the edit pattern match the length of the output area.
MVC
COUNPR,=X‘40202020’ Four bytes
of pattern
ED
COUNPR,COUNT
More code here
COUNPR DS
CL4
Note the sequence of events in these two lines of code.
1. The edit pattern
is moved into the output field. The
leading pair of hexadecimal
digits, 0x40, state that a
blank,‘ ’, will replace all leading zeroes.
2. The
decimal value is edited into the output field COUNPR, overwriting
the edit pattern.
The
result is printed as the four character sequence “ 1”, represented in EBCDIC
as X‘4040
40F1’.
ED: Basic Rules
The basic form of the instruction is ED S1,S2
The first operand, S1, references the leftmost byte of the edit word, which has been placed in the output area. This field will be filled with the formatted output.
The second operand, S2, references a packed field to be edited.
One key concept in the editing for output is called “significance”. In many uses, leading zeroes are not treated as significant and are replaced by the fill character.
Thus, the number represented in packed decimal format as 001C might print as “ 1” or as “001” depending on whether or not leading zeroes are required.
There are
times in which one wants one or more leading zeroes to be printed. As an
example, consider the real number 0.25, which is stored as 025C. It might best be
printed as “0.25” with at least one leading zero. This leads to the concept called
“forcing significance”, in which
leading zeroes are printed.
The Fill Character
The leftmost
hexadecimal byte in the output area before the execution of the instruction
begins represents the fill character to use when replacing non–significant
leading zeroes. Two standard values are: X‘40’ a blank ‘ ’
X‘5C’ an asterisk ‘*’ Often used in check printing.
Consider
the three digit number 172, stored internally as 172C. For now, assume that
the field from which it will be printed allows for five digits. With a fill character of X‘40’ (blank), this
would normally be printed as 172.
We can force
significance to cause either 0172 or 00172 to be
printed. For this number,
with a fill character of X‘40’, our options would be one of
the three following.
172
0172
00172
With a fill character of X‘5C’, we might have one of the three following. Note that the function of the leading “*” is to prevent other digits from being inserted at the left.
**172
*0172
00172
By itself, the leading asterisk is an inadequate security feature. However, when combined with other printing conventions (noted below), it can prevent many obvious ways of altering the amount of a check.
An amount on a properly printed check might appear as $**1,234.00.
The Edit Word:
Encountering Significance
Here are
some of the commonly used edit characters.
Note that it is more convenient
to represent these by their hexadecimal EBCDIC.
One key idea is the encounter of significance. The instruction generates digits for possible printing from left (most significant) to right (least significant). Two events cause this encounter: 1) a non–zero digit is generated, and 2) a digit is encountered that is associated with the 0x21 edit pattern. As noted above, the first character in the edit word is the fill character. The codes that are used for the digit positions are as follows:
0x20 Digit selector.
This represents a digit to be printed, unless it
happens
to be a leading non–significant zero.
In
that case, the fill character is printed.
0x21 Digit selector and significance starter. This not only represents a
digit
to be printed, but it also forces significance.
Each digit
to the
right will be printed, even if a leading zero.
Unless one is careful, ED might result in an output field that is all blanks. For printing integer values, one might seriously consider ending the edit pattern with the values 0x2120. Significance is forced after the next–to–last digit, forcing at least one digit to be printed.
As noted above, the EDMK instruction will insert the address (not the offset) of the leftmost significant digit into general–purpose register 1. This address can be decremented by 1 and then used to place a currency sign or other prefix. Please see the example below.
The Edit Word: Formatting the Output
Part of the function of the ED and EDMK commands is to allow standard formatting of the output, including decimal points and commas. Handling of negative numbers is a bit strange.
Here are the standard formatting patterns.
0x4B The decimal point. If significance has been encountered, the
decimal
point
is printed. Otherwise, the fill
character is printed.
0x6B The comma.
If significance has been encountered, the comma is
printed. Otherwise, the fill character is printed.
0x60 The minus sign, “–”. This is used in an unexpected way.
The standard for use of the minus sign arises from conventions found in commercial use. The minus sign is placed at the end of the number.
Thus the
three digit positive number 172 would be printed as 172
and the three digit negative number –172 would be printed as 172–.
The edit pattern for this output (ignoring the significance issue) would be as follows:
0x4020202060.
The fill character is a
blank. There are three digits followed
by
a
sign field, which is printed as either “–” or the fill character.
ED: An Example with
Formatting
In this example, it is desired to print a seven digit number, formatted as follows.
1. It is a fixed point number, with two digits to the right of the decimal.
2. It
has five digits to the left of the decimal and places a comma in the
standard location if
significance has been encountered.
3. It will be printed with a terminating “–” if the number is negative.
This situation is illustrated in the following graphic.
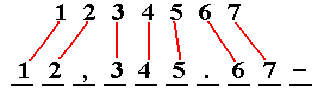
The edit pattern for this example would be as follows:
|
|
1 |
2 |
|
3 |
4 |
5 |
|
6 |
7 |
|
|
40 |
20 |
20 |
6B |
20 |
21 |
20 |
4B |
20 |
20 |
60 |
Note: The
significance forcer at digit 4 will insure that digit 5 is printed,
even if it is a zero.
EDMK: An Example
Here we
shall give an example of the use of the Edit and Mark instruction, using the
edit word that we have just discussed.
Here is the sample code:
MVC
AMTPR,EDPAT MOVE EDIT PATTERN
TO PRINT FIELD
EDMK AMTPR,AMTPAK FORMAT THE PACKED FOR PRINTING
*
* HERE REGISTER 1 CONTAINS THE BYTE
ADDRESS OF THE MOST
* SIGNIFICANT DIGIT. THE ADDRESS IS NOT LESS THAN
* (AMTPR + 1), THE ADDRESS OF “DIGIT 1”
IN THE PATTERN ABOVE.
*
SH R1,=H‘1’ DECREMENT ADDRESS BY 1
MVI 0(1),C‘$’ PLACE THE DOLLAR SIGN
EDPAT DC
X‘4020206B2021204B202060’ THE PATTERN
ABOVE
AMTPAK DC P‘12345’ THE AMOUNT TO DISPLAY
AMTPR DS CL11 THE PRINT REPRESENTATION
If the value in AMTPAK were formatted with the ED instruction, we would not be able to use the code above to place the “$” character. Here are the two outputs.
With the ED operator, the output is $ 123.45
With the EDMK instruction, the output is $123.45
ED: More on the “*” Fill Character
One option for the fill character is 0x5C, the asterisk. Why is this used? Consider the above seven–digit example, in which the number is to be viewed as a money amount. We shall use the dollar sign, “$”, in the amount.
Consider the amount $123.45. We would like to print it in this fashion, but placing the dollar sign in this way presents difficulties. Standard coding practice would have been to place the dollar sign in a column just prior to that for the digits. The format would have been as follows.
|
Column |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
$ |
Digits |
, |
Digits |
. |
Digits |
– |
||||
If the blank fill character were
chosen, this would print as $ 123.45.
Note the spaces before the first digit.
To prevent fraud, we print $***123.45
ED: A More Complete
Example
We now show the complete code for producing a printable output from the seven digit packed number considered above. We shall use “*” as a fill character. Note that the output will be eleven EBCDIC characters. Here is the code.
PRINTAMT
MVC AMNTPR,EDITWD
ED
AMTPR,AMTPACK
* The fill character is “*”. Also punctuation as follows
, .
-
EDITWD DC X‘5C20206B2021204B202060’
*
AMTPACK DS PL4
FOUR BYTES TO STORE SEVEN DIGITS.
AMTPR DS CL11
THE FORMATTED PRINT OUTPUT
ED: Another Example Using an Edit Pattern
This example is adapted from Abel’s textbook. Suppose that we have the following.
The
packed value to be printed is represented by
DC PL3‘7’ This is represented as 00 00 7C.
The edit
pattern, when placed in the output area beginning at byte address 90,
is as shown below.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
20 |
21 |
20 |
4B |
20 |
20 |
60 |
Note the structure here: 3 digits to the left of the decimal (at least one will be printed),
the decimal point, and
two digits to the right of the decimal.
This might lead one to expect something like “000.07” to be printed.
At
address 90 the contents are
0x40, assumed to be the fill character.
This
location is not altered.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
20 |
21 |
20 |
4B |
20 |
20 |
60 |
At address 91 the contents 0x20 is a digit selector. The first digit
of the
packed amount is examined. It is a 0. 00007C
ED
replaces the 0x20 with the fill character, 0x40.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
21 |
20 |
4B |
20 |
20 |
60 |
At address 92 the contents 0x21 is a digit selector and a
significance forcer
for
what follows. The second digit 00007C
of the
packed amount is of the packed amount is examined.
It is
a 0. ED replaces the 0x21 with the fill
character, 0x40.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
20 |
4B |
20 |
20 |
60 |
At address 93 the contents 0x20 is a digit selector. Significance has been
encountered. The third digit of the packed 00007C
amount
is of the packed amount is examined.
It is
a 0. ED replaces the 0x20 with 0xF0, the
code for ‘0’.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
F0 |
4B |
20 |
20 |
60 |
At address 94 the
contents 0x4B indicate that a decimal point is to be printed
if
significance has been encountered. It has
been, so the pattern
is not
changed. Had significance not been
encountered, this
would
have been replaced by the fill character.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
F0 |
4B |
20 |
20 |
60 |
At address 95 the contents 0x20 is a digit selector. Significance has been
encountered. The fourth digit of the packed 00007C
amount
is of the packed amount is examined.
It is
a 0. ED replaces the 0x20 with 0xF0, the
code for ‘0’.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
F0 |
4B |
F0 |
20 |
60 |
At address 96 the contents 0x20 is a digit selector. Significance has been
encountered. The fourth digit of the packed 00007C
amount
is of the packed amount is examined.
It is
a 7. ED replaces the 0x20 with 0xF7, the
code for ‘7’.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
F0 |
4B |
F0 |
F7 |
60 |
At address 97 the
contents 0x60 indicate to place a minus sign if the number
to be
printed is found to be negative. It is
not, so the instruction
replaces
the negative sign with the fill character.
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
40 |
40 |
40 |
F0 |
4B |
F0 |
F7 |
40 |
At this point, the process terminates. We have the EBCDIC representation of
the string to be printed. As characters,
this would be “ 0.07 ”. Note that there is a trailing space in this
printout; it occupies a column in the listing.
Note that additional code would
be required to print something like “ $ 0.07 ”.
This would involve a scan of the output of the ED instruction and placing the
dollar
sign at a place deemed appropriate.
Suppose
now that the packed value to be printed is represented by
DC PL3‘7’ This is represented as 00 00 7D.
Suppose that the edit pattern is specified as follows:
|
Address |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
Code |
5C |
20 |
21 |
20 |
4B |
20 |
20 |
60 |
The reader should verify that the print representation would be “***0.07-”.