Looping and Use of Index Registers

RX Format (Using an Index Register)

Here we shall suppose that we want register 7 to be an index register. As the second argument is at offset 4 from the first, we set R7 to have value 4.

This is a four–byte instruction of the form OP R1,D2(X2,B2).

Type	Bytes		1	2	3	4
RX	4	R1,D2(X2,B2)	OP	R₁ X₂	B₂ D₂	D₂D₂

The first byte contains the 8–bit instruction code. The second byte contains two 4–bit fields, each of which encodes a register number. The first hexadecimal digit represents the general purpose register that is the source or destination of the data. The second hexadecimal digit in the second byte represents the register used for indexed addressing. As we are assuming now that indexed addressing is being used, the value of this digit will be nonzero.

The third and fourth bytes contain an address in base/displacement format, which may be further modified by indexing.

Consider the three line sequence of instructions

L R7,=F‘4’ Register 7 gets the value 4.

L R4,FW1 Operation code is X‘58’.

A R4,FW1(R7) Operation code is X‘5A’.

The object code for the last two instructions is now.

58 40 C1 23 This address is at displacement 123
from the base address, which is in R12.

       5A 47 C1 23     R7 contains the value 4.
                       The address is at displacement 123 + 4
                       or 127 from the base address, in R12.

Address Modification: Use of Index Registers

As noted above, a type RX instruction has the form OP R1,D2(X2,B2).

This implies that the effective address is the sum of three values:

1. A displacement,

2. An address in a base register, and

3. A value in an index register.

Addresses may be modified by changing the values in any one of these three parts.
The most natural of these choices is to change the value in the index register.

We now consider an example taken from a textbook Assembler Language Programming:
the IBM System/360 and 370 (Second Edition) by George W. Struble. This example presents a number of ways to achieve the same goal. We shall comment on each of the approaches, but not claim that any one is better than the other. Before considering the entire loop, we should first examine a few lines of code as written in Mr. Struble’s style. These can be quite interesting. Struble uses R3 as the general purpose register, so we shall also.

The Structure of an Indexed Address

Consider this line of code taken from the loop example.

LOOP C R3,ARG(R10)

The instruction is a Compare Fullword, which is a type RX instruction used to compare the binary value in a register to that in a fullword at the indicated address. As we shall see, the intent of this comparison is to set up for a BE instruction. The item of real interest here is the second operand ARG(R10). How does the assembler map this to the form D2(X2,B2)?

According to Struble (page 168) “The assembler inserts the address of an
implied base register B2 for the second operand. The assembler also
calculates and inserts the appropriate displacement D2 so that D2 and B2
together address ARG. The assembler also includes X2 = 10 [hexadecimal A]
without knowledge or thought of the contents of register 10.”

If register R12 (hexadecimal C) is being used as the implied base register, and if the
label ARG is at displacement X‘234’ from the address in that register, the object
code for the above instruction is 59 3A C2 34.

Incrementing an Indexed Register

Much of this lecture will be focused on methods to change the value in the index register and so change the value of the effective address of the second argument. This set of slides, which follows Struble’s example closely, begins with an early example that he modifies to show the value of the really interesting instructions.

Consider the instruction LA R10,80(R10). What does it do?

This instruction appears to be computing an address, but is it really doing that?

The LA instruction is indeed a “load address” instruction.

Consider the value that is to be loaded into register R10.

One takes the value already in R10, adds 80 to it, and places it back into R10.

In another style, this might be written as R10 = R10 + 80.

This line of code illustrates how programmers use features of the language.

Struble’s First Loop

* PROGRAM TO SEARCH 2O NUMBERS AT ADDRESS ARG, ARG+80,

* ARG+160, ETC. FOR EQUALITY WITH A NUMBER IN REGISTER 3.

LA R10,0 SET VALUE IN R10 TO 0

LOOP C R3,ARG(R10) COMPARE TO A NUMBER

BE OUT IF FOUND, GO PROCESS IT.

LA R10,80(R10) ADD 80 TO VALUE OF INDEX REGISTER.

C R10,=F‘1600’ COMPARE TO 1600.

BNE LOOP IF NOT EQUAL, TRY AGAIN.

DO SOMETHING HERE. THE ARGUMENT IS NOT THERE

OUT DO SOMETHING HERE

This program has only one obvious flaw, but it is a big one. The loop termination code should be BL LOOP. If the value in R10 goes from 1580 to 1660 and continues incrementing, the loop with BNE will never terminate properly.

Structure Analysis of Struble’s First Loop

After correcting the obvious logic error in the above loop, it is time to discuss the structure that is implied by the program fragment. While I extend Struble’s analysis, I remain entirely consistent with it.

START Initialize the index register.

LOOP Do the comparison and branch to OUT if equal

Update the index register

Test value in index register and loop if necessary.

FALL       Write the “fall through” code here. The code
           immediately following the loop will execute only
           if the value is not found.

B MORE Jump around the code to execute if the value
has been found.

OUT        The value has been found. The value in R10
           indicates its location in the data structure
           labeled as ARG. Execute the common code next.

MORE This code is executed for any option. It
is the continuation of the processing.

Another Example from Struble

Here we have three zero–based arrays, each holding 20 fullword (32–bit) values.

We want an array sum, so that CC[K] = AA[K] + BB[K] for 0 £ K £ 19.

Here is one way to do this, again using R10 as an index register.

LA R10,0 INITIALIZE THE INDEX REGISTER

LOOP L R4,AA(R10) GET THE ELEMENT FROM ARRAY AA

A R4,BB(R10) ADD THE ELEMENT FROM ARRAY BB

ST R4,CC(R10) STORE THE ANSWER

LA R10,4(R10) INCREMENT THE INDEX VALUE BY FOUR

C R10,=F‘80’ COMPARE TO 80

BL LOOP

Here we see a very important feature: the index register holds a byte offset for an address into an array and not an “index” in the sense of a high–level language. Specifically, the address of the K^th element of array AA is at the byte address given by adding 4·K to the address of element 0 of the array.

Note also the use of LA R10,0 to initialize the register R10 to zero. This is more common in standard assembly programs than the equivalent L R10,=F‘0’.

How the VAX–11/780 Would Do This

The standard for the IBM System/360 and related mainframe computers is to use the index register as holding a byte offset from a base address. In using this feature to move through an array of particular data types, the standard is to add the size of the data item to the index register. More complex computers, such as the VAX–11/780 automatically account for
the size of the data. Here is the above code written in the VAX style, while still retaining most of the structure of a System/370 assembler language program.

LA R10,0 INITIALIZE THE INDEX REGISTER

LOOP L R4,AA(R10) GET THE ELEMENT FROM ARRAY AA

A R4,BB(R10) ADD THE ELEMENT FROM ARRAY BB

ST R4,CC(R10++) STORE THE ANSWER, INCREMENT INDEX
BY 1 FOR USE IN NEXT LOOP.

C R10,=F‘20’ COMPARE TO 20

BL LOOP

In the VAX style of programming, the address AA(R10) would be interpreted as
AA + 4·(Value in R10), because AA is an array of four–byte entries. This is a true use of an index value, as would be expected from our study of algebra. However, it is not the way that the System/370 assembler handles the addressing.

Other Options for the Loop

We now note a typical structure found in many loops. The loops tend to terminate
with code of the form seen below.

LA REG,INCR(REG) Increment the value

C REG,LIMIT Compare to a limit value

BL LOOP Branch if necessary

The only part of this structure that is not general is the assumption that the loop is
“counting up”. For a loop that counts down, we replace the last by BH LOOP.

A loop termination structure of this sort is so common that the architects of the IBM System/360 provided a number of special instructions to facilitate it.

The four instructions to be discussed here are as follows.

BXLE Branch on index lower or equal.

BXH Branch on index high.

BCT Branch on count. While this is easier to use, it is
less general than the above.

BCTR Branch on count to address in a register.

To Loop or Not To Loop

Consider the following code, which sums the contents of a table of a given size.
Here I assume that the table contents are 16–bit halfwords, beginning at address A0
and continuing at addresses A0+2, A0+4, etc. I am using 16–bit halfwords here to emphasize the fact that the value in the index register must account for the length of the operands; here each is 2 bytes long.

The first code is the general loop. It is illustrated for an array of 50 two–byte entries.

SR R6,R6 INITIALIZE INDEX REGISTER

SR R7,R7 SET THE SUM TO 0

LOOP AH R7,TAB(R6) ADD ONE ELEMENT VALUE TO THE SUM

A R6,=F‘2’ INCREMENT TO NEXT HALFWORD ADDRESS

C R6,=F‘99’ LAST VALID OFFSET IS 98

BL LOOP

On the other hand, if the table had only three entries, one might write the following code.

LH R7,TAB Load element 0 of the table

AH R7,TAB+2 Add element 1 of the table

AH R7,TAB+4 Add element 2 of the table.

Remember that the function of looping construct is to reduce the complexity of the
source code. If an unrolled loop reads more simply, then it should be used.

Branch on Index Value

The two instructions of interest here are:

BXLE Branch on index lower or equal. Op code = X‘87’.

BXH Branch on index high. Op code = X‘86’.

Each of these instructions is type RS; there are two register operands and a
reference to a memory address. The form is OP R1,R3,D2(B2).

Type	Bytes		1	2	3	4
RS	4	R1,R3,D2(B2)	OP	R₁ R₃	B₂ D₂	D₂D₂

The first byte contains the 8–bit instruction code.

The second byte contains two 4–bit fields, each of which encodes a register number. The first register is the one that will be incremented and then tested. The second hexadecimal digit in the second byte encodes a third register, which indicates an even–odd register pair containing the increment value to be used and the limit value to which the incremented value is compared.

The third and fourth byte contain a 4–bit register number and 12–bit displacement,
used to specify the memory address for the operand in storage.

Remember that this form of addressing does not use an index register.

The Even–Odd Register Pair

The form of each of the BXLE and BHX instructions is OP R1,R3,D2(B2).

The source code form of the instructions might be OP R1,R3,S2, in which the
argument S2 denotes the memory location with byte address indicated by D2(B2).

The first register , R1, is the one that will be incremented and then tested. The third register , R3, indicates the even register in an even–odd register pair. It is important to note that this value really should be an even number. While the instruction can work if R3 references an odd register, it tends to lead to the instruction showing bizarre unintended behavior.

The even register of the pair contains the increment to be applied to the register indicated
by R1. It is important to note that the increment can be a negative number.

The odd register of the pair contains the limit to which the new value in the
register indicated by R1 will be compared.

NOTATION: R3 will denote the even register of the pair, with contents C(R3).

R3+1 will denote the odd register of the even–odd pair,
with contents C(R3+1).

Discussion of BXLE: Branch on Index Less Than or Equal

This could also be called “Branch on Index Not High”.

The instruction is written as BXLE R1,R3,S2.

The object code has the form 87 R1,R3,D2(B2). The processing for this
instruction is as follows.

Step 1 Change the value in R1: R1 ¬ C(R1) + C(R3)

Step 2 Test the new value Go to S2 if C(R1) £ C(R3 + 1).

Assume that (R4) = 26, (R6) = 62, (R8) = 1, and (R9) = 40.

BXLE 4,8,S2 The even–odd register pair is R8 and R9.

The value in R4 is incremented by the value in R8.

The value in R4 is now 27. This is compared to the value
in R9. 27 £ 40, so the branch is taken.

BXLE 6,8,S2 The even–odd register pair is R8 and R9.

The value in R6 is incremented by the value in R8.

The value in R6 is now 63. This is compared to the value
in R9. 62 > 40, so the branch is not taken.

Discussion of BXH: Branch on Index High

The instruction is written as BXH R1,R3,S2.

The object code has the form 86 R1,R3,D2(B2).

Step 1 Change the value in R1 R1 ¬ C(R1) + C(R3)

Step 2 Test the new value Go to S2 if C(R1) > C(R3 + 1).

Assume that (R4) = 4, (R6) = 12, (R8) = –4, and (R9) = 0.

BXH 4,8,S2 The even–odd register pair is R8 and R9.

The value in R4 is incremented by the value in R8.

The value in R4 is now 0. This is compared to the value
in R9. 0 £ 0, so the branch is not taken.

BXH 6,8,S2 The even–odd register pair is R8 and R9.

The value in R6 is incremented by the value in R8.

The value in R6 is now 8. This is compared to the value
in R9. 8 > 0, so the branch is taken.

A New Version of the Array Addition

Again we have three zero–based arrays, each holding 20 fullword (32–bit) values.

We want an array sum, so that CC[K] = AA[K] + BB[K] for 0 £ K £ 19.

Here is one way to do this, again using R10 as an index register.

This time, we use BXLE with R8 as the increment register and R9 as the limit register.

LA R10,0 INITIALIZE THE INDEX REGISTER

LA R8,4 INCREMENT BY 4 BYTES FOR FULLWORD

LA R9,76 OFFSET OF 19TH ELEMENT

LOOP L R4,AA(R10) GET THE ELEMENT FROM ARRAY AA

A R4,BB(R10) ADD THE ELEMENT FROM ARRAY BB

ST R4,CC(R10) STORE THE ANSWER

BXLE R10,R8,LOOP INCREMENT R10 BY 4, COMPARE TO 76

When the 19^th element is processed R10 will have the value 76 (the proper byte offset).
After the 19^th element is processed, R10 will be incremented to have the value 80,
and the branch will not be taken.

Polynomial Evaluation Using Horner’s Rule

Horner’s rule is a standard method for evaluating a polynomial for a given argument.

Let P(X) = A_N·X^N + A_N–1·X^N–1 + …. + A₂·X² + A₁·X + A₀.

Let X₀ be a specific value of the argument. Evaluate P(X₀).

For example, let P(X) = 2·X³ + 5·X² – 7·X + 10, with X₀ = 2.

Then P(2) = 2·8 + 5·4 – 7·2 + 10 = 16 + 20 – 14 + 10 = 32.

Examination of the specific polynomial will show the motivation for Horner’s rule.

P(X) = 2·X³ + 5·X² – 7·X + 10

=(2·X² + 5·X – 7)·X + 10

=( [2·X + 5]·X – 7)·X + 10

So P(2) = ( [2·2 + 5]·2 – 7)·2 + 10 = ( [4 + 5]·2 – 7)·2 + 10

= ( [9]·2 – 7)·2 + 10 = (18 – 7)·2 + 10

= (11)·2 + 10 = 22 + 10 = 32

A Standard Algorithm for Horner’s Rule

The basic loop is quite simple. In a higher–level language, we would something
like the following, which has no error checking code.

P = A[N]

For J = (N – 1) Down To 0 Do

P = P·X + A[J] ;

Consider again the polynomial P(X) = 2·X³ + 5·X² – 7·X + 10, with X₀ = 2.

In a notation appropriate for coding we have the following.
A[3] = 2, A[2] = 5, A[1] = – 7, A[0] = 10, and X0 = 2.

Let’s use the loop above to evaluate the polynomial. N = 3.

Start with P = A[3] = 2.

J = 2 P = P·2 + A[2] = 2·2 + 5 = 9

J = 1 P = P·2 + A[1] = 9·2 – 7 = 11

J = 0 P = P·2 + A[0] = 11·2 + 10 = 32.

NOTE: This is entirely different from finding the root of a polynomial.

A Sketch of Our Algorithm for Horner’s Rule

Our version of the assembler does not support explicit loops, so we write the equivalent
code. In this, I shall use register names as “variables”, so R3 will contain a value.

Algorithm Horner

On entry: R3 contains N, the degree of the polynomial
R4 contains X, the value for evaluation.

Set R8 = 0 This will be the answer.

If R3 < 0 Go to END No negative degrees

LOOP R8 = R8·R4 + A0[R3]

R3 = R3 – 1

If R3 ³ 0 Go to LOOP

END

This implementation will assume halfword arithmetic; all values are 16–bit integers.

More commonly, one would use floating–point arithmetic. Since my goal here is
to illustrate the loop structure, I stick to the simpler arithmetic of halfwords.

More Notes on Our Implementation

The array will be laid out as a sequence of halfword (two byte) entries in memory.

The base address of the array will be denoted by the label A0.

There are (N + 1) entries, from A₀ through A_N, found at byte addresses A0, …, A0+2·N.
Here is an example for a 5^th degree polynomial, with address offsets in decimal.

Address	A0	A0+2	A0+4	A0+6	A0+8	A0+10
Entry	A₀	A₁	A₂	A₃	A₄	A₅

Each halfword in the array will be referenced as A0(R3), where R3 contains the byte
offset of the item. The value in R3 will be set to 2·N and counted back to 0.

The increment value for R3 is –2 (X‘FFFFFFFE’), so that the register is actually
decremented by 2. Its values are the byte offsets: 2·N, 2·N – 2, …, 4, 2, 0.

As I want to use the BXH instruction for this illustration, and want to allow for R3 = 0,
I shall set the limit for the comparison to –1, though –2 would do as well. At the last execution of the loop, R3 will be decremented from R3 = 0 to R3 = – 2. The branch will not be taken.

Horner’s Rule Polynomial Evaluation with BXH

* ALGORITHM HORNER

* ON ENTRY: R3 CONTAINS THE DEGREE OF THE POLYNOMIAL

* R4 CONTAINS THE VALUE OF X FOR P(X)

* PROCESS: R6 AND R7 WILL BE USED FOR THE BXH

* ON EXIT: R9 CONTAINS THE VALUE OF P(X).

SR R9,R9 SET R9 TO ZERO

AR R3,R3 DOUBLE R3 TO MAKE BYTE COUNT.

LH R6,=H‘-2’ LOAD INCREMENT OF -2

LH R7,=H‘-1’ LOAD LIMIT FOR TESTING

LOOP MR R8,R4 PRODUCT IN REGISTER PAIR R8,R9
FOR HALFWORDS, R8 IS NOT USED

AH R9,A0(R3) ADD THE COEFFICIENT

BXH R3,R6,LOOP LOOP IF C(R3) > -1.

For this example, I assume 16–bit integers (halfwords) for both the value of X and
the values of all coefficients of the polynomial.

Given this, the sign bit in R9 will be correct after the multiplication and R8 is not used.

Branch on Count

The two instructions of interest now are:

BCT The branch on count instruction is a type RX instruction, with op code X‘46’.

BCTR The branch on count (register) instruction is a type RR instruction.
This has op code X‘06’. The register holds the branch address.

The forms of the instructions are: BCT R1,S2

BCTR R1,R2.

Each of these instructions decrement the count in the R1 register by 1.

The action of each of these instructions is described formally as follows.

BCT: R1 ¬ C(R1) – 1

Branch to S2 if C(R1) ¹ 0.

BCTR: R1 ¬ C(R1) – 1

Branch to C(R2) if C(R1) ¹ 0 and R2 ¹ 0.

Note that BCTR R1,0 will decrement R1 by 1, but not branch for any value in R1.

Scanning Text for Input/Output

Remember that input should be viewed as a card image of 80 columns and that output
should be viewed as a line–printer line of 132 columns, with leading print control.

Consider a field of N characters found beginning in column M.

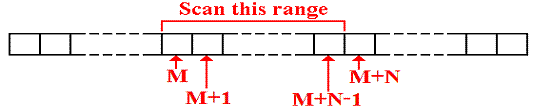
Suppose that the leftmost byte in this array is associated with the label BASE.

The leftmost byte in the range of interest will be denoted by the label BASE+M.

Elements in this range will be referenced using an index register as BASE+M(Reg).

For example, suppose that the field of interest contains 12 characters and
begins with column 20. It then goes between columns 20 and 31, inclusive.

Using R3 as an index, we reference this as BASE+20(R3), with 0 £ (R3) < 20.

Scanning left to right will use BXLE and scanning right to left will use BXH.

Arrays and Tables

We now begin our discussion of arrays and tables with yet another presentation of the various ways in which addresses can be computed. The two primary modes are indexed addressing and explicit use of base registers. We shall investigate how these two modes can be combined. The primary issue being addressed once again is the fact that some address specifications require detailed inspection in order to understand.

The reason for this endless repetition is your author’s desire to have each chapter contain a complete description of the topic, without too much direct reference to other chapters.

All classes of instructions, except type RR, can use the explicit base register format of address specification. These notes focus on four types that are of interest to our discussion of tables and arrays: type RS, type RX, and the two variants of type SS. Of these, only the type RX instructions can directly use indexed addressing. The other 3 types use a non–negative displacement from an address stored in a base register; this can be viewed as being equivalent to indexed addressing (if one is of a mind to do so).

Type RS Instruction Format

This is a four–byte instruction of the form OP R1,R3,D2(B2).

Type	Bytes	Operands	1	2	3	4
RS	4	R1,R3,D2(B2)	OP	R₁ R₃	B₂ D₂	D₂D₂

The first byte contains the 8–bit instruction code.

The second byte contains two 4–bit fields, each of which encodes a register number. Some RS format instructions use only one register, here R3 is set to 0. This instruction format follows the IBM architecture standard that “0” is taken as no register, rather than register R0.

The third and fourth byte contain a 4–bit register number and 12–bit displacement, used to specify the memory address for the operand in storage. Recall that each label in the assembly language program references an address.

Any address in the format of base register and displacement will appear in the form.

B D₁

D₂ D₃

B is the hexadecimal digit representing the base register.

The three hexadecimal digits D₁ D₂ D₃ form the 12–bit displacement, which is to be interpreted as a non–negative integer in the range from 0 through 4095, inclusive.

As an example of the type, we consider the BXH instruction with opcode X‘86’.

A standard use of the instruction would be as follows.

BXH R6,R8,L10LOOP

It is important to remember that the above could be written in source code in this form.

LA R4,L10LOOP ADDRESS OF LABEL L10LOOP INTO R4
BXH R6,R8,0(4) BRANCH TARGET ADDRESS IN R4.

One might have an instruction of the following form as well.

BXH R6,R8,12(4) BRANCH TARGET ADDRESS IS DISPLACED
12 (X‘C’) FROM ADDRESS IN R4.

RX (Register–Indexed Storage) Format

This is a four–byte instruction of the form OP R1,D2(X2,B2).

Type	Bytes	Operands	1	2	3	4
RX	4	R1,D2(X2,B2)	OP	R₁ X₂	B₂ D₂	D₂D₂

The first byte contains the 8–bit instruction code.

The second byte contains two 4–bit fields, each of which encodes a register number. The first hexadecimal digit, denoted R₁, identifies the register to be used as either the source or destination for the data. The second hexadecimal digit, denoted X₂, identifies the register to be used as the index. If the value is 0, indexed addressing is not used.

The third and fourth bytes contain a standard address in base/displacement format.

As an examples of this type, we consider the two following instructions:
L Load Fullword Opcode is X‘58’
A Add Fullword Opcode is X‘5A’

We consider a number of examples based on the following data declarations. Note that the data are defined in consecutive fullwords in memory, so that fixed offset addressing can be employed. Each fullword has a length of four bytes.

DAT1 DC F‘1111’

DAT2 DC F‘2222’ AT ADDRESS (DAT1 + 4)

DAT3 DC F‘3333’ AT ADDRESS (DAT2 + 4) OR (DAT1 + 8)

A standard code block might appear as follows.

L R5,DAT1

A R5,DAT2

A R5,DAT3 NOW HAVE THE SUM.

One variant of this code might be the following. See page 92 of R_17.

LA R3,DAT1 GET ADDRESS INTO R3

L R5,0(,3) LOAD DAT1 INTO R5
A R5,4(,3) ADD DAT2, AT ADDRESS DAT1+4.

A R5,8(,3) ADD DAT3, AT ADDRESS DAT1+8.

Note the leading comma in the construct (,3), which is of the form (Index, Base). This indicates that no index register is being used, but that R3 is being used as a base register.

Here is another variant of the above code.

LA R3,DAT1 GET ADDRESS INTO R3

LA R8,4 VALUE 4 INTO REGISTER 8

LA R9,8 VALUE 8 INTO REGISTER 9

L R5,0(,3) LOAD DAT1 INTO R5
A R5,0(8,3) ADD DAT2, AT ADDRESS DAT1+4.

A R5,0(9,3) ADD DAT3, AT ADDRESS DAT1+8.

Explicit Base Addressing for Character Instructions

We now discuss a number of ways in which the operand addresses for character instructions may be presented in the source code. One should note that each of these source code representations will give rise to object code that appears almost identical. These examples are taken from Peter Abel [R_02, pages 271 – 273].

Assume that general–purpose register 4 is being used as the base register, as assigned at
the beginning of the CSECT. Assume also that the following statements hold.

1. General purpose register 4 contains the value X‘8002’.

      2.   The label PRINT represents an address represented in base/offset form as 401A; that
            is it is at offset X‘01A’ from the value stored in the base register, which is R4.
            The address then is X‘8002’ + X‘01A’ = X‘801C’.

      3.   Given that the decimal number 60 is represented in hexadecimal as X‘3C’,
            the address PRINT+60 must then be at offset X‘01A’ + X‘3C’ = X‘56’ from
            the address in the base register. X‘A’ + X‘C’, in decimal, is 10 + 12 = 16 + 6.

            Note that this gives the address of PRINT+60 as X‘8002’ + X‘056’ = X‘8058’,
            which is the same as X‘801C’ + X‘03C’. The sum X‘C’ + X‘C’, in decimal, is
            represented as 12 + 12 = 24 = 16 + 8.

      4.   The label ASTERS is associated with an offset of X‘09F’ from the value in the
            base register; thus it is located at address X‘80A1’. This label references a storage
            of two asterisks. As a decimal value, the offset is 159.

      5.   That only two characters are to be moved by the MVC instruction examples to be
            discussed. Since the length of the move destination is greater than 2, and since the
            length of the destination is the default for the number of characters to be moved, this
            implies that the number of characters to be moved must be stated explicitly.

The first example to be considered has the simplest appearance. It is as follows:

MVC PRINT+60(2),ASTERS

The operands here are of the form Destination(Length),Source.
            The destination is the address PRINT+60. The length (number of characters
            to move) is 2. This will be encoded in the length byte as X‘01’, as the length
            byte stores one less than the length. The source is the address ASTERS.

As the MVC instruction is encoded with opcode X‘D2’, the object code here is as follows:

Type	Bytes	Operands	1	2	3	4	5	6
SS(1)	6	D1(L,B1),D2(B2)	OP	L	B₁ D₁	D₁D₁	B₂ D₂	D₂D₂
			D2	01	40	56	40	9F

The next few examples are given to remind the reader of other ways to encode
what is essentially the same instruction.

These examples are based on the true nature of the source code for a MVC instruction, which is MVC D1(L,B1),D2(B2). In this format, we have the following.

1. The destination address is given by displacement D1 from the address stored in
the base register indicated by B1.

2. The number of characters to move is denoted by L.

3. The source address is given by displacement D2 from the address stored in
the base register indicated by B2.

The second example uses an explicit base and displacement representation of the destination address, with general–purpose register 8 serving as the explicit base register.

LA R8,PRINT+60 GET ADDRESS PRINT+60 INTO R8

MVC 0(2,8),ASTERS MOVE THE CHARACTERS

Note the structure in the destination part of the source code, which is 0(2,8).

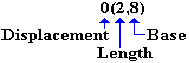
The displacement is 0 from the address X‘8058’, which is stored in R8. The object code is:

Type	Bytes	Operands	1	2	3	4	5	6
SS(1)	6	D1(L,B1),D2(B2)	OP	L	B₁ D₁	D₁D₁	B₂ D₂	D₂D₂
			D2	01	80	00	40	9F

The instruction could have been written as MVC 0(2,8),159(4), as the label
ASTERS is found at offset 159 (decimal) from the address in register 4.

The third example uses an explicit base and displacement representation of the destination address, with general–purpose register 8 serving as the explicit base register.

LA R8,PRINT GET ADDRESS PRINT INTO R8

MVC 60(2,8),ASTERS SPECIFY A DISPLACEMENT

Note the structure in the destination part of the source code, which is 60(2,8).

The displacement is 60 from the address X‘801C’, stored in R8. The object code is:

Type	Bytes	Operands	1	2	3	4	5	6
SS(1)	6	D1(L,B1),D2(B2)	OP	L	B₁ D₁	D₁D₁	B₂ D₂	D₂D₂
			D2	01	80	3C	40	9F

The instruction could have been written as MVC 60(2,8),159(4), as the label
ASTERS is found at offset 159 (decimal) from the address in register 4.

Explicit Base Addressing for Packed Decimal Instructions

Consider the following source code, taken from Abel. This is based on a conversion of a weight expressed in kilograms to its equivalent in pounds; assuming 1kg. = 2.2 lb. Physics students will please ignore the fact that the kilogram measures mass and not weight.

ZAP POUNDS,KGS MOVE KGS TO POUNDS

MP POUNDS,FACTOR MULTIPLY BY THE FACTOR
SRP POUNDS,63,5 ROUND TO ONE DECIMAL PLACE

KGS DC PL3‘12.53’ LENGTH 3 BYTES

FACTOR DC PL2‘2.2’ LENGTH 2 BYTES, AT ADDRESSS KGS+3

POUNDS DS PL5 LENGTH 5 BYTES, AT ADDRESS KGS+5

The value produced is 12.53·2.2 = 27.566, which is rounded to 27.57.

The instructions we want to examine in some detail are the MP and ZAP, each of which
is a type SS instruction with source code format OP D1(L1,B1),D2(L2,B2). Each of the two operands in these instructions has a length specifier.

In the first example of the use of explicit base registers, we assign a base register to
represent the address of each of the arguments. The above code becomes the following:

LA R6,KGS ADDRESS OF LABEL KGS

LA R7,FACTOR ADDRESS

LA R8,POUNDS

ZAP 0(5,8),0(3,6)

MP 0(5,8),0(2,7)

SRP 0(5,8),63,5

Each of the arguments in the MP and ZAP have the following form:

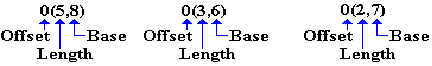
Recall the definitions of the three labels, seen just above. We analyze the instructions.

ZAP 0(5,8),0(3,6) Destination is at offset 0 from the address
stored in R8. The destination has length 5 bytes.

Source is at offset 0 from the address stored
in R6. The source has length 3 bytes.

MP 0(5,8),0(2,7) Destination is at offset 0 from the address
stored in R8. The destination has length 5 bytes.

Source is at offset 0 from the address stored
in R7. The source has length 2 bytes.

But recall the order in which the labels are declared. The implicit assumption that the labels are in consecutive memory locations will here be made explicit.

KGS DC PL3‘12.53’ LENGTH 3 BYTES

FACTOR DC PL2‘2.2’ LENGTH 2 BYTES, AT ADDRESSS KGS+3

POUNDS DS PL5 LENGTH 5 BYTES, AT ADDRESS KGS+5

In this version of the code, we use the label KGS as the base address and reference all other addresses by displacement from that one. Here is the code.

LA R6,KGS ADDRESS OF LABEL KGS

ZAP 5(5,6),0(3,6)

MP 5(5,6),3(2,6)

SRP 5(5,6),63,5

Each of the arguments in the MP and ZAP have the following form:

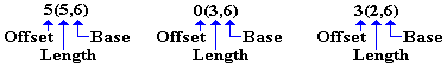
Recall the definitions of the three labels, seen just above. We analyze the instructions.

ZAP 5(5,6),0(3,6) Destination is at offset 5 from the address
stored in R6. The destination has length 5 bytes.

Source is at offset 0 from the address stored
in R6. The source has length 3 bytes.

MP 5(5,6),3(2,6) Destination is at offset 5 from the address
stored in R6. The destination has length 5 bytes.

Source is at offset 3 from the address stored
in R6. The source has length 2 bytes.

In other words, the base/displacement 6000 refers to a displacement of 0 from the address stored in register 6, which is being used as an explicit base register for this operation. As
the address in R6 is that of KGS, this value represents the address KGS. This is the object code address generated in response to the source code fragment 0(3,6).

The base/displacement 6003 refers to a displacement of 3 from the address stored in register 6, which is being used as an explicit base register for this operation. As the address in R6 is that of KGS, this value represents the address KGS+3, which is the address FACTOR. This is the object code address generated in response to the source code fragment 3(2,6).

The base/displacement 6005 refers to a displacement of 5 from the address stored in register 6, which is being used as an explicit base register for this operation. As the address in R6 is that of KGS, this value represents the address KGS+5, which is the address POUNDS. This is the object code address generated in response to the source code fragment 5(5,6).

It is worth notice, even at this point, that the use of a single register as the base from which to reference a block of data declarations is quite suggestive of what is done with a DSECT, also called a “Dummy Section”.

Tables and Arrays

In an early way of speaking, before the term “data structures” became common, structured data in a program might be organized in a table. According to [R_02, p 278] data tables “contain a set of related data arranged so that each item can be referenced according to its location in the table. … A static table contains defined data, such as income tax steps….
A dynamic table consists of a series of adjacent blank or zero fields defined to store or accumulate related data.”

We would call these structures “arrays”, with the static table corresponding to an array of constant values and the dynamic table corresponding to a plain array. The main difference in the table structure, other than the older terminology, is that the values stored in tables can be composite values. One might consider these tables as equivalent to an array of records or an array of structures. In each of tables and arrays, the elements are addressed using an offset from the base address of the table or array.

Let’s now learn some of the older IBM terminology for tables.

Sample Table

Consider the following table, adapted from the [R_02, page 279].

* 123456789

MONTAB DC C‘01’,‘JANUARY ’

DC C‘02’,‘FEBRUARY ’

...

DC C‘09’,‘SEPTEMBER’

DC C‘10’,‘OCTOBER ’

DC C‘11’,‘NOVEMBER ’

DC C‘12’,‘DECEMBER ’

In the terminology of the book, the first string (representing the month number) is called the table argument. The month name is called the table function.

The table is to be searched using a value that may match one of the table arguments.
This value is called the search argument.

While one might think of this in terms of a database table, there is no requirement (other than good coding practice) that the table arguments be unique. There are no keys to this table.

Note that the following table is exactly equivalent.

* 12345678901

MONTAB DC C‘01JANUARY ’

DC C‘02FEBRUARY ’

...

DC C‘09SEPTEMBER’

DC C‘10OCTOBER ’

DC C‘11NOVEMBER ’

DC C‘12DECEMBER ’

Note also that every table entry has exactly the same length (11 characters).
This is required by the table search algorithm.

Searching the Table by “Key Value”

Here is a fragment of code, written in a better style, that searches the above table.
The search argument, MONIN, is defined as two digits.

USING *,4,5

LA 8,MONTAB Address of table in R8

L 9,=H’12’ Number of entries in table

C10LOOP CLC MONIN,0(8) Compare to table argument

BE C30EQUAL Have a match

BL C20NOTEQ Table is ordered; no hit.

AH 8,=H‘11’ Move to next row

BCT 9,C10LOOP Decrement counter, branch if > 0

C20NOTEQ Do something

BR C40DONE

C30EQUAL Do something else.

C40DONE Common code here.

Note that the search argument is being compared to the two characters at the addresses
MONTAB, MONTAB + 11, MONTAB + 22, …, etc. One of the interesting features of this loop is the address of the second argument in the instruction at address C10LOOP. The address is specified by 0(8), which is a displacement of 0 from the address in R8.

Note that this is a counted loop. It will search no more than twelve table entries. This is a bit unusual in that the index used to count the loop is not directly used to address the table; that is done by explicitly adding 11 to the address in R8 for each loop.

Again, this looping construct is allowed due only to the regular nature of the table;
all entries stored have the same length. In this case, the length is 11 bytes.

Ordered and Unordered Tables

Quite often, a table of the above form will be ordered by the table argument. The most common order is that the table entries are sorted in increasing order by table entry. Here is the approach to searching such a table. There are three possibilities for the comparison.

1. The search argument is equal. The table function has been found and
can be used.

2. The search argument is high. Continue the search unless this is the
last entry in the table.

3. The search argument is low. Stop the search and take action appropriate
to the type of table. If it is a table with steps, return with the step number.

For unordered tables, the basic comparisons are restricted to Equal or Not Equal.

As we know, ordered tables can be searched using binary search. This very efficient search technique is discussed in the textbook.

Linked Lists

It is possible to use the table structure to implement a linked list. Every entry in the table contains an additional field specifying the offset in the table of the next item in the list.

Here is a table structured in the form of a linked list that is sorted by increasing part
number. The next offset is found at the end of the list.

Offset Part No. Price Next Offset

0000 0103 12.50 0036

0012 1720 08.95 0024

0024 1827 03.75 0000

0036 0120 13.80 0048

0048 0205 25.00 0012

There are many improvements in this structure that would lead to more flexibility and an improved set of algorithms to access the list. We may consider some of these later; by developing an insert and delete method, as well as a more modern create method.

Direct Table Addressing

Consider a table in which the table arguments are sequential and consecutive. One good example would be the table of months, already discussed. In this type of table, the table argument is implied by the entry position in the table. This could be written as:

MONTAB DC C‘JANUARY ’

DC C‘FEBRUARY ’

...

DC C‘SEPTEMBER’

DC C‘OCTOBER ’

DC C‘NOVEMBER ’

DC C‘DECEMBER ’

Entry K in the table is at offset (K – 1)·9

Let us define the following terms.

A(F) is the address of the required function (table entry).

A(T) is the address of the table.

SA is the numeric value of the search argument
with range 1 through table_length.

L is the length (in bytes) of each function (table entry).
All table entries have the same length.

The equation of interest is

A(F) = A(T) + (SA – 1)·L

This is just the access formula for describing a singly dimensioned array in memory. Note that this formula assumes that the base index has value 1, so that an array declared as A[10] would have SA as an index value in the range 1 through 10 inclusive.

For an array that has its first index as 0, the equation would be A(F) = A(T) + SA·L .