Integers are converted from halfword (16 bit or 2 bytes) to fullword (32 bits or 4 bytes) format by sign extension. This process insures that the sign of the number is preserved.
+165 in 16
bits is 0000 0000 1010 0101
+165 in 32 bits is 0000 0000 0000 0000 0000 0000 1010 0101
–165 in 16
bits is 1111 1111 0101 1011
–165 in 32 bits is 1111 1111 1111 1111 1111 1111 0101 1011
In each
case, it is the leftmost bit in the 16–bit (halfword) representation that is
copied to the leftmost 16 bits added when moving to the 32–bit (fullword)
format.
The
assumption is that the binary number to be considered will be stored in a
general–purpose register, such as R7.
The register might be loaded by an instruction such as one of the two
following.
L
R7,FW1 Load R7 from a fullword
in memory
LH R7,HW1 Load R7 from a halfword in memory,
and sign extend to a fullword format.
The goal of the input program
will be to convert from the EBCDIC digit representation,
which is really just a sequence of character codes, into a binary number in a
register.
EBCDIC Representation of Digits
When digits are read in from an input device, they are treated as character data that only incidentally have numeric value. These must be converted to a numeric format.
The EBCDIC codes of interest in the representation of integer data are the following.
Code Digit Code Digit
X‘F0’ 0 X‘F5’ 5
X‘F1’ 1 X‘F6’ 6
X‘F2’ 2 X‘F7’ 7
X‘F3’ 3 X‘F8’ 8
X‘F4’ 4 X‘F9’ 9
The two other codes of interest are X‘40’ for the space and X‘60’ for the minus sign.
Print Representation of Integers
It goes without saying that the print representation of any integer will involve the use of EBCDIC characters, especially the ones listed just above. What must be considered is how to present negative integers. Consider the negative integer 165 to be printed as four digits.
The standard algebraic way to do this is -165.
A less used way is to print it in this form - 165.
A way commonly seen in mainframe programs is as follows 165-.
The last way, though appearing strange, is quite easy to program. For this reason, many assembler language programs will use the “postfix minus sign” for negative numbers. The second way involves a bit more code to produce, and the first way considerably more code. It is this algebraically correct representation that is our goal in this chapter.
NUMIN: A Program to
Input Binary Integers
Numeric data are input into a computer in a three step process.
1. The data are read in as a sequence of characters.
For the IBM System/360, the characters are encoded as EBCDIC.
2. The data are converted to the proper form for numeric use.
3. The data are
stored, either in memory or general–purpose registers,
for use in computations.
We shall focus on the input of integer data to be stored in one of the general–purpose registers. As an arbitrary constraint, we shall limit the numbers to 9 digits, though the numbers are allowed to be smaller.
Note that any possible nine–digit integer can be stored as a
32–bit fullword. While it is the case
that some ten–digit numbers can be stored as a fullword, this does not hold for
all such numbers; for example:
The ten digit number 2, 100,
000, 000 can be converted to fullword format.
The ten digit number 2, 200,
000, 000 cannot be converted to fullword format.
It is for this reason that our code will focus on numbers with a maximum of nine digits, represented by ten characters, allowing for an optional sign character.
NUMIN: The Scenario
Remember
that input should be viewed as a card image of 80 columns. Consider a field of
N characters found beginning in column M.
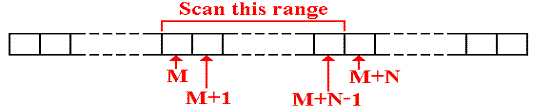
Suppose that the leftmost byte in this array is associated with the label CARDIN. The leftmost byte in the range of interest will be denoted by the label CARDIN+M. Elements in this range will be referenced using an index register as CARDIN+M(Reg), where the number in parentheses represents the index register to be used.
Our specific example will assume the following:
1. The
character field to hold the integer occupies ten columns on the card,
beginning in column 20 and
running through column 29.
2. The number is right justified. If negative, the number has a leading minus sign.
3 An entirely blank field is accepted as representing the number zero.
NUMIN: The Standard
Approach
We begin this set of notes by recalling a more standard approach to conversion from a sequence of EBCDIC characters to a binary number in a register. This sample code will assume that all numbers are non–negative.
Here are some data declarations that are used in the code. Note that the data declaration seems to call for ten digits. Here the assumption will be that the input has at least one leading space and at most nine numeric digits with no sign.
* THE CHARACTERS FOR
INPUT ARE FOUND BEGINNING
* AT CARDIN+20 THROUGH
CARDIN+29. NO MINUS SIGN.
DIGITSIN DS CL10 TEN
BYTES TO HOLD 10 CHARACTERS
PACKEDIN DS PL6 SIX
BYTES HOLD 11 DIGITS
PACKDBL DS D DOUBLE WORD TO HOLD PACKED
Here is the code that uses the above data structures.
MVC DIGITSIN(10),CARDIN+20 GET 10 CHARACTERS
PACK
PACKEDIN,DIGITSIN CONVERT TO PACKED
ZAP PACKDBL,PACKEDIN FORMAT FOR CVB
CVB R7,PACKDBL BINARY INTO R7.
NUMIN: The Strategy
The figure below shows the part of the 80–column card image that contains the digits to be interpreted. We now discuss the strategy to be followed in our direct conversion routine.

The algorithm works as follows:
1. It initializes an output register to 0. Arbitrarily, I choose R7.
2. It scans left to right, looking for a nonblank character.
Assuming that a nonblank character is found in this field, it does the following.
3. If the
character is a minus sign, set a flag that the number is negative
and continue the scan.
4. If the number is a digit, process it. If not a digit or “–”, ignore it.
One problem of this code is typical of most sample code. In an attempt to focus on one point, the code ignores all error processing. Just be aware of the fact.
NUMIN: EXAMPLE
Consider processing the number represented by the digit string “9413”. We shall illustrate the process used by our conversion routine.
In this example, let N be the value of the number,
D be the digit read in, and
V be the numeric value of that digit.
Start with N = 0.
Read in D = “9”. Convert to V = 9. N = N·10 + V = 0·10 + 9 = 9
Read in D = “4”. Convert to V = 4. N = N·10 + V = 9·10 + 4 = 94
Read in D = “1”. Convert to V = 1. N = N·10 + V = 94·10 + 1 = 941
Read in D = “3”. Convert to V = 3. N = N·10 + V = 941·10 + 3 = 9413
The integer value of this string is 9413.
Review of the Instructions: LCR and IC
The code below will use two instructions that should be reviewed at this point. These are LCR (Load Complement Register) and IC (Insert Character).
Load Complement Register: LCR R1,R2
This loads register R1 with the negative (two’s–complement) of the value in register R2. This is a convenient way to change the sign of the integer in a register; set the value in the register equal to the negative of the value now there.
Insert Character: IC
R8,CARDIN+20(R3) GET THE DIGIT
This inserts the eight bits of the EBCDIC character into the low order 8 bits (bits 24 – 31) of the destination register. The other bits are not changed.

There are many interesting uses
of this instruction. I elect to use this
to set the value in the register equal to the value of a digit. Thus if the character with EBCDIC
representation
X‘F7’
is in storage, I can set the value in the register to 7.
Placing the Numerical Value of a Digit in a Register
The first thing to do is get the EBCDIC code into the register. My solution uses the IC (Insert Character) instruction.
SR
R8,R8 CLEAR R8
IC R8,CARDIN+20(R3) GET THE DIGIT
In order to be sure that register R8 contains the EBCDIC code for the digit, I first clear the register to zero and then move the character. This step guarantees that bits 0 –23 of the register are 0 and that the value in the register, taken as a 32–bit fullword, is the EBCDIC code for the digit. I then subtract the value of the EBCDIC code for ‘0’ to get the value.
Another way to do this is load the register and use the logical instruction, with mnemonic N, to mask out all but the last hexadecimal digit. Here is the code.
IC
R8,CARDIN+20(R3) GET THE DIGIT
N
R8,=X‘F’
I now present my algorithm in fragments of code. We start with the beginning code. Each fragment will be listed along with its associated data declarations. This first code fragment just clears the result registers and checks to see if the input field, in the ten columns beginning at CARDIN+20, is all blanks.
If it is all blanks, the routine interprets the field as containing a 0 and returns.
NUMIN SR R7,R7 SET R7, THE RESULT, TO 0
SR
R6,R6 CLEAR HIGH-ORDER PRODUCT
MVI THESIGN,C‘P’ DEFAULT TO POSITIVE
CLC CARDIN+20(10),SPACE10 IS
THE INPUT ALL BLANKS
BE
DONE IF SO, JUST EXIT WITH
* THE VALUE SET TO 0.
* MORE CODE HERE
* 0123456789 BE SURE OF THE COUNT BELOW
SPACE10 DC CL‘ ’
JUST TEN SPACES
THESIGN DS CL1
The next part scans left to right looking for a non–blank character, which should be there. If none is found, it just quits. Admittedly, this should not happen, as we have tested and found at least one non–blank character in the input. This is defensive coding.
* NOW SCAN LEFT TO RIGHT TO FIND FIRST
NON-BLANK.
* USE BXLE WITH REGISTER PAIR (R4,R5).
*
SR
R3,R3 CLEAR
INDEX USED TO SCAN
* THE INPUT CHARACTER ARRAY
LA
R4,1 SET INCREMENT TO 1
LA R5,9 OFFSET
9 IS THE LAST DIGIT
SCAN1 CLI
CARDIN+20(R3),C‘ ’ DO WE HAVE A SPACE?
BNE NOTBLANK NO,
IT MAY BE A DIGIT
BXLE R3,R4,SCAN1 ITS BLANK.
LOOK AT NEXT
B
DONE ALL
BLANKS, WE ARE DONE
This next section of code checks the first non–blank character. If it is a minus sign, the sets a flag, which would be a Boolean in a high–level language. Here it is just the character “N”.
If the first non–blank character is a minus sign, then the next character is assumed to be the first digit. The index value is incremented by 1 to address the character after the “–”.
If the first non–blank character is not a minus sign, it is assumed to be a digit and processed as one. Note however that the processing loop explicitly makes two tests and processes the character only if it is not less than “0’ and not greater than “9”.
* AT THIS POINT, R3 IS THE INDEX OF THE
NON-BLANK
* CHARACTER. THE VALUES IN (R4,R5) ARE STILL VALID.
* IN PARTICULAR R4 STILL HAS VALUE 1.
*
NOTBLANK CLI CARDIN+20(R3),C‘-’ DO
WE HAVE A MINUS SIGN?
BNE ISDIG
MVI THESIGN,C‘N’ NOTE THE SIGN AS NEGATIVE
AR
R3,R4 ADD 1 TO VALUE IN R3.
CR
R3,R5 R3 HAS BEEN INCREMENTED
BH
DONE QUIT IF IT IS TOO BIG.
At this point, we know that CARDIN+20(R3)
references a non–blank character that
is in the range of card columns that might contain a digit. Here is the conversion loop. Note that the first four lines check to see
if the character is a digit by performing two tests equivalent to the compound
inequality ‘0’ £
Code £
‘9’. If the character is not a digit, it
is ignored and a branch to the end of the loop is taken.
ISDIG CLI CARDIN+20(R3),C‘0’ IS
IT A DIGIT
BL LOOP NO – CODE < ‘0’
CLI CARDIN+20(R3),C‘9’ AGAIN, IS IT A DIGIT?
BH LOOP NO – CODE > ‘9’
M R6,=F‘10’ MULTIPLY (R6,R7) BY 10
SR R8,R8 CLEAR R8
IC R8,CARDIN+20(R3) GET THE DIGIT
AR R7,R8 ADD TO THE PRODUCT
LOOP
BXLE R3,R4,ISDIG END OF THE
CLI THESIGN,C‘N’ WAS THE INPUT NEGATIVE
BNE DONE IT IS NOT NEGATIVE
LCR R7,R7 TAKE
2’S COMPLEMENT
DONE
* HERE R7 CONTAINS THE BINARY VALUE
Here is the complete code for NUMIN.
NUMIN SR
R7,R7 SET
R7, THE RESULT, TO 0
SR
R6,R6 CLEAR
HIGH-ORDER PRODUCT
MVI THESIGN,C‘P’ DEFAULT
TO POSITIVE
CLC CARDIN+20(10),SPACE10 IS THE INPUT ALL BLANKS
BE
DONE IF
SO, JUST EXIT WITH
* THE
VALUE SET TO 0.
*
* NOW SCAN LEFT TO RIGHT TO FIND FIRST
NON-BLANK.
* USE BXLE WITH REGISTER PAIR (R4,R5).
*
SR
R3,R3 CLEAR
INDEX USED TO SCAN
* THE INPUT CHARACTER ARRAY
LA
R4,1 SET INCREMENT TO 1
LA
R5,9 OFFSET 9 IS THE LAST DIGIT
SCAN1 CLI
CARDIN+20(R3),C‘ ’ DO WE
HAVE A SPACE?
BNE
NOTBLANK NO, IT MAY BE A DIGIT
BXLE R3,R4,SCAN1 ITS
BLANK. LOOK AT NEXT
B
DONE ALL
BLANKS, WE ARE DONE
*
* AT THIS POINT, R3 CONTAINS THE INDEX OF
THE NON-BLANK
* CHARACTER. THE VALUES IN (R4,R5) ARE STILL VALID.
* IN PARTICULAR R4 STILL HAS VALUE 1.
*
NOTBLANK CLI CARDIN+20(R3),C‘-’ DO WE HAVE A MINUS SIGN?
BNE
ISDIG
MVI
THESIGN,C‘N’ NOTE
THE SIGN AS NEGATIVE
AR
R3,R4 ADD
1 TO VALUE IN R3.
CR
R3,R5 R3
HAS BEEN INCREMENTED
BH
DONE QUIT
IF IT IS TOO BIG.
*
ISDIG CLI
CARDIN+20(R3),C‘0’ IS IT A DIGIT
BL
LOOP NO – CODE < ‘0’
CLI
CARDIN+20(R3),C‘9’ AGAIN, IS IT A DIGIT?
BH
LOOP NO – CODE > ‘9’
M
R6,=F‘10’ MULTIPLY (R6,R7) BY 10
SR
R8,R8 CLEAR R8
IC
R8,CARDIN+20(R3) GET THE DIGIT
AR
R7,R8 ADD TO THE PRODUCT
LOOP BXLE R3,R4,ISDIG END OF THE
CLI
THESIGN,C‘N’ WAS THE INPUT NEGATIVE
BNE
DONE IT IS NOT NEGATIVE
LCR
R7,R7 TAKE 2’S COMPLEMENT
*
DONE * HERE R7 CONTAINS THE BINARY VALUE
*
* 0123456789 BE SURE OF THE COUNT BELOW
SPACE10 DC CL‘ ’
JUST TEN SPACES
THESIGN DS CL1
Printing Packed Data
The standard solution to
convert binary integer data into printable form uses two
of the standard System/370 assembler language instructions.
CVD Converts the binary to packed decimal.
UNPK Converts the packed decimal to zoned decimal format.
The unpack command, UNPK, has an unfortunate side effect. Consider the decimal number 42, represented in binary in register R4.
CVD R4,PACKOUT produces the value in standard packed decimal format: 042C.
This should be unpacked to the EBCDIC F0 F4 F2
Unpack produces the zoned format F0 F4 C2.
This prints as “04B”, because 0xC2 is the EBCDIC code for the letter ‘B’.
Here is the code that works.
NUMOUT CVD R4,PACKOUT CONVERT THE NUMBER TO PACKED
UNPK THESUM,PACKOUT PRODUCE FORMATTED NUMBER
MVZ THESUM+7(1),=X’F0’ CHANGE THE ZONE FIELD AT
* ADDRESS THESUM+7
BR 8 RETURN ADDRESS IN REGISTER
8
PACKOUT DS PL8
HOLDS THE PACKED
OUTPUT
THESUM has eight characters stored as eight bytes. The addresses are:
|
SUM |
SUM +1 |
SUM +2 |
SUM +3 |
SUM +4 |
SUM +5 |
SUM +6 |
SUM +7 |
|
|
|
|
|
|
Hundreds |
Tens |
Units |
Again, the expression THESUM+7 is an address, not a value.
If THESUM holds C‘01234567’, then THESUM+7 holds C‘7’.
A Problem with the
Above Routine
Consider the decimal number –42, stored in a register in binary two’s–complement form.
CVD produces 042D
UNPK produces F0 F4 D2
The above MVZ will convert this to F0 F4 F2, a positive number. There are some easy fixes that are guaranteed to produce the correct representation for a negative number.
Most of the fixes using CVD and UNPK depend on placing the minus sign to the right of the digits. So that the negative integer –1234 would be printed as “1234–”.
My Version of NUMOUT (Number Out)
This routine avoids packed decimal numbers. We are given a binary number (negative or non–negative) in register R4.
1. Is the number negative?
If so, set the sign to ‘–’ and
take the absolute value.
Otherwise, leave the sign as
either ‘+’ or ‘ ’ (a blank).
We now have a non–negative number. Assume it is not zero.
2. Divide the number by 10, get a quotient and a
remainder.
The remainder will become the
character output.
3. The remainder is a positive number in the range
[0, 9].
Add =X‘F0’ to produce the
EBCDIC code.
4. Place this digit code in the proper output slot.
Is the quotient equal to 0? If so, quit.
If it is not zero, place the quotient in the dividend and return to 2.
Here is a paper example of the proper execution of the algorithm. Consider the positive integer 9413. Do repeated division by 10 and watch the remainders.
9413 divided by 10: Quotient = 941 Remainder = 3. Generate digit “3”.
941 divided by 10: Quotient = 94 Remainder = 1. Generate digit “1”.
94 divided by 10: Quotient = 9 Remainder = 4. Generate digit “4”.
9 divided by 10: Quotient = 0 Remainder = 9. Generate digit “9”.
Quotient is zero, so the process stops.
As they are generated, the digits are placed right to left, so that the result will print as the string “9413”. We now investigate the specifications for the code.
NUMOUT: Specifications
The code processes a 32–bit two’s–complement integer, stored as a fullword in register R5 and prints it out as a sequence of EBCDIC characters. The specification calls for printing out at most 10 digits, each as an EBCDIC character. The sign will be placed in the normal spot, just before the number. For no particular reason, positive numbers will be prefixed with a “+”. I just thought I would do something different.
This will use repeated division, using
the even–odd register pair (R4, R5), which contains a 64–bit dividend. As a part of our processing we shall insure
that the dividend is a 32–bit
positive number. In that case, the “high
order” 32 bits of the number are all 0.
For that reason, we initialize the “high
order” register, R4, to 0 and initialize the
“low order” register, R5, to the absolute value of the integer to be output.
The EBCDIC characters output will be
placed in a 12–byte area associated with
the label CHARSOUT,
at byte addresses CHARSOUT through CHARSOUT+11.
Review of the
Instructions: LCR and STC
Load Complement Register: LCR R1,R2
This loads register R1 with the negative (two’s–complement) of the value in register R2. This is also used in my routine NUMIN.
Store Character: STC R8,CHARSOUT(R3) PLACE THE DIGIT
This transfers the EBCDIC character, with code in the low order 8 bits of the source register, to the target address. None of the bits in the register are changed.
The idea behind NUMOUT is to compute the numerical value of a digit in a source register, convert it to an EBCDIC code, and move it to the print line. The first part checks the sign of the integer in register R4 and sets the sign character appropriately.
Note that the first thing to do is clear the output field to that expected for a zero result.
NUMOUT MVC
CHARSOUT,ZEROOUT DEFAULT TO 0
MVI THESIGN,C‘+’ DEFAULT TO A PLUS SIGN
C
R5,=F‘0’ COMPARE
R5 TO 0
BE
DONE VALUE
IS 0, NOTHING TO DO
BH
ISPOS VALUE
IS POSITIVE
MVI THESIGN,C‘-’ PLACE A MINUS SIGN
LCR R5,R5 2’S
COMPLEMENT R5 TO MAKE POS
ISPOS SR R4,R4 CLEAR
REGISTER 4
Here are some data declarations used with this part of the code.
*
123456789012
ZEROOUT DC C‘ 0’
11 SPACES AND A ZERO
CHARSOUT DS CL12 UP TO 11 DIGITS AND A SIGN
Division (Specifically
D – Divide Fullword)
This instruction divides a 64–bit
dividend, stored in an even–odd register pair,
by a fullword, and places the quotient and remainder back into the register
pair.
This will use the even–odd register pair
(R4, R5). The specifics of the
divide instruction are as follows.
|
|
R4 |
R5 |
|
Before division |
Dividend (high order 32 bits) |
Dividend (low order 32 bits) |
|
After division |
Remainder |
Quotient |
There are specific methods to handle dividends that might be negative.
As we are considering only positive dividends, we ignore these general methods.
Our Example of
Division
Start with a binary number in register R5.
We assume that register R4 has been
cleared to 0, as this example is limited to a 32–bit positive integer. This code will later be modified to process
the remainder, and store
the result as a printable EBCDIC character.
Here is the broad outline of the conversion loop, called DIVIDE because it achieves the result by repeated division by ten.
DIVIDE D R4,=F‘10’
DIVIDE (R4,R5) BY TEN
*
* THE REMAINDER, IN R4, MUST BE PROCESSED
AND STORED
*
SR R4,R4 CLEAR R4 FOR ANOTHER
C
R5,=F‘0’ CHECK THE QUOTIENT
BH DIVIDE CONTINUE IF QUOTIENT > 0
Placing the Digits
At this point, our register and storage usage is as follows:
1. Register R3 will be used as an index register.
2. Register pair (R4, R5) is being used for the division.
3. Register pair (R6, R7) is reserved for use by the BXH instruction.
CHARSOUT DS CL12
contains the twelve characters that
form the print representation
of
the integer. The number 12 is arbitrary;
it could be 10.
The strategy calls for first placing a digit in the units slot (overwriting the ‘0’) and then moving left to place other digits. To allow for a sign, no digit is to be placed in slot 0, at address CHARSOUT. The idea will be to place the character into a byte specified by CHARSOUT(R3).The register is initialized at 11 and decremented by 1 using the BXH instruction. What the code actually does is increment R3 by the negative value –1.

The Digit Placement Code
Here is a sketch of the digit placement code. It must be integrated into the larger DIVIDE loop in order to make sense. The register pair (R6, R7) is used for the BXH instruction.
R6 holds the increment value
R7 holds the limit value
L
R6,=F‘-1’ SET INCREMENT TO -1
SR
R7,R7 CLEAR R7.
LIMIT VALUE IS 0.
L
R3,=F‘11’ SET INDEX TO 11 FOR LAST DIGIT.
A
R4,=X‘F0’ ADD TO GET EBCDIC CODE
STC R4,CHARSOUT(R3) PLACE THE CHARACTER
BXH R3,R6,DIVIDE GO BACK TO TOP OF
MVC CHARSOUT(R3),THESIGN PLACE
THE SIGN
The Complete Divide
Loop
Here is the complete code for the divide loop. Note the branch out of the loop. The loop exits either when the quotient is 0 or when ten digits have been placed.
L
R6,=F‘-1’ SET INCREMENT TO -1
SR
R7,R7 CLEAR R7. LIMIT VALUE IS 0.
L
R3,=F‘11’ SET INDEX TO 11 FOR LAST
DIGIT
AT CHARSOUT+11.
*
DIVIDE D
R4,=F‘10’ DIVIDE (R4,R5) BY TEN AND
A
R4,=X‘F0’ ADD X ‘F0’, THE CODE FOR ‘0’
TO GET
EBCDIC CODE FOR DIGIT
STC R4,CHARSOUT(R3) PLACE THE CHARACTER
SR
R4,R4 CLEAR R4 FOR ANOTHER
C
R5,=F‘0’ CHECK THE QUOTIENT
BNH PUTSIGN EXIT LOOP IF QUOTIENT <= 0
BXH R3,R6,DIVIDE GO BACK TO TOP OF
*
PUTSIGN MVC CHARSOUT(R3),THESIGN PLACE
THE SIGN
Here is the complete code for NUMOUT.
*THE FIRST
PART SETS THE DEFAULTS AND PREPARES FOR A 0 OUTPUT
*
NUMOUT MVC CHARSOUT,ZEROOUT DEFAULT TO 0
MVI THESIGN,C‘+’ DEFAULT
TO A PLUS SIGN
C
R5,=F‘0’ COMPARE
R5 TO 0
BE
DONE VALUE
IS 0, NOTHING TO DO
BH
ISPOS VALUE
IS POSITIVE
MVI THESIGN,C‘-’ PLACE
A MINUS SIGN
LCR R5,R5 2’S
COMPLEMENT R5 TO MAKE POS
ISPOS SR
R4,R4 CLEAR
REGISTER 4
*
L
R6,=F‘-1’ SET INCREMENT TO -1
SR
R7,R7 CLEAR R7. LIMIT VALUE IS 0.
L
R3,=F‘11’ SET INDEX TO 11 FOR LAST
DIGIT AT
CHARSOUT+11.
*
DIVIDE D
R4,=F‘10’ DIVIDE (R4,R5) BY TEN AND
A
R4,=X‘F0’ ADD X ‘F0’, THE CODE FOR ‘0’
TO GET
EBCDIC CODE FOR DIGIT
STC R4,CHARSOUT(R3) PLACE THE CHARACTER
SR
R4,R4 CLEAR R4 FOR ANOTHER
C
R5,=F‘0’ CHECK THE QUOTIENT
BNH PUTSIGN EXIT LOOP IF QUOTIENT <= 0
BXH R3,R6,DIVIDE GO BACK TO TOP OF
*
PUTSIGN MVC CHARSOUT(R3),THESIGN PLACE THE SIGN IN THE SPOT
FOR
STANDARD ALGEBRA
*
* CODE HERE FOR RETURN FROM SUBROUTINE