Chapter 4 Appendix – CMOS Implementation of the Digital Gates

In this appendix to Chapter 3, we shall present the basics of the techniques used to fabricate the basic digital gates for implementation of Boolean functions. This material builds on the discussion “Review of Basic Electronics” found in Chapter 3, more particularly on the discussion of resistors in series.

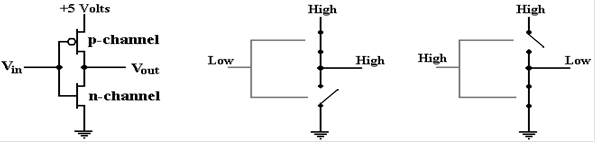
The term “CMOS” stands for “Complementary metal–oxide semiconductor”, referencing a technology in which MOS (metal–oxide semiconductor) transistors are used in complementary pairs as basic building blocks of a circuit. In a complementary transistor pair, one of the transistors is always “turned on”, while the other is “turned off”.

In any circuit, the output of a transistor depends on the input. In many common circuits, the transistor output is an amplification of the input; this is the common usage in radios and other audio devices. In the digital world, transistors are used as on–off switches. For a certain input, the transistor presents a very high resistance and can be considered as “turned off”. For other inputs, the transistor presents essentially no resistance and can be considered as “turned on”.

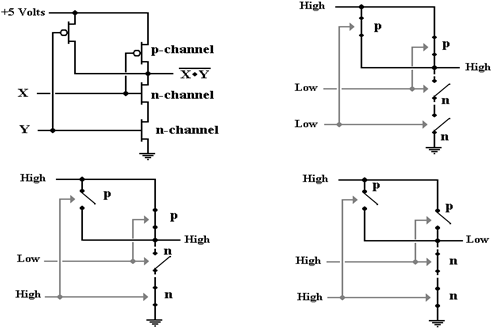
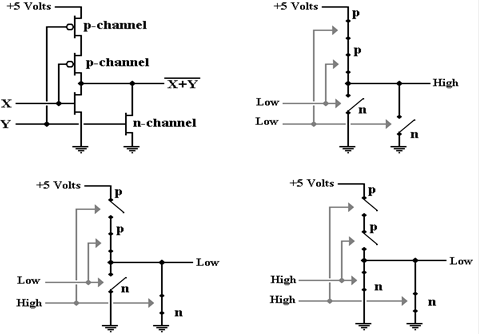
The basic CMOS transistor pair comprises a PMOS (Positive MOS) transistor connected to a NMOS (Negative MOS) transistor. The inputs to the two transistors are tied together. An input that turns one of the pair on will turn the other of the pair off.

In order to examine this effect more closely, we first return to the basic series resistor circuit in Chapter 3. Here we consider a voltage source, with voltage designated by “E” driving a two resistor circuit, and ask about the value of E₂, the voltage at point 2.

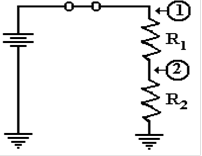In general, E₂ = (E·R₂) / (R₁ + R₂), the value being somewhere between the full voltage and ground voltage, defined to be zero.

If R₁ = 0 and R₂ ≠ 0, then E₂ = E, the full voltage.

If R₁ ≠ 0 and R₂ = 0, then E₂ = 0.

If R₁ = 0 and R₂ = 0, then there is a short circuit, and the battery burns up. This is not a desirable condition.

The basic idea behind these circuits can be seen in the following circuit, which is an adaptation of the one just above.

When the top switch is closed (R₁ = 0) and the bottom switch is open (R₂ ≠ 0), the voltage E₂ is the full voltage. When the top is open and the bottom closed, E₂ = 0.

We now examine a CMOS implementation of the NOT gate. This has one pair of complementary transistors, the PMOS (labeled “p–channel”) and the NMOS
(labeled “n–channel”). Note the behavior of the pair of transistors as the input voltage V_in is changed between +5 volts (high) and 0 volts (low).

When V_in is low (0 volts, or logic 0), the output V_out is high (+5 volts, or logic 1).

When V_in is high (+5 volts, or logic 1), the output V_out is low (0 volts, or logic 0).

Viewed as a logic signal, the output is the complement of the input. This is a NOT gate.

In order to fabricate the AND and OR gates, we must first do NAND and NOR. We then
use the fact that AND = NOT (NAND) and OR = NOT (NOR). Here is the NAND gate.

Note that the output is low (logic 0) only when both of the inputs are high. If one or more of the inputs is low (logic 0), then one or more of the NMOS transistors (labeled “n–channel”) will be non–conductive, acting as an open switch, and the output is high (logic 1).

Here is the CMOS implementation of the NOR gate.

Note that the output is high (logic 1) only when both of the inputs are low (logic 0).
If either input is high (logic 1), then the output is low (logic 0). This is a NOR gate.

Here are the CMOS implementations of the AND (as NOT(NAND)), and OR
(as NOT(NOR)) gates.