Chapter 4 – Boolean Algebra and Some Combinational Circuits

Chapter Overview

This chapter discusses combinational circuits that are basic to the functioning of a digital
computer. With one exception, these circuits either directly implement the basic Boolean
functions or are built from basic gates that directly implement these functions. For that
reason, we review the fundamentals of Boolean algebra.

Chapter Assumptions

The intended audience for this chapter (and the rest of the course) will have a basic
understanding of Boolean algebra and some understanding of electrical circuitry. The
student should have sufficient familiarity with each of these subjects to allow him or her
to follow their use in the lecture material.

One of the prerequisites for this course is CPSC 2105 – Introduction to Computer
Organization. Topics covered in that course include the basic Boolean functions; their
representation in standard forms, including POS (Product of Sums) and SOP (Sum of
Products); and the basic postulates and theorems underlying the algebra. Due to the
centrality of Boolean algebra to the combinational circuits used in computer design, this
subject will be reviewed in this chapter.

Another topic that forms a prerequisite for this course is a rudimentary familiarity with
electrical circuits and their components. This course will focus on the use of TTL
(Transistor–Transistor Logic) components as basic units of a computer. While it is sufficient
for this course for the student to remember “TTL” as the name of a technology used to
implement digital components, it would be preferable if the student were comfortable with
the idea of “transistor” and what it does.

Another assumption for this chapter is that the student has an intuitive feeling for the ideas of
voltage and current in an electrical circuit. An understanding of Ohm’s law (V = I·R) would
be helpful here, but is not required. More advanced topics, such as Kickoff’s laws will not
even be mentioned in this discussion, although they are very useful in circuit design. It is
sufficient for the student to be able to grasp statements such as the remark that in active-high
TTL components, logic 1 is represented by +5 volts and logic 0 by 0 volts.

Boolean Algebra

We begin this course in computer architecture with a review of topics from the prerequisite
course. It is assumed that the student is familiar with the basics of Boolean algebra and
two’s complement arithmetic, but it never hurts to review.

Boolean algebra is the algebra of variables that can assume two values: True and False.
Conventionally we associate these as follows: True = 1 and False = 0. This association will
become important when we consider the use of Boolean components to synthesize arithmetic
circuits, such as a binary adder.

Formally, Boolean algebra is defined over a set of elements {0, 1}, two binary operators

{AND, OR}, and a single unary operator NOT. These operators are conventionally
represented as follows: · for AND

+ for OR

’ for NOT, thus X’ is Not(X).

The Boolean operators are completely defined by Truth Tables.

AND 0·0 = 0 OR 0+0 = 0 NOT 0’ = 1
0·1 = 0 0+1 = 1 1’ = 0
1·0 = 0 1+0 = 1
1·1 = 1 1+1 = 1

Note that the use of “+” for the OR operation is restricted to those cases in which addition
is not being discussed. When addition is also important, we use different symbols for the
binary Boolean operators, the most common being Ù for AND, and Ú for OR.

There is another notation for the complement (NOT) function that is preferable. If X is a
Boolean variable, then is its complement, so that = 1 and = 0. The only reason that
this author uses X’ to denote is that the former notation is easier to create in MS-Word.

There is another very handy function, called the XOR (Exclusive OR) function. Although it
is not basic to Boolean algebra, it comes in quite handy in circuit design. The symbol for the
Exclusive OR function is Å. Here is its complete definition using a truth table.

0 Å 0 = 0 0 Å 1 = 1
1 Å 0 = 1 1 Å 1 = 0

Truth Tables

A truth table for a function of N Boolean variables depends on the fact that there are only 2^N
different combinations of the values of these N Boolean variables. For small values of N,
this allows one to list every possible value of the function.

Consider a Boolean function of two Boolean variables X and Y. The only possibilities for
the values of the variables are:

X = 0 and Y = 0

X = 0 and Y = 1

X = 1 and Y = 0

X = 1 and Y = 1

Similarly, there are eight possible combinations of the three variables X, Y, and Z, beginning
with X = 0, Y = 0, Z = 0 and going through X = 1, Y = 1, Z = 1. Here they are.
X = 0, Y = 0, Z = 0 X = 0, Y = 0, Z = 1 X = 0, Y = 1, Z = 0 X = 0, Y = 1, Z = 1
X = 1, Y = 0, Z = 0 X = 1, Y = 0, Z = 1 X = 1, Y = 1, Z = 0 X = 1, Y = 1, Z = 1

As we shall see, we prefer truth tables for functions of not too many variables.

X	Y	F(X, Y)
0	0	1
0	1	0
1	0	0
1	1	1

The figure at left is a truth table for a two-variable function. Note that
we have four rows in the truth table, corresponding to the four possible
combinations of values for X and Y. Note also the standard order in
which the values are written: 00, 01, 10, and 11. Other orders can be
used when needed (it is done below), but one must list all combinations.

X	Y	Z	F1	F2
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

For another example of truth tables, we consider the figure above, which shows two Boolean
functions of three Boolean variables. Truth tables can be used to define more than one
function at a time, although they become hard to read if either the number of variables
or the number of functions is too large. Here we use the standard shorthand of F1 for
F1(X, Y, Z) and F2 for F2(X, Y, Z). Also note the standard ordering of the
rows, beginning with 0 0 0 and ending with 1 1 1. This causes less confusion than
other ordering schemes, which may be used when there is a good reason for them.

As an example of a truth table in which non-standard ordering might be useful, consider the
following table for two variables. As expected, it has four rows.

X	Y	X · Y	X + Y
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	1

A truth table in this non-standard ordering would be used to
prove the standard Boolean axioms:
X · 0 = 0 for all X X + 0 = X for all X

X · 1 = X for all X X + 1 = 1 for all X

In future lectures we shall use truth tables to specify functions without needing to consider
their algebraic representations. Because 2^N is such a fast growing function, we give truth
tables for functions of 2, 3, and 4 variables only, with 4, 8, and 16 rows, respectively. Truth
tables for 4 variables, having 16 rows, are almost too big. For five or more variables, truth
tables become unusable, having 32 or more rows.

Labeling Rows in Truth Tables

We now discuss a notation that is commonly used to identify rows in truth tables. The exact
identity of the rows is given by the values for each of the variables, but we find it convenient
to label the rows with the integer equivalent of the binary values. We noted above that for N
variables, the truth table has 2^N rows. These are conventionally numbered from 0 through
2^N – 1 inclusive to give us a handy way to reference the rows. Thus a two variable truth table
would have four rows numbered 0, 1, 2, and 3. Here is a truth-table with labeled rows.

Row	A	B	G(A, B)
0	0	0	0
1	0	1	1
2	1	0	1
3	1	1	0

We can see that G(A, B) = A Å B, but

0 = 0·2 + 0·1 this value has nothing to do with the

1 = 0·2 + 1·1 row numberings, which are just the

2 = 1·2 + 0·1 decimal equivalents of the values in

3 = 1·2 + 1·1 the A & B columns as binary.

A three variable truth table would have eight rows, numbered 0, 1, 2, 3, 4, 5, 6, and 7.
Here is a three variable truth table for a function F(X, Y, Z) with the rows numbered.

Row Number	X	Y	Z	F(X, Y, Z)
0	0	0	0	1
1	0	0	1	1
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

Note that the row numbers correspond to the
decimal value of the three bit binary, thus

0 = 0·4 + 0·2 + 0·1

1 = 0·4 + 0·2 + 1·1

2 = 0·4 + 1·2 + 0·1

3 = 0·4 + 1·2 + 1·1

4 = 1·4 + 0·2 + 0·1

5 = 1·4 + 0·2 + 1·1

6 = 1·4 + 1·2 + 0·1

7 = 1·4 + 1·2 + 1·1

Truth tables are purely Boolean tables in which decimal numbers, such as the row numbers
above do not really play a part. However, we find that the ability to label a row with a
decimal number to be very convenient and so we use this. The row numberings can be quite
important for the standard algebraic forms used in representing Boolean functions.

Question: Where to Put the Ones and Zeroes

Every truth table corresponds to a Boolean expression. For some truth tables, we begin with
a Boolean expression and evaluate that expression in order to find where to place the 0’s and
1’s. For other tables, we just place a bunch of 0’s and 1’s and then ask what Boolean
expression we have created. The truth table just above was devised by selecting an
interesting pattern of 0’s and 1’s. The author of these notes had no particular pattern in
mind when creating it. Other truth tables are more deliberately generated.

Let’s consider the construction of a truth table for the Boolean expression.

F(X, Y, Z) =

Let’s evaluate this function for all eight possible values of X, Y, Z.
X = 0 Y = 0 Z = 0 F(X, Y, Z) = 0·0 + 0·0 + 0·1·0 = 0 + 0 + 0 = 0
X = 0 Y = 0 Z = 1 F(X, Y, Z) = 0·0 + 0·1 + 0·1·1 = 0 + 0 + 0 = 0
X = 0 Y = 1 Z = 0 F(X, Y, Z) = 0·1 + 1·0 + 0·0·0 = 0 + 0 + 0 = 0
X = 0 Y = 1 Z = 1 F(X, Y, Z) = 0·1 + 1·1 + 0·0·1 = 0 + 1 + 0 = 1
X = 1 Y = 0 Z = 0 F(X, Y, Z) = 1·0 + 0·0 + 1·1·0 = 0 + 0 + 0 = 0
X = 1 Y = 0 Z = 1 F(X, Y, Z) = 1·0 + 0·1 + 1·1·1 = 0 + 0 + 1 = 1
X = 1 Y = 1 Z = 0 F(X, Y, Z) = 1·1 + 1·0 + 1·0·0 = 1 + 0 + 0 = 1
X = 1 Y = 1 Z = 1 F(X, Y, Z) = 1·1 + 1·1 + 1·0·1 = 1 + 1 + 0 = 1

From the above, we create the truth table for the function. Here it is.

X	Y	Z	F(X, Y, Z)
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

A bit later we shall study how to derive Boolean expressions from a truth table. Truth tables
used as examples for this part of the course do not appear to be associated with a specific
Boolean function. Often the truth tables are associated with well-known functions, but the
point is to derive that function starting only with 0’s and 1’s.

Consider the truth table given below, with no explanation of the method used to generate the
values of F1 and F2 for each row.

Row	X	Y	Z	F1	F2
0	0	0	0	0	0
1	0	0	1	1	0
2	0	1	0	1	0
3	0	1	1	0	1
4	1	0	0	1	0
5	1	0	1	0	1
6	1	1	0	0	1
7	1	1	1	1	1

Figure: Our Sample Functions F1 and F2

Students occasionally ask how the author knew where to place the 0’s and 1’s in the above
table. There are two answers to this, both equally valid. We reiterate the statement that a
Boolean function is completely specified by its truth table. Thus, one can just make an
arbitrary list of 2^N 0’s and 1’s and then decide what function of N Boolean variables has
been represented. In that view, the function F2 is that function specified by the sequence
(0, 0, 0, 1, 0, 1, 1, 1) and nothing more. We can use methods described below to assign it a
functional representation. Note that F2 is 1 if and only if two of X, Y, and Z are 1. Given
this, we can give a functional description of the function as F2 = X·Y + X·Z + Y·Z.

As the student might suspect, neither the pattern of 0’s and 1’s for F1 nor that for F2 were
arbitrarily selected. The real answer is that the instructor derived the truth table from a set of
known Boolean expressions, one for F1 and one for F2. The student is invited to compute
the value of F2 = X·Y + X·Z + Y·Z for all possible values of X, Y, and Z; this will verify
the numbers as shown in the truth table.

We have noted that a truth table of two variables has four rows (numbered 0, 1, 2, and 3)
and that a truth table of three variables has eight rows (numbered 0 through 7). We now
prove that a truth table of N variables has 2^N rows, numbered 0 through 2^N – 1. Here is an
inductive proof, beginning with the case of one variable.

1. Base case: a function of one variable X requires 2 rows,
one row for X = 0 and one row for X = 1.

2. If a function of N Boolean variables X₁, X₂, …., X_N requires 2^N rows, then
the function of (N + 1) variables X₁, X₂, …., X_N, X_N+1 would require

2^N rows for X₁, X₂, …., X_N when X_N+1 = 0

2^N rows for X₁, X₂, …., X_N when X_N+1 = 1

3. 2^N +2^N = 2^N+1, so the function of (N + 1) variables required 2^N+1 rows.

While we are at it, we show that the number of Boolean functions of N Boolean variables is
2^R where R = 2^N, thus the number is . The argument is quite simple. We have shown
that the number of rows in a truth table is given by R = 2^N. The value in the first row could
be a 0 or 1; thus two choices. Each of the R = 2^N rows could have two choices, thus the total
number of functions is 2^R where R = 2^N.

For N = 1, R = 2, and 2² = 4. A truth table for the function F(X) would have two rows, one
for X = 0 and one for X = 1. There are four functions of a single Boolean variable.
F₁(X) = 0, F₂(X) = 1, F₃(X) = X, and F₄(X) = .

It might be interesting to give a table of the number of rows in a truth table and number of
possible Boolean functions for N variables. The number of rows grows quickly, but the
number of functions grows at an astonishing rate.

N	R = 2^N	2^R
1	2	4
2	4	16
3	8	256
4	16	65 536
5	32	4 294 967 296
6	64	2^64 » 1.845·10^19

Note on computation: log 2 = 0.30103, so 2⁶⁴ = (10^0.30103)⁶⁴ = 10^19.266 .
log 1.845 = 0.266, so 10^0.266 » 1.845 and 10^19.266 » 1.845·10¹⁹

The number of Boolean functions of N Boolean variables is somewhat of interest. More to
interest in this course is the number of rows in any possible truth-table representation of a
function of N Boolean variables. For N = 2, 3, and 4, we have 2^N = 4, 8, and 16 respectively,
so that truth tables for 2, 3, and 4 variables are manageable. Truth tables for five variables
are a bit unwieldy and truth tables for more than five variables are almost useless.

Truth Tables and Associated Tables with Don’t Care Conditions

At this point, we mention a convention normally used for writing large truth tables and
associated tables in which there is significant structure. This is called the “don’t care”
condition, denoted by a “d” in the table. When that notation appears, it indicates that the
value of the Boolean variable for that slot can be either 0 or 1, but give the same effect.

Let’s look at two tables, each of which to be seen and discussed later in this textbook. We
begin with a table that is used to describe control of memory; it has descriptive text.

Select		Action
0	0	Memory not active
0	1	Memory not active
1	0	CPU writes to memory
1	1	CPU reads from memory

The two control variables are Select and . But note that when Select = 0, the action of
the memory is totally independent of the value of . For this reason, we may write:

Select		Action
0	d	Memory not active
1	0	CPU writes to memory
1	1	CPU reads from memory

Consider the truth table for a 2–to–4 active–high decoder that is enabled high. The
complete version is shown first; it has 8 rows and describes 4 outputs:Y₀, Y₁, Y₂, and Y₃.

Enable	X1	X0	Y0	Y1	Y2	Y3
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	0	0	0
0	1	1	0	0	0	0
1	0	0	1	0	0	0
1	0	1	0	1	0	0
1	1	0	0	0	1	0
1	1	1	0	0	0	1

The more common description uses the “don’t care” notation.

Enable	X1	X0	Y0	Y1	Y2	Y3
0	d	d	0	0	0	0
1	0	0	1	0	0	0
1	0	1	0	1	0	0
1	1	0	0	0	1	0
1	1	1	0	0	0	1

This latter form is simpler to read. The student should not make the mistake of considering
the “d” as an algebraic value. What the first row says is that if Enable = 0, then I don’t care
what X₁ and X₀ are; even if they have different values, all outputs are 0.

The next section will discuss conversion of a truth table into a Boolean expression. The
safest way to do this is to convert a table with “don’t cares” back to the full representation.

Evaluation of Boolean Expressions

Here is another topic that this instructor normally forgets to mention, as it is so natural to
one who has been in the “business” for many years. The question to be addressed now is:
“What are the rules for evaluating Boolean expressions?”

Operator Precedence

The main question to be addressed is the relative precedence of the basic Boolean operators:
AND, OR, and NOT. These rules are based on the algebraic model, which does not use the
XOR function; its precedence is not defined. The relative precedence in any programming
language is specified by that language.

The relative precedence of the operators is:
1) NOT do this first
2) AND
3) OR do this last

Consider the Boolean expression A·B + C·D, often written as AB + CD. Without the
precedence rules, there are two valid interpretations: either (A·B) + (C·D) or A·(B + C)·D.
The precedence rules for the operators indicate that the first is the correct interpretation; in
this Boolean algebra follows standard algebra as taught in high-school. Consider now the
expression ; according to our rules, this is read as .

Note that parentheses and explicit extension of the NOT overbar can override the precedence
rules, so that A·(B + C)·D is read as the logical AND of three terms: A, (B + C), and D.
Note also that the two expressions and are different. The first expression, better
written as , refers to the logical NOT of the logical AND of A and B; in a language
such as LISP it would be written as NOT (AND A B). The second expression, due to the
precedence rules, refers to the logical AND of the logical NOT of A and the logical NOT
of B; in LISP this might be written as AND( (NOT A) (NOT B) ).

Evaluation of Boolean expressions implies giving values to the variables and following the
precedence rules in applying the logical operators. Let A = 1, B = 0, C = 1, and D = 1.

A·B + C·D = 1·0 + 1·1 = 0 + 1 = 1
A·(B + C)·D = 1·(0 + 1)·1 = 1 · 1 · 1 = 1
= = 0 · 0 + 1 · 0 = 0 + 0 = 0
= = = 1
= = 0 · 1 = 0

Also

A·(B + C·D) = 1·(0 + 1·1) = 1 · (0 + 1) = 1 · 1 = 1
(A·B + C)·D = (1·0 + 1)·1 = (0 + 1) · 1 = 1

The Basic Axioms and Postulates of Boolean Algebra

We close our discussion of Boolean algebra by giving a formal definition of the algebra
along with a listing of its basic axioms and postulates.

Definition: A Boolean algebra is a closed algebraic system containing a set K of two or more
elements and three operators, two binary and one unary. The binary operators are denoted
“+” for OR and “·” for AND. The unary operator is NOT, denoted by a overbar placed over
the variable. The system is closed, so that for all X and Y in K, we have X + Y in K, X · Y
in K and NOT(X) in K. The set K must contain two constants 0 and 1 (FALSE and TRUE),
which obey the postulates below. In normal use, we say K = {0, 1} – set notation.

The postulates of Boolean algebra are:
P1 Existence of 0 and 1 a) X + 0 = X for all X
b) X · 1 = X for all X

P2 Commutativity a) X + Y = Y + X for all X and Y
b) X · Y = Y · X for all X and Y

P3 Associativity a) X + (Y + Z) = (X + Y) + Z, for all X, Y, and Z
b) X · (Y · Z) = (X · Y) · Z, for all X, Y, and Z

P4 Distributivity a) X · (Y + Z) = (X · Y) + (X · Z), for all X, Y, Z
b) X + (Y · Z) = (X + Y) · (X + Z), for all X, Y, Z

P5 Complement a) X + = 1, for all X
b) X · = 0, for all X

The theorems of Boolean algebra are:
T1 Idempotency a) X + X = X, for all X
b) X · X = X, for all X

T2 1 and 0 Properties a) X + 1 = 1, for all X
b) X · 0 = 0, for all X

T3 Absorption a) X + (X · Y) = X, for all X and Y

b) X · (X + Y) = X, for all X and Y

T4 Absorption a) X + ·Y = X + Y, for all X and Y
b) X · ( + Y) = X · Y, for all X and Y

T5 DeMorgan’s Laws a) = ·
b) = +

T6 Consensus a)

b)

The observant student will note that most of the postulates, excepting only P4b, seem to be
quite reasonable and based on experience in high-school algebra. Some of the theorems
seem reasonable or at least not sufficiently different from high school algebra to cause
concern, but others such as T1 and T2 are decidedly different. Most of the unsettling
differences have to do with the properties of the Boolean OR function, which is quite
different from standard addition, although commonly denoted with the same symbol.

The principle of duality is another property that is unique to Boolean algebra – there is
nothing like it in standard algebra. This principle says that if a statement is true in Boolean
algebra, so is its dual. The dual of a statement is obtained by changing ANDs to ORs, ORs
to ANDs, 0s to 1s, and 1s to 0s. In the above, we can arrange the postulates as duals.

Postulate Dual
0·X = 0 1 + X = 1
1·X = X 0 + X = X
0 + X = X 1·X = X These last two statements just repeat
1 + X = 1 0·X = 0 the first two if one reads correctly.

Both standard algebra and Boolean algebra have distributive postulates. Standard algebra
has one distributive postulate; Boolean algebra must have two distributive postulates as a
result of the principle of duality.

In standard algebra, we have the equality A·(B + C) = A·B + A·C for all values of A, B, and
C. This is the distributive postulate as seen in high school; we know it and expect it.

In Boolean algebra we have the distributive postulate A·(B + C) = A·B + A·C, which looks
familiar. The principle of duality states that if A·(B + C) = A·B + A·C is true then the dual
statement A + B·C = (A + B)·(A + C) must also be true. We prove the second statement
using a method unique to Boolean algebra. This method depends on the fact that there are
only two possible values for A: A = 0 and A = 1. We consider both cases using a proof
technique much favored by this instructor: consider both possibilities for one variable.

If A = 1, the statement becomes 1 + B·C = (1 + B)·(1 + C), or 1 = 1·1, obviously true.

If A = 0, the statement becomes 0 + B·C = (0 + B)·(0 + C), or B·C = B·C.

Just for fun, we offer a truth-table proof of the second distributive postulate.

A	B	C	B·C	A + B·C	(A + B)	(A + C)	(A + B)·(A + C)
0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0
0	1	0	0	0	1	0	0
0	1	1	1	1	1	1	1
1	0	0	0	1	1	1	1
1	0	1	0	1	1	1	1
1	1	0	0	1	1	1	1
1	1	1	1	1	1	1	1

Figure: A + B·C = (A + B)·(A + C)

Note that to complete the proof, one must construct the truth table, showing columns for
each of the two functions A + B·C and (A + B)·(A + C), then note that the contents of the
two columns are identical for each row.

A Few More Proofs

At this point in the course, we note two facts:
1) That some of the theorems above look a bit strange.
2) That we need more work on proof of Boolean theorems.

Towards that end, let’s look at a few variants of the Absorption Theorem. We prove that

X + (X · Y) = X, for all X and Y

The first proof will use a truth table. Remember that the truth table will have four rows,
corresponding to the four possible combinations of values for X and Y:

X = 0 and Y = 0, X = 0 and Y = 1, X = 1 and Y = 0, X = 1 and Y = 1.

X	Y	X · Y	X + (X · Y)
0	0	0	0
0	1	0	0
1	0	0	1
1	1	1	1

Having computed the value of X + (X · Y) for all
possible combinations of X and Y, we note that in each
case we have X + (X · Y) = X. Thus, we conclude that
the theorem is true.

Here is another proof method much favored by this author. It depends on the fact that there
are only two possible values of X: X = 0 and X = 1. A theorem involving the variable X is
true if and only if it is true for both X = 0 and X = 1. Consider the above theorem, with the
claim that X + (X · Y) = X. We look at the cases X = 0 and X = 1, computing both the LHS
(Left Hand Side of the Equality) and RHS (Right Hand Side of the Equality).

If X = 0, then X + (X · Y) = 0 + (0 · Y) = 0 + 0 = 0, and LHS = RHS.
If X = 1, then X + (X · Y) = 1 + (1 · Y) = 1 + Y = 1, and LHS = RHS.

Consider now a trivial variant of the absorption theorem.

+ ( · Y) = , for all X and Y

There are two ways to prove this variant of the theorem., given that the above standard
statement of the absorption theorem is true. An experienced mathematician would claim
that the proof is obvious. We shall make it obvious.

The absorption theorem, as proved, is X + (X · Y) = X, for all X and Y. We restate the
theorem, substituting the variable W for X, getting W + (W · Y) = W, for all X and Y.
Now, we let W = , and the result is indeed obvious.

X	Y	· Y	X + ( · Y)	X + Y
0	0	0	0	0
0	1	1	1	1
1	0	0	1	1
1	1	0	1	1

We close this section with a proof of the other
standard variant of the absorption theorem,
that X + ( · Y) = X + Y for all X and Y.
The theorem can also be proved using the
two case method.

Yet Another Sample Proof

While this instructor seems to prefer the obscure “two-case” method of proof, most
students prefer the truth table approach. We shall use the truth table approach to
prove one of the variants of DeMorgan’s laws: = + .

X	Y	X · Y				+	Comment
0	0	0	1	1	1	1	Same
0	1	0	1	1	0	1	Same
1	0	0	1	0	1	1	Same
1	1	1	0	0	0	0	Same

In using a truth table to show that two expressions are equal, one generates a column for each
of the functions and shows that the values of the two functions are the same for every
possible combination of the input variables. Here, we have computed the values of both
and ( + ) for all possible combinations of the values of X and Y and shown that
for every possible combination the two functions have the same value. Thus they are equal.

Some Basic Forms: Product of Sums and Sum of Products

We conclude our discussion of Boolean algebra by giving a formal definition to two
notations commonly used to represent Boolean functions:

SOP Sum of Products
POS Product of Sums

We begin by assuming the definition of a variable. A literal is either a variable in its true
form or its complemented form, examples are A, C’, and D. A product term is the logical
AND of one or more literals; a sum term is the logical OR of one or more literals.
According to the strict definition the single literal B’ is both a product term and sum term.

A sum of products (SOP) is the logical OR of one or more product terms.

A product of sums (POS) is the logical AND of one or more sum terms.

Sample SOP: A + B·C A·B + A·C + B·C A·B + A·C + A·B·C

Sample POS: A·(B + C) (A + B)·(A + C)·(B + C) (A + B)·(A + C)·(A + B + C)

The student will note a few oddities in the above definition. These are present in order to
avoid special cases in some of the more general theorems. The first oddity is the mention of
the logical AND of one term and the logical OR of one term; each of these operators is a
binary operator and requires two input variables. What we are saying here is that if we take a
single literal as either a sum term or a product term, our notation is facilitated. Consider the
expression (A + B + C), which is either a POS or SOP expression depending on its use. As a
POS expression, it is a single sum term comprising three literals. As an SOP expression, it is
the logical OR of three product terms, each of which comprising a single literal. For cases
such as these the only rule is to have a consistent interpretation.

We now consider the concept of normal and canonical forms. These forms apply to both
Sum of Products and Produce of Sums expressions, so we may have quite a variety of
expression types including the following.

1. Not in any form at all.
2. Sum of Products, but not normal.
3. Product of Sums, but not normal.
4. Normal Sum of Products.
5. Normal Product of Sums.
6. Canonical Sum of Products.
7. Canonical Product of Sums.

In order to define the concept of a normal form, we must consider the idea of inclusion.

A product term X is included in another product term Y if every literal that is in X is also in
Y. A sum term X is included in another sum term Y if every literal that is in X is also in Y.
For inclusion, both terms must be product terms or both must be sum terms. Consider the
SOP formula A·B + A·C + A·B·C. Note that the first term is included in the third term as
is the second term. The third term A·B·C contains the first term A·B, etc.

Consider the POS formula (A + B)·(A + C)·(A + B + C). Again, the first term (A + B) is
included in the third term (A + B + C), as is the second term.

An extreme form of inclusion is observed when the expression has identical terms.
Examples of this would be the SOP expression A·B + A·C + A·B and the POS expression
(A + B)·(A + C)·(A + C). Each of these has duplicate terms, so that the inclusion is 2-way.
The basic idea is that an expression with included (or duplicate) terms is not written in the
simplest possible form. The idea of simplifying such expressions arises from the theorems
of Boolean algebra, specifically the following two.

T1 Idempotency a) X + X = X, for all X
b) X · X = X, for all X

T3 Absorption a) X + (X · Y) = X, for all X and Y

b) X · (X + Y) = X, for all X and Y

As a direct consequence of these theorems, we can perform the following simplifications.

A·B + A·C + A·B = A·B + A·C
(A + B)·(A + C)·(A + C) = (A + B)·(A + C)
A·B + A·C + A·B·C = A·B + A·C
(A + B)·(A + C)·(A + B + C) = (A + B)·(A + C)

We now consider these two formulae with slight alterations: A·B + A·C + A’·B·C and
(A + B)·(A + C)·(A’ + B + C). Since the literal must be included exactly, neither of
formulae in this second set contains included terms.

We now can produce the definitions of normal forms. A formula is in a normal form only
if it contains no included terms; thus, a normal SOP form is a SOP form with no included
terms and a normal POS form is a POS form with no included terms.

Sample Normal SOP: A + B·C A·B + A·C + B·C A’·B + A·C + B·C’

Sample Normal POS: A·(B + C) (A + B)·(A + C)·(B + C) (A’ + B)·(A + C’)

We now can define the canonical forms. A normal form over a number of variables is in
canonical form if every term contains each variable in either the true or complemented form.
A canonical SOP form is a normal SOP form in which every product term contains a literal
for every variable. A canonical POS form is a normal POS form in which every sum term
in which every sum term contains a literal for every variable.

Note that all canonical forms are also normal forms. Canonical forms correspond directly to
truth tables and can be considered as one-to-one translations of truth tables. Here are the
rules for converting truth tables to canonical forms.

To produce the Sum of Products representation from a truth table, follow this rule.

a) Generate a product term for each row where the value of the function is 1.
b) The variable is complemented if its value in the row is 0, otherwise it is not.

To produce the Product of Sums representation from a truth table, follow this rule.
a) Generate a sum term for each row where the value of the function is 0.
b) The variable is complemented if its value in the row is 1, otherwise it is not.

As an example of conversion from a truth table to the normal forms, consider the two
Boolean functions F1 and F2, each of three Boolean variables, denoted A, B, and C.
Note that a truth table for a three-variable function requires 2³ = 8 rows.

Row	A	B	C	F1	F2
0	0	0	0	0	0
1	0	0	1	1	0
2	0	1	0	1	0
3	0	1	1	0	1
4	1	0	0	1	0
5	1	0	1	0	1
6	1	1	0	0	1
7	1	1	1	1	1

Recall that the truth table forms a complete specification of both F1 and F2. We may elect
to represent each of F1 and F2 in either normal or canonical form, but that is not required.

There are two ways to represent the canonical forms. We first present a pair of forms that
this author calls the S–list and P–list. The S–list is used to represent canonical SOP and the
P–list is used to represent canonical POS forms.

To generate the S–list, we just list the rows of the truth table for which the function has a
value of 1. In the truth table, we have the following.
F1 has value 1 for rows 1, 2, 4, and 7; so F1 = S(1, 2, 4, 7).
F2 has value 1 for rows 3, 5, 6, and 7; so F2 = S(3, 5, 6, 7).

To generate the P–list, we just list the rows of the truth table for which the function has a
value of 0. In the truth table, we have the following.
F1 has value 1 for rows 0, 3, 5, and 6; so F1 = P(0, 3, 5, 6).
F2 has value 1 for rows 0, 1, 2, and 4; so F2 = P(0, 1, 2, 4).

Note that conversion directly between the S–list and P–list forms is easy if one knows how
many variables are involved. Here we have 3 variables, with 8 rows numbered 0 through 7.
Thus, if F1 = S(1, 2, 4, 7), then F1 = P(0, 3, 5, 6) because the numbers 0, 3, 5, and 6 are the
only numbers in the range from 0 to 7 inclusive that are not in the S–list. The conversion
rule works both ways. If F2 = P(0, 1, 2, 4), then F2 = S(3, 5, 6, 7) because the numbers
3, 5, 6, and 7 are the only numbers in the range from 0 to 7 inclusive not in the P–list.

We now address the generation of the canonical SOP form of F1 from the truth table. The
rule is to generate a product term for each row for which the function value is 1. Reading
from the top of the truth table, the first row of interest is row 1.

A	B	C	F1
0	0	1	1

We have A = 0 for this row, so the corresponding literal in the product term is A’.

We have B = 0 for this row, so the corresponding literal in the product term is B’.

We have C = 1 for this row, so the corresponding literal in the product term is C.

The product term generated for this row in the truth table is A’·B’·C.

We now address the generation of the canonical POSP form of F1 from the truth table. The
rule is to generate a sum term for each row for which the function value is 0. Reading from
the top of the truth table, the first row of interest is row 1.

A	B	C	F1
0	0	0	0

We have A = 0 for this row, so the corresponding literal in the product term is A.

We have B = 0 for this row, so the corresponding literal in the product term is B.

We have C = 1 for this row, so the corresponding literal in the product term is C.

The product term generated for this row in the truth table is A + B + C.

Thus we have the following representation as Sum of Products

F1 = A’·B’·C + A’·B·C’ + A·B’·C’ + A·B·C
F2 = A’·B·C + A·B’·C + A·B·C’ + A·B·C

We have the following representation as Product of Sums
F1 = (A + B + C)·(A + B’ + C’)·(A’ + B + C’)·(A’ + B’ + C)
F2 = (A + B + C)·(A + B + C’)·(A + B’ + C)·(A’ + B + C)

The choice of representations depends on the number of terms. For N Boolean variables

Let C_SOP be the number of terms in the Sum of Products representation.

Let C_POS be the number of terms in the Product of Sums representation.

Then C_SOP + C_POS = 2^N. In the above example C_SOP = 4 and C_POS = 4, so either choice is
equally good. However, if the Sum of Products representation has 6 terms, then the Product
of Sums representation has only 2 terms, which might recommend it.

Non-Canonical Forms

The basic definition of a canonical form (both SOP and POS) is that every term contain each
variable, either in the negated or non-negated state. In the example above, note that every
product term in the SOP form contains all three variables A, B, and C in some form. The
same holds for the POS forms.

It is often the case that a non-canonical form is simpler. For example, one can easily show
that F2(A, B, C) = A·B + A·C + B·C. Note that in this simplified form, not all variables
appear in each of the terms. Thus, this is a normal SOP form, but not a canonical form.

The simplification can be done by one of three ways: algebraic methods, Karnaugh Maps
(K-Maps), or the Quine-McCluskey procedure. Here we present a simplification of
F2(A, B, C) by the algebraic method with notes to the appropriate postulates and theorems.

The idempotency theorem, states that for any Boolean expression X, we have
X + X = X. Thus X = X + X = X + X + X and A·B·C = A·B·C + A·B·C + A·B·C, as
A·B·C is a valid Boolean expression for any values of A, B, and C.

F2 = A’·B·C + A·B’·C + A·B·C’ + A·B·C Original form
= A’·B·C + A·B’·C + A·B·C’ + A·B·C + A·B·C + A·B·C Idempotence
= A’·B·C + A·B·C + A·B’·C + A·B·C + A·B·C’ + A·B·C Commutativity
= (A’ +A)·B·C + A·(B’ + B)·C + A·B·(C’ + C) Distributivity
= 1·B·C + A·1·C + A·B·1
= B·C + A·C + A·B
= A·B + A·C + B·C Commutativity

The main reason to simplify Boolean expressions is to reduce the number of logic gates
required to implement the expressions. This was very important in the early days of
computer engineering when the gates themselves were costly and prone to failure.
It is less of a concern these days.

More On Conversion Between Truth Tables and Boolean Expressions

We now give a brief discussion on the methods used by this author to derive Boolean
expressions from truth tables and truth tables from canonical form Boolean expressions.
We shall do this be example. Consider the truth table expression for our function F1.

The truth table for F1 is shown below.

Row	A	B	C	F1
0	0	0	0	0
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

The rows for which the function F1 has value 1 are shown in bold font. As noted above, we
can write F1 in the S-list form as F1 = S(1, 2, 4, 7). To convert this form to canonical SOP,
we just replace the decimal numbers by binary; thus F1 = S(001, 010, 100, 111). To work
from the truth tables, we just note the values of A, B, and C in the selected rows.

First write the Boolean expression in a form that cannot be correct, writing one identical
Boolean product term for each of the four rows for which F1 = 1.

F1(A, B, C) = A·B·C + A·B·C + A·B·C + A·B·C

Then write under each term the 0’s and 1’s for the corresponding row.

F1(A, B, C) = A·B·C + A·B·C + A·B·C + A·B·C
0 0 1 0 1 0 1 0 0 1 1 1

Wherever one sees a 0, complement the corresponding variable, to get.

F1(A, B, C) = A’·B’·C + A’·B·C’ + A·B’·C’ + A·B·C

To produce the truth-table from the canonical form SOP expression, just write a 0 under
every complemented variable and a 1 under each variable that is not complemented.

F2(A, B, C) = A’·B·C + A·B’·C + A·B·C’ + A·B·C
0 1 1 1 0 1 1 1 0 1 1 1

This function can be written as F2 = S(011, 101, 110, 111) in binary or F2 = S(3, 5, 6, 7).
To create the truth table for this, just make 8 rows and fill rows 3, 5, 6, and 7 with 1’s and
the other rows with 0’s.

It is also possible to generate the canonical POS expressions using a similar procedure.
Consider again the truth table for F1, this time with the rows with 0 values highlighted.

Row	A	B	C	F1
0	0	0	0	0
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

The rows for which the function F1 has value 0 are shown in bold font. As noted above, we
can write F1 in the P-list form as F1 = P(0, 3, 5, 6). To convert this form to canonical POS,
we just replace the decimal numbers by binary; thus F1 = P(000, 011, 101, 110). To work
from the truth tables, we just note the values of A, B, and C in the selected rows.

Again we write a Boolean expression with one sum term for each of the four rows for
which the function has value 0. At the start, this is not correct.

F1 = (A + B + C) · (A + B + C) · (A + B + C) · (A + B + C)

Now write the expression with 0’s and 1’s for the corresponding row numbers.

F1 = (A + B + C) · (A + B + C) · (A + B + C) · (A + B + C)
0 0 0 0 1 1 1 0 1 1 1 0

Wherever one sees a 1, complement the corresponding variable, to get.

F1 = (A + B + C)·(A + B’ + C’)·(A’ + B + C’)·(A’ + B’ + C)

To produce the truth-table from the canonical form POS expression, just write a 1 under
every complemented variable and a 0 under each variable that is not complemented.

F2 = (A + B + C)·(A + B + C’)·(A + B’ + C)·(A’ + B + C)

0 0 0 0 0 1 0 1 0 1 0 0

This function can be written as F2 = P(000, 001, 010, 100) in binary or F2 = P(0, 1, 2, 4).
To create the truth table for this, just make 8 rows and fill rows 0, 1, 2, and 4 with 0’s and
the other rows with 1’s.

Implementation of Boolean Logic by Circuitry

Having worn ourselves out on the algebraic view of Boolean functions, we now return to the
fact that these functions must be implemented in hardware if a digital computer is to be built.
This section presents the circuits used to implement basic Boolean functions.

The Boolean values are represented by specific voltages in the electronic circuitry. As a
result of experience, it has been found desirable only to have two voltage levels, called High
and Low or H and L. This leads to two types of logic

Negative Logic High = 0 Low = 1

Positive Logic High = 1 Low = 0

This course will focus on Positive Logic and ignore Negative Logic. As a matter of fact, we
shall only occasionally concern ourselves with voltage levels. In Positive Logic, +5 volts is
taken as the high level and 0 volts as the low level. These are the ideals. In actual practice,
the standards allow some variation depending on whether the level is output or input.

Output of Logic Gate Input to Logic Gate

Logic High 2.4 – 5.0 volts 2.0 – 5.0 volts

Logic Low 0.0 – 0.4 volts 0.0 – 0.8 volts

The tighter constraints on output allow for voltage degradation due to the practicalities of
implementing electrical circuits. One of these practicalities is called fan-out, used to denote
the maximum number of gates that can be attached to the output of one specific gate. This
relates to the maximum amount of current that a given gate can produce. The fan-out
problem is illustrated in everyday life when one sees the lights dim as a new appliance, such
as an electric furnace, turns on. There is also an easily-observed hydraulic equivalent to the
limited fan-out problem: wait until someone is in the shower and then flush every commode
in the house. The water main pipe can only supply so much cold water so that the pressure
to the shower will drop, often with hilarious consequences.

Basic Gates for Boolean Functions

We now discuss a number of basic logic gates used to implement Boolean functions. The
gates of interest at this point are AND, OR, NOT, NAND (NOT AND), NOR (NOT OR) and
XOR (Exclusive OR). The Exclusive OR gate is the same as the OR gate except that the
output is 0 (False) when both inputs are 1 (True). The symbol for XOR is Å.

The first gate to be discussed is the OR gate. The truth table for a two-input OR gate is
shown below. In general, if any input to an OR gate is 1, the output is 1.

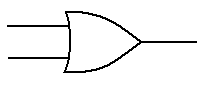A B A + B

0 0 0

0 1 1

1 0 1

1 1 1

The next gate to be discussed is the AND gate. The truth table for a two-input AND gate is
shown now. In general, if any input to an AND gate is 0, the output is 0.

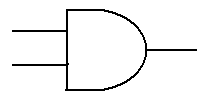A B A · B

0 0 0

0 1 0

1 0 0

1 1 1

The third of the four basic gates is the single input NOT gate. Note that there are two ways
of denoting the NOT function. NOT(A) is denoted as either A’ or . We use as often as
possible to represent NOT(A), but may become lazy and use the other notation.

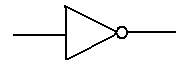
A

0 1

1 0

The last of the gates to be discussed at this first stage is not strictly a basic gate. We include
it at this level because it is extremely convenient. This is the two-input Exclusive OR (XOR)
gate, the function of which is shown in the following truth table.

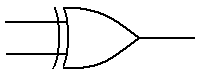A B A Å B

0 0 0

0 1 1

1 0 1

1 1 0

We note immediately an interesting and very useful connection between the XOR function
and the NOT function. For any A, A Å 0 = A, and A Å 1 =. The proof is by truth table.

A B A Å B Result

0 0 0 A

1 0 1 A This result is extremely useful when designing

0 1 1 a ripple carry adder/subtractor.

1 1 0

The basic logic gates are defined in terms of the binary Boolean functions. Thus, the basic
logic gates are two-input AND gates, two-input OR gates, NOT gates, two-input NAND
gates, two-input NOR gates, and two-input XOR gates.

It is common to find three-input and four-input varieties of AND, OR, NAND, and NOR
gates. The XOR gate is essentially a two-input gate; three input XOR gates may exist but
they are hard to understand.

Consider a four input AND gate. The output function is described as an easy generalization
of the two input AND gate; the output is 1 (True) if and only if all of the inputs are 1,
otherwise the output is 0. One can synthesize a four-input AND gate from three two-input
AND gates or easily convert a four-input AND gate into a two-input AND gate. The student
should realize that each figure below represents only one of several good implementations.

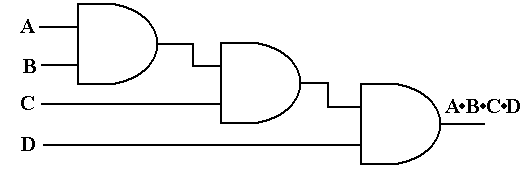
Figure: Three 2-Input AND Gates Make a 4-Input AND Gate

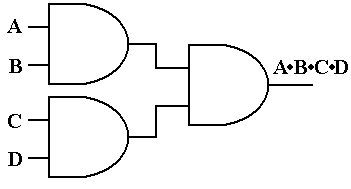
Figure: Another Way to Configure Three 2-Input AND Gates as a 4-Input AND Gate

Figure: Two Ways to Configure a 4-Input AND Gate as a 2-Input AND Gate

Here is the general rule for N-Input AND gates and N-Input OR gates.

AND Output is 0 if any input is 0. Output is 1 only if all inputs are 1.
OR Output is 1 if any input is 1. Output is 0 only if all inputs are 0.

XOR For N > 2, N-input XOR gates are not useful and will be avoided.

“Derived Gates”

We now show 2 gates that may be considered as derived from the above: NAND and NOR.

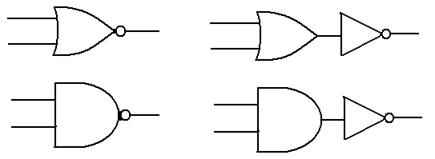The NOR gate is the
same as an OR gate
followed by a NOT
gate.

The NAND gate is the
same as an AND gate
followed by a NOT
gate.

Electrical engineers may validly object that these two gates are not “derived” in the sense
that they are less basic than the gates previously discussed. In fact, NAND gates are often
used to make AND gates. As always, we are interested in the non-engineering approach and
stay with our view: NOT, AND, and OR are basic. We shall ignore the XNOR gate and, if
needed, implement its functionality by an XOR gate followed by a NOT gate.

As an exercise in logic, we show that the NAND (Not AND) gate is fundamental in that it
can be used to synthesize the AND, OR, and NOT gates. We begin with the basic NAND.

The basic truth table for the NAND is given by

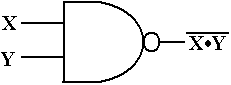X Y X·Y

0 0 0 1

0 1 0 1

1 0 0 1

1 1 1 0

From this truth table, we see that = 1 and = 0, so we conclude that =
and immediately have the realization of the NAND gate as a NOT gate.

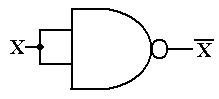
Figure: A NAND Gate Used as a NOT Gate

To synthesize an AND gate from a NAND gate, we just note that NOT NAND is the same as
NOT NOT AND, which is the same as AND. In other words = X · Y, and we follow
the NAND gate with the NOT gate, implemented from another NAND gate.

Here is the AND gate as implemented from two NAND gates.

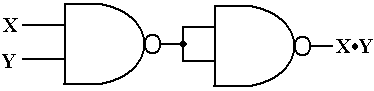
Figure: Two NAND Gates to Make an AND Gate

In order to implement an OR gate, we must make use of DeMorgan’s law. As stated above,
DeMorgan’s law is usually given as = + . We use straightforward algebraic
manipulation to arrive at a variant statement of DeMorgan’s law.

= = X + Y

Using this strange equality, a direct result of DeMorgan’s law, we have the OR circuit.

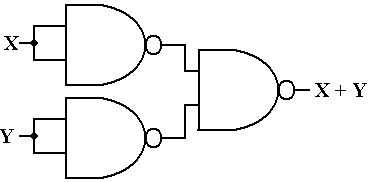
Figure: Three NAND Gates Used to Make an OR Gate

Circuits and Truth Tables

We now address an obvious problem – how to relate circuits to Boolean expressions.
The best way to do this is to work some examples. Here is the first one.

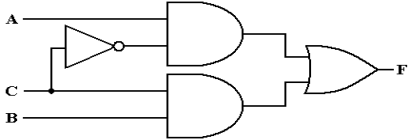
Question:

What are the truth table and the Boolean expressions that describe the following circuit?

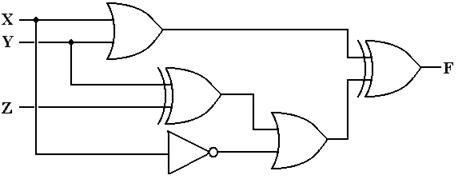
The method to get the answer is to label each gate and determine the output of each. The
following diagram shows the gates as labeled and the output of each gate.

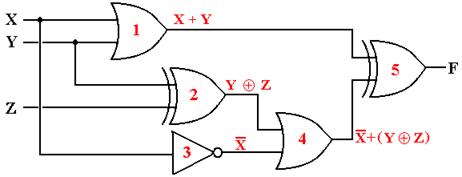
The outputs of each gate are as follows:
The output of gate 1 is (X + Y),
The output of gate 2 is (Y Å Z),
The output of gate 3 is X’,
The output of gate 4 is X’ + (Y Å Z), and
The output of gate 5 is (X + Y) Å [X’ + (Y Å Z)]

We now produce the truth table for the function.

X	Y	Z	X + Y	(Y Å Z)	X’	X’ + (Y Å Z)	(X + Y) Å [X’+(Y Å Z)]
0	0	0	0	0	1	1	1
0	0	10	0	1	1	1	1
0	1	0	1	1	1	1	0
0	1	1	1	0	1	1	0
1	0	0	1	0	0	0	1
1	0	1	1	1	0	1	0
1	1	0	1	1	0	1	0
1	1	1	1	0	0	0	1

The above is the truth table for the function realized by the figure on the previous page.

Lets give a simpler representation.

X	Y	Z	F(X, Y, Z)
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

We now produce both the SOP and POS representations of this function. For the SOP,
we look at the four 1’s of the function; for the POS, we look at the four zeroes.

SOP

F(X, Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X·Y’·Z’ + X·Y·Z
0 0 0 0 0 1 1 0 0 1 1 1

POS

F(X, Y, Z) = (X + Y’ + Z) · (X + Y’ + Z’) · (X’ + Y + Z’) · (X’ + Y’ + Z)
0 1 0 0 1 1 1 0 1 1 1 0

To simplify in SOP, we write the function in a slightly more complex form.
F(X, Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X’·Y’·Z’ + X·Y’·Z’ + X·Y·Z
= X’·Y’·(Z’ + Z) + (X + X’)·Y’·Z’ + X·Y·Z
= X’·Y’ + Y’·Z’ + X·Y·Z

To simplify in POS, we again write the function in a slightly bizarre form.
F(X, Y, Z) = (X + Y’ + Z) · (X + Y’ + Z’) · (X’ + Y + Z’)
· (X’ + Y’ + Z) · (X + Y’ + Z)
= (X + Y’) · (X’ + Y + Z’)· (Y’ + Z)

We close this discussion by presenting the canonical SOP and POS using another notation.

We rewrite the truth table for F(X, Y, Z), adding row numbers.

	X	Y	Z	F(X, Y, Z)
0	0	0	0	1
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

Noting the positions of the 1’s and 0’s in the truth table gives us our standard notation.

F(X, Y, Z) = S(0, 1, 4, 7)

F(X, Y, Z) = P(2, 3, 5, 6)

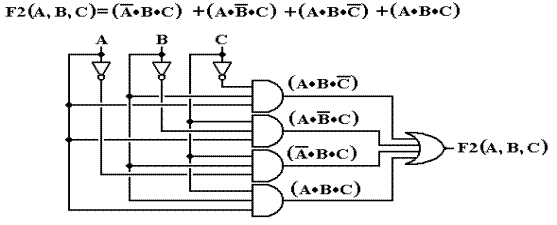
Question:
What is the circuit that corresponds to the following two Boolean functions?

The reader might note that the two are simply different representations of the same function.

The answer here is just to draw the circuits. The general rule is simple.
SOP One OR gate connecting the output of a number of AND gates.
POS One AND gate connecting the output of a number of OR gates.

Here is the circuit for F2(A, B, C). It can be simplified.

Here is the circuit for G2(A, B, C). It can be simplified.

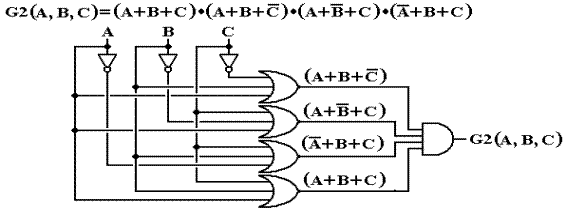
The Non–Inverting Buffer
We now investigate a number of circuit elements that do not directly implement Boolean
functions. The first is the non–inverting buffer, which is denoted by the following symbol.

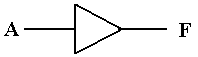
Logically, a buffer does nothing. Electrically, the buffer serves as an amplifier converting a
degraded signal into a more useable form; specifically it does the following.

A logic 1 (voltage in the range 2.0 – 5.0 volts) will be output as 5.0 volts.
A logic 0 (voltage in the range 0.0 – 0.8 volts) will be output as 0.0 volts.

While one might consider this as an amplifier, it is better considered as a “voltage adjuster”. We shall see another use of this and similar circuits when we consider MSI (Medium Scale Integrated) circuits in a future chapter.

More “Unusual” Circuits

Up to this point, we have been mostly considering logic gates in their ability to implement
the functions of Boolean algebra. We now turn our attention to a few circuits that depend as
much on the electrical properties of the basic gates as the Boolean functions they implement.
We begin with a fundamental property of all electronic gates, called “gate delay”.
This property will become significant when we consider flip–flops.

We begin with consideration of a simple NOT gate, with Y = , as shown below.

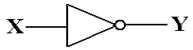
From the viewpoint of Boolean algebra, there is nothing special about this gate. It
implements the Boolean NOT function; nothing else. From the viewpoint of actual
electronic circuits, we have another issue. This issue, called “gate delay”, reflects the fact
that the output of a gate does not change instantaneously when the input changes. The output
always lags the input by an interval of time that is the gate delay. For standard TTL circuits,
such as the 74LS04 that implements the NOT function, the gate delay is about ten
nanoseconds; the output does not change until 10 nanoseconds after the input changes.

In the next figure, we postulate a NOT gate with a gate delay of 10 nanoseconds with an
input pulse of width 20 nanoseconds. Note that the output trails the input by the gate delay;
in particular we have an interval of 10 nanoseconds (one gate delay) during which X = 1 and
= 1, and also an interval of 10 nanoseconds during which X = 0 and = 0. This is not a
fault of the circuit; it is just a well–understood physical reality.

The table just below gives a list of gate delay times for some popular gates. The source of
this is the web page http://www.cs.uiowa.edu/~jones/logicsim/man/node5.html

Number	Description	Gate Delay in Nanoseconds
74LS00	2–Input NAND	9.5
74LS02	2–Input NOR	10.0
74LS04	Inverter (NOT)	9.5
74LS08	2–Input AND	9.5
74LS32	2–Input OR	14.0
74LS86	2–Input XOR	10.0

We can see that there is some variation is the gate delay times for various basic logic gates,
but that the numbers tend to be about 10.0 nanoseconds. In our discussions that follow we
shall make the assumption that all logic gates display the same delay time, which we shall
call a “gate delay”. While we should understand that this time value is about
10 nanoseconds, we shall not rely on its precise value.

There are a number of designs that call for introducing a fixed delay in signal propagation so
that the signal does not reach its source too soon. This has to do with synchronization issues
seen in asynchronous circuits. We shall not study these, but just note them.

The most straightforward delay circuit is based on the Boolean identity.

This simple Boolean identity leads to the delay circuit.

The delay is shown in the timing diagram below, in which Z lags X by 20 nanoseconds.

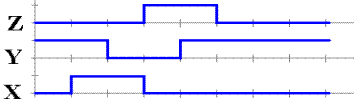
The rule for application of gate delays is stated simply below.

The output of a gate is stable one gate delay after all of its inputs are stable.

We should note that the delay circuit above is logically equivalent to the non–inverting buffer
discussed just above. The non–inverting buffer is different in two major ways: its time delay
is less, and it usually serves a different purpose in the design.

It should be clear that the output of a gate changes one gate delay after any of its inputs
change. To elaborate on this statement, let us consider an exclusive or (XOR) chip. The
truth table for an XOR gate is shown in the following table.

X	Y	X Å Y
0	0	0
0	1	1
1	0	1
1	1	0

We now examine a timing diagram for this circuit under the assumption that the inputs are
initially both X = 0 and Y = 0. First X changes to 1 and some time later so does Y.

Here is the circuit.

Here is the timing diagram.

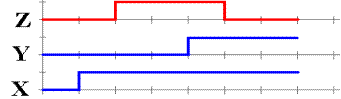
Note that the output, Z, changes one gate delay after input X changes and again one gate
delay after input Y changes. This unusual diagram is shown only to make the point that the
output changes one gate delay after any change of input. In the more common cases, all
inputs to a circuit change at about the same time, so that this issue does not arise.

We now come to a very important circuit, one that seems to implement a very simple
Boolean identity. Specifically, we know that for all Boolean variables X:

Given the above identity, the output of the following circuit would be expected to be
identically 0. Such a consideration does not account for gate delays.

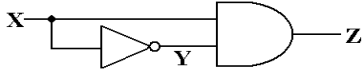
Suppose that input X goes high and stays high for some time, possibly a number of gate
delays. The output Z is based on the fact that the output Y lags X by one gate delay.

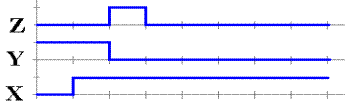
Suppose we are dealing with the typical value of 10 nanoseconds for a gate delay.

At T = 10, the value of X changes. Neither Y nor Z changes.

At T = 20, the values of each of Y and Z change.

The value of Y reflects the value of X at T = 10, so Y becomes 0.
The value of Z reflects the value of both X and Y at T = 10.
At T = 10, we had both X = 1 and Y = 1, so Z becomes 1 at T = 20.

At T = 30, the value of Z changes again to reflect the values of X and Y at T = 20.
Z becomes 0.

What we have in the above circuit is a design to produce a very short pulse, of time duration
equal to one gate delay. This facility will become very useful when we begin to design
edge–triggered flip–flops in a future chapter.

Tri–State Buffers

We have now seen all of the logic gates to be used in this course. There is one more gate
type that needs to be examined – the tri-state buffer. We begin with the examination of a
simple (non-inverting buffer) and comment on its function. We discuss two basic types:
enabled–high and enabled–low. The circuit diagrams for these are shown below.

The difference between these two circuits relates to how the circuits are enabled. Note that
the enabled-low tri–state buffer shows the standard use of the NOT dot on input.

The following figure shows two ways of implementing an Enabled–Low Tri-State buffer,
one using an Enabled-High Tri-State with a NOT gate on the Enable line. The significance
of the overbar on the Enable input is that the gate is active when the control is logic 0.

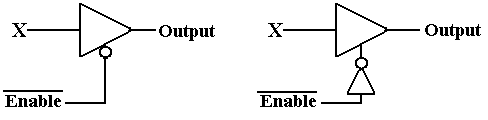
Figure: Two Views of an Enabled-Low Tri-State Buffer

A tri-state buffer acts as a simple buffer when it is enabled; it passes the input through while
adjusting its voltage to be closer to the standard. When the tri-state buffer is not enabled, it
acts as a break in the circuit or an open switch (if you understand the terminology). A gate
may be enabled high (C = 1) or enabled low (C = 0). Consider an enabled–high tri-state.

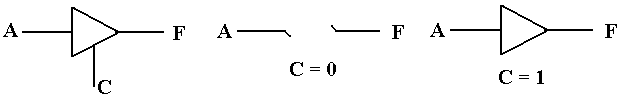
Figure: Circuits Equivalent to an Enabled Tri–State and a Disabled Tri-State

When the enable signal is C = 1, the tri-state acts as a simple buffer and asserts its input as an
output. When the enable signal is C = 0, the tri-state does not assert anything on the output.

Another way to describe a tri–state buffer is to say that it is in a high-impedance state (often
called a “high–Z state” by engineers who use the symbol “Z” for impedance) when it is not
enabled. This is simply to say that it offers such a resistance to transmission of its input that
for all practical purposed it does not assert anything on its output.

The Third State

The definition of this “third state” in a tri–state buffer is both obvious and subtle. Compare
the two circuits in the figure below. One is a buffer; the other is a tri–state buffer.

For the circuit on the left, either F = 0 (0 volts) or F = 1 (5 volts). There is no other option.
For the circuit on the right, when C = 1 then F = A, and takes a value of either 0 volts or 5
volts, depending on the value of the input. When C = 0, F is simply not defined.

One of the better ways to understand the tri-state buffer is to consider the following circuit
with two Boolean inputs A and B, one output F, and an enable signal C.

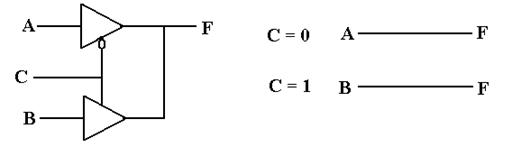
Note that the two tri–state buffers are enabled differently, so that the top buffer is enabled if
and only if the bottom buffer is not enabled, and vice versa. The design insures that at no
time are both of the tri–state buffers enabled, so that there is no conflict of voltages.

C = 0 Only the top buffer is enabled F = A
C = 1 Only the bottom buffer is enabled F = B

The reader will note that the above circuit is logically equivalent to the one that follows.

Given only this simple example, one might reasonably question the utility of tri–state buffers.
It appears that they offer a novel and complex solution to a simple problem. The real use of
these buffers lies in placing additional devices on a common bus, a situation in which the use
of larger OR gates might prove difficult.

Before addressing the standard uses of the tri–state buffer, we must review some of the basics
of direct current electricity: voltage, current, and resistance.

Review of Basic Electronics

A traditional presentation of this material might have begun with a review of the basic
concepts of direct current electricity. Your author has elected to postpone that discussion
until this point in the course, at which time it is needed.

A Basic Circuit

We begin our discussion with a simple example circuit – a flashlight (or “electric torch” as
the Brits call it). This has three basic components: a battery, a switch, and a light bulb. For
our purpose, the flashlight has two possible states: on and off. Here are two diagrams.

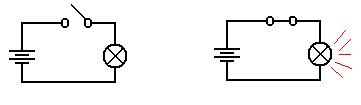
Light is Off Light is On

In the both figures, we see a light bulb connected to a battery via two wires and a switch.
When the switch is open, it does not allow electricity to pass and the light is not illuminated.
When the switch is closed, the electronic circuit is completed and the light is illuminated.

The figure above uses a few of the following basic circuit elements.

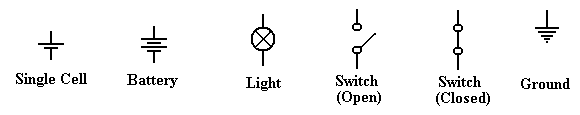
We now describe each of these elements and then return to our flashlight example. The first
thing we should do is be purists and note the difference between a cell and a battery, although
the distinction is quite irrelevant to this course. A cell is what one buys in the stores today
and calls a battery; these come in various sizes, including AA, AAA, C, and D. Each of
these cells is rated at 1.5 volts, due to a common technical basis for their manufacture.
Strictly speaking, a battery is a collection of cells, so that a typical flashlight contains one
battery that comprises two cells; usually AA, C, or D. An automobile battery is truly a
battery, being built from a number of lead-acid cells.

A light is a device that converts electronic current into visible light. This is not a surprise.
A switch is a mechanical device that is either open (not allowing transmission of current) or
closed (allowing the circuit to be completed). Note that it is the opposite of a door, which
allows one to pass only when open.

The Idea of Ground

Consider the above circuit, which suggests a two-wire design: one wire from the battery to
the switch and then to the light bulb, and another wire from the bulb directly to the battery.
One should note that the circuit does not require two physical wires, only two distinct paths
for conducting electricity. Consider the following possibility, in which the flashlight has a
metallic case that also conducts electricity.

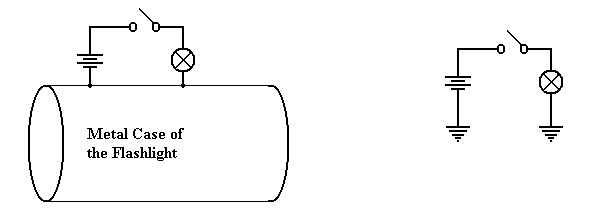
Physical Connection Equivalent Circuit

Consider the circuit at left, which shows the physical connection postulated. When the
switch is open, no current flows. When the switch is closed, current flows from the battery
through the switch and light bulb, to the metallic case of the flashlight, which serves as a
return conduit to the battery. Even if the metallic case is not a very good conductor, there
is much more of it and it will complete the circuit with no problem.

In electrical terms, the case of the battery is considered as a common ground, so that the
equivalent circuit is shown at right. Note the new symbol in this circuit – this is the ground
element. One can consider all ground elements to be connected by a wire, thus completing
the circuit. In early days of radio, the ground was the metallic case of the radio – an
excellent conductor of electricity. Modern automobiles use the metallic body of the car itself
as the ground. Although iron and steel are not excellent conductors of electricity, the sheer
size of the car body allows for the electricity to flow easily.

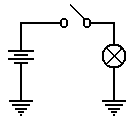
To conclude, the circuit at left will be our representation of a
flashlight. The battery provides the electricity, which flows through
the switch when the switch is closed, then through the light bulb, and
finally to the ground through which it returns to the battery.

As a convention, all switches in diagrams will be shown in the open
position unless there is a good reason not to.

The student should regard the above diagram as showing a switch which is not necessarily
open, but which might be closed in order to allow the flow of electricity. The convention of
drawing a switch in the open position is due to the fact that it is easier to spot in a diagram.

Voltage, Current, and Resistance
It is now time to become a bit more precise in our discussion of electricity. We need to
introduce a number of basic terms, many of which are named by analogy to flowing water.
The first term to define is current, usually denoted in equations by the symbol I. We all
have an intuitive idea of what a current is. Imagine standing on the bank of a river and
watching the water flow. The faster the flow of water, the greater the current; flows of water
are often called currents.

In the electrical terms, current is the flow of electrons, which are one of the basic building
blocks of atoms. While electrons are not the only basic particles that have charge, and are
not the only particle that can bear a current; they are the most common within the context of
electronic digital computers. Were one interested in electro-chemistry he or she might be
more interested in the flow of positively charged ions.

All particles have one of three basic electronic charges: positive, negative, or neutral. Within
an atom, the proton has the positive charge, the electron has the negative charge, and the
neutron has no charge. In normal life, we do not see the interior of atoms, so our experience
with charges relates to electrons and ions. A neutral atom is one that has the same number of
protons as it has electrons. However, electrons can be quite mobile, so that an atom may gain
or lose electrons and, as a result, have too many electrons (becoming a negative ion) or too
few electrons (becoming a positive ion). For the purposes of this course, we watch only the
electrons and ignore the ions.

An electric charge, usually denoted by the symbol Q, is usually associated with a large
number of electrons that are in excess of the number of positive ions available to balance
them. The only way that an excess of electrons can be created is to move the electrons from
one region to another – robbing one region of electrons in order to give them to another.
This is exactly what a battery does – it is an electron “pump” that moves electrons from the
positive terminal to the negative terminal. Absent any “pumping”, the electrons in the
negative terminal would return to the positive region, which is deficient in electrons, and
cause everything to become neutral. But the pumping action of the battery prevents that.
Should one provide a conductive pathway between the positive and negative terminals of a
battery, the electrons will flow along that pathway, forming an electronic current.

To clarify the above description, we present the following diagram, which shows a battery, a
light bulb, and a closed switch. We see that the flow of electrons within the battery is only a
part of a larger, complete circuit.

Materials are often classified by their abilities to conduct electricity. Here are two common
types of materials.

Conductor A conductor is a substance, such as copper or silver, through which
electrons can flow fairly easily.

Insulator An insulator is a substance, such as glass or wood, that offers
significant resistance to the flow of electrons. In many of our
circuit diagrams we assume that insulators do not transmit electricity
at all, although they all do with some resistance.

The voltage is amount of pressure in the voltage pump. It is quite
similar to water pressure in that it is the pressure on the electrons that
causes them to move through a conductor. Consider again our
flashlight example. The battery provides a pressure on the electrons
to cause them to flow through the circuit. When the switch is open,
the flow is blocked and the electrons do not move. When the switch
is closed, the electrons move in response to this pressure (voltage)
and flow through the light bulb. The light bulb offers a specific
resistance to these electrons; it heats up and glows.

As mentioned above, different materials offer various abilities to transmit electric currents.
We have a term that measures the degree to which a material opposes the flow of electrons;
this is called resistance, denoted by R in most work. Conductors have low resistance (often
approaching 0), while insulators have high resistance. In resistors, the opposition to the flow
of electrons generates heat – this is the energy lost by the electrons as they flow through the
resistor. In a light bulb, this heat causes the filament to become red hot and emit light.

An open switch can be considered as a circuit element of extremely high resistance.

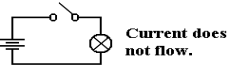
Summary
We have discussed four terms so far. We now should mention them again.

Charge This refers to an unbalanced collection of electrons. The term used
for denoting charge is Q. The unit of charge is a coulomb.

Current This refers to the rate at which a charge flows through a conductor.
The term used for denoting current is I. The unit of current is an ampere.
Voltage This refers to a force on the electrons that causes them to move. This force
can be due to a number of causes – electro-chemical reactions in batteries
and changing magnetic fields in generators. The term used for denoting
voltage is V or E (for Electromotive Force). The unit of current is a volt.

Resistance This is a measure of the degree to which a substance opposes the flow of
electrons. The term for resistance is R. The unit of resistance is an ohm.

Ohm’s Law and the Power Law
One way of stating Ohm’s law (named for Georg Simon Ohm, a German teacher who
discovered the law in 1827) is verbally as follows.

The current that flows through a circuit element is directly proportional to the
voltage across the circuit element and inversely proportional to the resistance
of that circuit element.

What that says is that doubling the voltage across a circuit element doubles the current flow
through the element, while doubling the resistance of the element halves the current.

Let’s look again at our flashlight example, this time with the switch shown as closed.

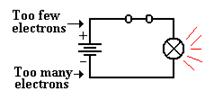
The chemistry of the battery is pushing electrons away
from the positive terminal, denoted as “+” through the
battery towards the negative terminal, denoted as “–“.

This causes a voltage across the only resistive element
in the circuit – the light bulb. This voltage placed across the light bulb causes current to
flow through it.

In algebraic terms, Ohm’s law is easily stated: E = I·R, where
E is the voltage across the circuit element,
I is the current through the circuit element, and
R is the resistance of the circuit element.

Suppose that the light bulb has a resistance of 240 ohms and has a voltage of 120 volts
across it. Then we say E = I·R or 120 = I·240 to get I = 0.5 amperes.

As noted above, an element resisting the flow of electrons absorbs energy from the flow it
obstructs and must emit that energy in some other form. Power is the measure of the flow of
energy. The power due to a resisting circuit element can easily be calculated.

The power law is states as P = E·I, where
P is the power emitted by the circuit element, measured in watts,
E is the voltage across the circuit element, and
I is the current through the circuit element.

Thus a light bulb with a resistance of 240 ohms and a voltage of 120 volts across it has
a current of 0.5 amperes and a power of 0.5 · 120 = 60 watts.

There are a number of variants of the power law, based on substitutions from Ohm’s law.
Here are the three variants commonly seen.

P = E·I P = E² / R P = I²·R

In our above example, we note that a voltage of 120 volts across a resistance of 60 ohms
would produce a power of P = (120)² / 240 = 14400 / 240 = 60 watts, as expected.

The alert student will notice that the above power examples were based on AC circuit
elements, for which the idea of resistance and the associated power laws become more
complex (literally). Except for a few cautionary notes, this course will completely ignore
the complexities of alternating current circuits.

Resistors in Series
There are very many interesting combinations of resistors found
in circuits, but here we focus on only one – resistors in series;
that is one resistor placed after another. In this figure, we
introduce the symbol for a resistor.

Consider the circuit at right, with two resistors having
resistances of R₁ and R₂, respectively. One of the basic laws of
electronics states that the resistance of the two in series is
simply the sum: thus R = R₁ + R₂. Let E be the voltage provided by the battery. Then the
voltage across the pair of resistors is given by E, and the current through the circuit elements
is given by Ohm’s law as I = E / (R₁ + R₂). Note that we invoke another fundamental law
that the current through the two circuit elements in series must be the same.

Again applying Ohm’s law we can obtain the voltage drops across each of the two resistors.
Let E₁ be the voltage drop across R₁ and E₂ be that across R₂. Then

E₁ = I·R₁ = R₁·E / (R₁ + R₂), and
E₂ = I·R₂ = R₂·E / (R₁ + R₂).
It should come as no surprise that E₁ + E₂ = R₁·E / (R₁ + R₂) + R₂·E / (R₁ + R₂)
= (R₁ + R₂)·E / (R₁ + R₂) = E.

If, as is commonly done, we assign the ground state as having zero voltage, then the voltages
at the two points in the circuit above are simple.

1) At point 1, the voltage is E, the full voltage of the battery.
2) At point 2, the voltage is E₂ = I·R₂ = R₂·E / (R₁ + R₂).

Before we present the significance of the above circuit, consider two special cases.

In the circuit at left, the second resistor is replaced by a conductor having zero resistance.
The voltage at point 2 is then E₂ = 0·E / (R₁ + 0) = 0. As point 2 is directly connected to
ground, we would expect it to be at zero voltage.

Suppose that R₂ is much bigger than R₁. Let R₁ = R and R₂ = 1000·R. We calculate the
voltage at point 2 as E₂ = R₂·E / (R₁ + R₂) = 1000·R·E / (R + 1000·R) = 1000·E/1001, or
approximately E₂ = (1 – 1/1000)·E = 0.999·E. Point 2 is essentially at full voltage.

Putting a Resistor and Switch in Series
We now consider an important circuit that is related to the above circuit. In this circuit the
second resistor, R₂, is replaced by a switch that can be either open or closed.

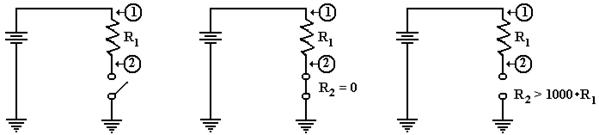
The Circuit Switch Closed Switch Open

The circuit of interest is shown in the figure at left. What we want to know is the voltage at
point 2 in the case that the switch is closed and in the case that the switch is open. In both
cases the voltage at point 1 is the full voltage of the battery.

When the switch is closed, it becomes a resistor with no resistance; hence R₂ = 0. As we
noted above, this causes the voltage at point 2 to be equal to zero.

When the switch is open, it becomes equivalent to a very large resistor. Some say that the
resistance of an open switch is infinite, as there is no path for the current to flow. For our
purposes, it suffices to use the more precise idea that the resistance is very big, at least 1000
times the resistance of the first resistor, R₁. The voltage at point 2 is the full battery voltage.

Before we present our circuit, we introduce a notation used in
drawing two wires that appear to cross. If a big dot is used at
the crossing, the two wires are connected. If there is a gap, as in vthe right figure, then the wires do not connect.

Here is a version of the circuit as we shall use it later.

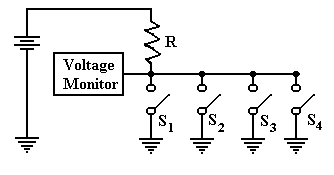
In this circuit, there are four switches attached to the wire. The voltage is monitored by
another circuit that is not important at this time. If all four switches are open, then the
voltage monitor registers full voltage. If one or more of the switches is closed, the monitor
registers zero voltage. This is the best way to monitor a set of switches.

Back to Tri–State Buffers
We use the above verbiage to present a new view of tri–state buffers. Consider the following
two circuits, which have been used previously in this chapter. Suppose that the battery is
rated at five volts. In the circuit at left, point A is at 5 volts and point B is at 0 volts. In the
circuit at right, point B is clearly at 0 volts, but the status of point A is less clear.

What is obvious about the circuit at right is that there is no current flowing through it and no
power being emitted by the light bulb. For this reason, we often say that point A is at 0 volts,
but it is better to say that there is no specified voltage at that point. This is equivalent to the
third state of a tri–state buffer; the open switch is not asserting anything at point A.

Perhaps the major difference between the two circuits is that we can add another battery to
the circuit at right and define a different voltage at point A. As long as the switch remains
open, we have no conflict. Were the switch to be closed, we would have two circuits trying
to force a voltage at point A. This could lead to a conflict.

Device Polling
Here is a more common use of tri–state buffers. Suppose a number of devices, each of which
can signal a central voltage monitor by asserting logic zero (0 volts) on a line. Recalling that
a logic AND outputs 0 if any of its inputs are 0, we could implement the circuit as follows.

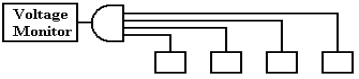
Suppose we wanted to add another device. This would require pulling the 4–input AND gate
and replacing it with a 5–input AND gate. Continual addition of devices would push the
technology beyond the number of inputs a normal gate will support.

The tri–state solution avoids these problems. This circuit repeats the one shown above with
the switches replaced by tri–state buffers, which should be viewed as switches.

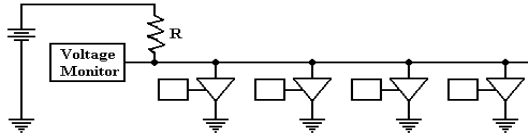
One should note that additional devices can be added to this circuit merely by attaching
another tri–state switch. The only limit to extensibility of this circuit arises from timing
considerations of signal propagation along the shared line.

Analysis of the Four–Tristate Circuit

In order to analyze the circuit at the bottom of the previous page, we refer back to the circuit
on the page before that. We need to understand the voltage at the monitor, which is assumed
to be the input to a digital gate in the control logic of the CPU. While a precise discussion of
this circuit involves treating resistors in parallel, such is not needed to be accurate here.

First, assume that none of the tri–states are enabled. In that case, the circuit is equivalent to
the one in the next figure.

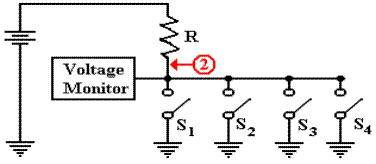
The voltage at point 2 is the full
battery voltage, as the resistance
between that point and ground is
essentially infinite.

E₂ = E / (1 + R₁/R₂)
E₂ » E · (1 – R₁/R₂),
but R₁/R₂ » 0.

Now consider the situation in which one of the tri–state buffers is enabled. Tri–state 2 has
been chosen arbitrarily.

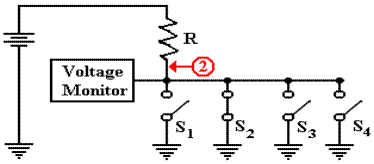
Now there is a direct path of zero
resistance between point 2 and
ground. The voltage at that point
drops to 0, with the entire
voltage drop being across
the resistor R.

Finally consider the situation in which more than one of the tri–state buffers is enabled.
As before, the choice is arbitrary.

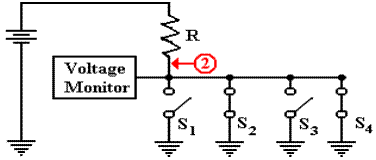Again, there is a direct path of
zero resistance between point 2
and ground. The fact that there
are two such paths has no
practical consequences. The
only criterion is one or more
path of zero resistance.

Solved Problems

We now present a series of solved problems from previous homework and exams.

1. Draw a circuit diagram to show how to implement
a) a three-input AND gate using only two-input AND gates.
b) a four-input AND gate using only three-input AND gates.
c) a three-input AND gate using only one four-input AND gate.

One set of solutions is shown below. There are others.

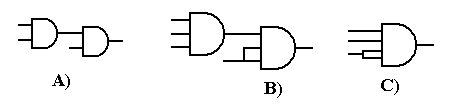
2 If A = 0, B = 1, C = 0, and D = 1, find the value of F for each of the following.

a) F = A·B’ + C
Answer: F = 0·1’ + 0 = 0·0 + 0 = 0
b) F = A·B’ + C’·D + C·D
Answer: F = 0·1’ + 0’·1 + 0·1 = 0·0 + 1·1 + 0·1 = 0 + 1 + 0 = 1
c) F = (A + B’)·(C’ + A)·(A + B·C)

Answer: F = (0 + 1’)·(0’ + 0)·(0 + 1·0) = (0 + 0)·(1 + 0)·(0 + 0) = 0·1·0 = 0

3 Consider the exclusive OR expression, denoted by the symbol Å.
a) Produce a truth-table for the expression XÅYÅZ, evaluated as X Å [Y Å Z].
b) Give the equivalent canonical SOP expression for this function.

ANSWER: Here is the truth table.

X	Y	Z	Y Å Z	X Å [Y Å Z]
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	0	1

We have seen this one many times before. F(X, Y, Z) = S(1, 2, 4, 7)

4 Draw a circuit diagram to show how to implement a three-input NAND
gate using only two-input NAND gates. This is not an easy problem.

ANSWER: The best way to attack this problem is to use truth tables as a starting point.

We begin with the truth table for the two–input NAND.

A	B	A·B	NAND
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

Just to be complete, let’s extend this to the truth table for the desired 3–input NAND gate.

A	B	C	A·B·C	NAND
0	0	0	0	1
0	0	1	0	1
0	1	0	0	1
0	1	1	0	1
1	0	0	0	1
1	0	1	0	1
1	1	0	0	1
1	1	1	1	0

The answer will become a bit easier to see if we change a column and rearrange the table.

A	B	C	NAND(A, B)	NAND(A, B, C)
0	0	0	1	1
0	1	0	1	1
1	0	0	1	1
1	1	0	0	1
0	0	1	1	1
0	1	1	1	1
1	0	1	1	1
1	1	1	0	0

Let’s now draw the basic gate for NAND (A, B).

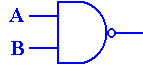
Now, examine the rearranged truth table.
When C = 0, the output is 1. This argues for the NAND of something and C.
When C = 1, the output is NAND(A, B). This may give us a lead on the circuit.

To force our thinking along the lines we have begun, I restate the NAND gate truth table,
using the variable C and another variable.

Y	C	Y·C	NAND
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

We see immediately that when C = 0, we have NAND(Y, C) = 1 independently of the value
of Y. Thus, the first criterion derived from the truth table will be satisfied automatically.

We see also that when C = 1, that NAND(Y, C) = NOT(Y). Our second criterion demands
that the output of the circuit be NAND(A, B) when C = 1. Thus we solve the equation

NOT(Y) = NAND(A, B)

The simple solution is Y = A·B, but this is not allowed, as we can use only NAND gates.
Thus we specify that Y = NOT (NAND(A, B) ). The last step to this puzzle is achieved
by noting that NAND(X, X) = NOT(X) for any input X. Now we have the circuit.

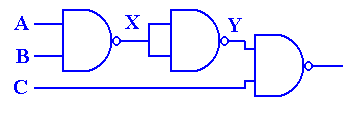
Here is another solution, discovered by one of the students.

Let X = NAND(A, B) = NOT(A·B) = (A·B)’.

Then Y = [(A·B)’·C] = (A·B)’’ + C’ = (A·B) + C’ = A·B + C’

The output is (Y·C)’ = [ (A·B + C’)·C]’ = [A·B·C + C’·C]’ = [A·B·C + 0]’ = [A·B·C]’

This is the NAND of the three inputs.

5. For this question, consider the Boolean variables X, Y, and Z with values
X = 1, Y = 0, and Z = 1. Evaluate the following Boolean expressions.

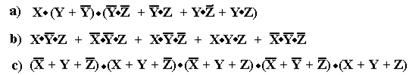
ANSWER: If X = 1, Y = 0, and Z = 1, then

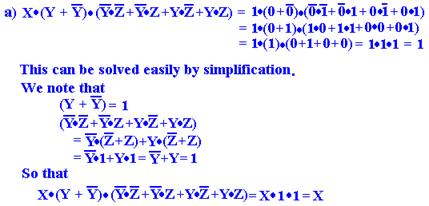
We solve the other two by noting that 1 + A = 1 for all A and 0·A = 0 for all A.
So that if X = 1, Y = 0, and Z = 1, we have the following.

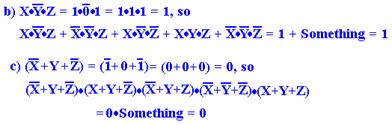
6 (10 points) Draw a circuit diagram to show how to implement
a) a three-input OR gate using only two-input OR gates.
b) a four-input OR gate using only three-input OR gates.

ANSWER: Here are a few answers. There are certainly more.

For F(X, Y, Z) = X + Y + Z, we have

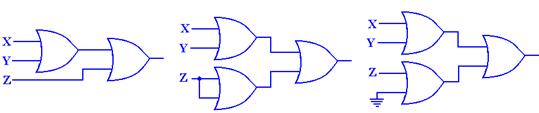
For F(W, X, Y, Z) = W + X + Y + Z, we have

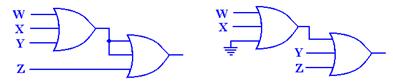
7 Represent the following function F(A, B, C) in the both canonical Sum of Products and
canonical Product of Sums form. Do not simplify this function.

A B C F

0 0 0 1

0 0 1 0

0 1 0 1

0 1 1 0

1 0 0 1

1 0 1 0

1 1 0 1

1 1 1 1

ANSWER: We begin by showing both the product and sum terms for each row. The rule
for transcribing a row into a canonical form depends on whether it is POS or SOP.
SOP Rule: Choose rows when F = 1
Variable is complemented if its row entry is 0, it is true otherwise
POS Rule: Choose rows when F = 0
Variable is complemented if its row entry is 1, it is true otherwise.

Applying the copy rules as stated above, we get the following results.

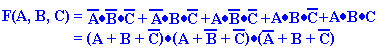
We might as well simplify the second form, just to show it can be done.

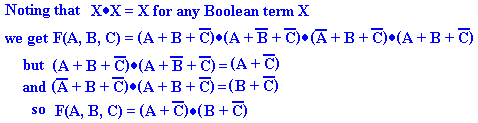
8 Draw a truth table for each of the following

a) Q = X·Y’ + X’·Z’ + X·Y·Z

Here is the truth table
X Y Z X’ Y’ Z’ X·Y’ X’·Z’ X·Y·Z Q
0 0 0 1 1 1 0 1 0 1
0 0 1 1 1 0 0 0 0 0
0 1 0 1 0 1 0 1 0 1
0 1 1 1 0 0 0 0 0 0
1 0 0 0 1 1 1 0 0 1
1 0 1 0 1 0 1 0 0 1
1 1 0 0 0 1 0 0 0 0
1 1 1 0 0 0 0 0 1 1

b) Q = (X’ + Y)·(X’ + Z’)·(X + Z)

Here is the truth table.
X Y Z X’ Z’ (X’ + Y) (X’ + Z’) (X + Z) Q
0 0 0 1 1 1 1 0 0
0 0 1 1 0 1 1 1 1
0 1 0 1 1 1 1 0 0
0 1 1 1 0 1 1 1 1
1 0 0 0 1 0 1 1 0
1 0 1 0 0 0 0 1 0
1 1 0 0 1 1 1 1 1
1 1 1 0 0 1 0 1 0

9 Describe the form for each of the following Boolean expressions.

a) F(X, Y, Z) = X·Y’ + Y·Z’ + Z’·Y’
b) F(A, B, C, D) = (A + B’ + C’)·(A’ + C’ + D)·(A’ + C’)
c) F(P, Q, R) = P·Q’ + Q·R’·(P + Q’) + (R’ + Q’)
d) F(A, B, C) = (A + B + C’)·(A’ + B’ + C’)·(A’ + B + C’)
e) F(A, B, C, D) = A·B·C’·D + A·B’·C’·D’ + A’·B’·C·D
f) F(A, B, C) = (A + B’ + C)·(A + B’)·(A + B + C’)

Solutions

a) F(X, Y, Z) = X·Y’ + Y·Z’ + Z’·Y’

This is a normal SOP expression. The last product term could easily be written as Y’·Z’
and normally would be so written; however, the order of literals is not important in
determining the form of an expression. The two terms Y’·Z’ and Y·Z’ both contain the
variables Y and Z, but the literals are different so we have no included terms.

Note that since Y’ + Y º 1, we can simplify this to F(X, Y, Z) = X·Y’ + (Y’ + Y)·Z’,
which becomes F(X, Y, Z) = X·Y’ + Z’.

b) F(A, B, C, D) = (A + B’ + C’)·(A’ + C’ + D)·(A’ + C’)

This is obviously a POS expression. It is also obvious that it is not a canonical form. The
first term by itself shows that the form is not canonical; it lacks a literal for the variable D.
We now note the second and third terms and see that the third term is included in the second
term, so the form is not normal. The answer is POS form, not a normal form.

As an exercise, we convert the expression (A + B’ + C)·(A’ + C’ + D)·(A’ + C’) into a
normal form. We use a form of the absorption theorem X·(X + Y) = X for any X and Y. We
see the truth of this theorem by considering two cases X = 0 and X = 1. For X = 0, the
identity becomes 0·(0 + Y) = 0 and for X = 1 it becomes 1·(1 + Y) = 1, both true. We now
consider the above with X = A’ + C’ and Y = D; thus (A’ + C’ + D)·(A’ + C’) = (A’ + C’)
and we obtain F(A, B, C, D) = (A + B’ + C)·(A’ + C’).

c) F(P, Q, R) = P·Q’ + Q·R’·(P + Q’) + (R’ + Q’)

This is not either a POS form or a SOP form, although many students wish to label it a SOP
form as it can be easily converted to SOP. Answer: Not in any normal form.

Again as an exercise, we convert the expression P·Q’ + Q·R’·(P + Q’) + (R’ + Q’) to a
normal form.

F(P, Q, R) = P·Q’ + Q·R’·(P + Q’) + (R’ + Q’)

= P·Q’ + P·Q·R’ + Q·Q’·R’ + R’ + Q’
= P·Q’ + P·Q·R’ + R’ + Q’ as Q·Q’·R’ = 0 for any value of Q
= P·Q’ + Q’ + P·Q·R’ + R’
= (P + 1)·Q’ + (P·Q + 1)·R’
= Q’ + R’ as 1 + X = 1 for any literal X.

Our simplification has dropped all but the last term in the original expression.

d) F(A, B, C) = (A + B + C’)·(A’ + B’ + C’)·(A’ + B + C’)

This is a canonical POS expression. We note that it can be simplified , noting that
(X + Y)·(X + Y’) = X for any X and Y (for Y = 0, the left hand side of the identity is
(X + 0)·(X + 1) = X; for Y = 1 it is (X + 1)·(X + 0) = X). To simplify, let X = A’ + C’ and
Y = B. So (A’ + B’ + C’)·(A’ + B + C’) = (A’ + C’) and F = (A + B + C’)·(A’ + C’).

e) F(A, B, C, D) = A·B·C’·D + A·B’·C’·D’ + A’·B’·C·D
This is a canonical SOP expression. Every term is a product term. The expression
is the logical OR of the terms, so we have a SOP expression. There are no included
terms – the first contains literal A, while the other two do not and the second contains
a C’ while the third does not. Thus the expression is a normal SOP. As each of the
three terms has a literal for each of the four variables, this is a canonical SOP.

f) F(A, B, C) = (A + B’ + C)·(A + B’)·(A + B + C’)
This is obviously some sort of POS expression. Each term is a sum term and the
expression is the logical OR of the terms. However, the second term (A + B’) is
contained in the first expression (A + B’ + C).
The expression is Product of Sums, but not normal.

We use the equality X·(X + Y) = X to simplify the expression. First we prove the
equality. For X = 0, we have
LHS = 0·(0 + Y) = 0·(Y) = 0
RHS = 0
For X = 1, we have
LHS = 1·(1 + Y) = 1·(1) = 1

RHS = 1

If we let X = (A + B’) and Y = C, we have an expression of the form
(X + Y)·X·(A + B + C’) = X·(A + B + C’) = (A + B’)·(A + B + C’).
This second expression is in Normal Product of Sums. The first term lacks a
literal for the variable C, so the expression is not in canonical form.

EXTRA QUESTION: What is the form of the expression F(P, Q, R) = Q’ + R’?
There are two answers – either Normal POS or Normal SOP.

It is clear that the expression is not canonical, as both terms lack a P. For an expression to
be canonical, each variable must appear in every term, in either the complemented or
non-complemented form.

SOP: Each of the two terms Q’ and R’ can be viewed as a product term. Admittedly, we
normally think of two or more literals (such as Q·R) when we say “product term”,
but a product term can have one literal. This is the logical OR of two product terms.

POS: Each of the two terms Q’ and R’ is a literal. The term (Q’ + R’) is a good sum term.
Here we have the product of one sum term, so POS.

As a follow-on, we note the forms of the expression F(Q, R) = Q’ + R’. The answer now is
either canonical POS or normal SOP, depending on how one wants to read it. As a canonical
POS, the expression has one sum term that contains a literal for each of Q and R. As a
normal SOP, we note that the first product term lacks a literal for R and the second product
term lacks a literal for Q, so the expression as an SOP is not canonical. However, it is the
sum of two product terms, with no inclusion.

10 Prove the following equality for Boolean variables X and Y by any valid means you
find convenient. Show all of your work.

A truth table provides the best proof. The functions and + X·Y match exactly.

X	Y	XÅY			X·Y	+ X·Y	Match?
0	0	0	1	1	0	1	Yes
0	1	1	0	0	0	0	Yes
1	0	1	0	0	0	0	Yes
1	1	0	1	0	1	1	Yes

11 Generate a truth-table for F(X, Y, Z) =

ANSWER: We first write this as to emphasize the blocks
that are negated. We then create the truth table.

X	Y	Z	Y·Z	X·Y·Z	X·(Y·Z)’	(X·Y·Z)’	F(X, Y, Z)
0	0	0	0	0	0	1	1
0	0	1	0	0	0	1	1
0	1	0	0	0	0	1	1
0	1	1	1	0	0	1	1
1	0	0	0	0	1	1	1
1	0	1	0	0	1	1	1
1	1	0	0	0	1	1	1
1	1	1	1	1	0	0	1

Notes: Generate the term in two parts. For X = 0, the term is 0.
For X = 1, the term is (Y·Z)’, the opposite of Y·Z.
Let A = X·Y·Z. This is of the form A + B + A’ = A + A’ + something = 1.

12 Produce a truth table for F(X, Y, Z) =

ANSWER: This is most easily cracked with algebra, noting that
we simply produce the truth table for (X + Y) · Z.

X	Y	Z	(X + Y)	(X + Y) · Z
0	0	0	0	0
0	0	1	0	0
0	1	0	1	0
0	1	1	1	1
1	0	0	1	0
1	0	1	1	1
1	1	0	1	0
1	1	1	1	1

13 Write the expression for the complement of F, if F =

ANSWER: First we solve a problem with the same form. If F(A, B, C) = A + B + C, then
what is the complement of F? We apply DeMorgan’s law twice to get the result.

Then

So

and

NOTES: Please remember that A + B · C + D is not the same as the expression
(A + B) · (C + D). By definition A + B · C + D = A + (B · C) + D.
One could also write (A + B) · (C + D) as (A + B)(C + D).

The next two problems refer to the following truth table.

X	Y	Z	F(X, Y, Z)
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

14 Represent the above truth table as a Boolean expression in SOP form.

ANSWER: One can write this expression as F(X, Y, Z) = S(0, 3, 6), as rows 0, 3, and 6
are the rows with F = 1. To write the SOP, we focus on these rows.
The term for row 0 is X’·Y’·Z’, as X = 0, Y = 0, and Z = 0 for the entry in that row.
The term for row 3 is X’·Y·Z, as X = 0, Y = 1, and Z = 1 for the entry in that row.
The term for row 6 is X·Y·Z’, as X = 1, Y = 1, and Z = 0 for the entry in that row.

The answer is F(X, Y, Z) = X’·Y’·Z’ + X’·Y·Z + X·Y·Z’.

15 Represent the above truth table as a Boolean expression in POS form.

ANSWER: One can also write the expression as F(X, Y, Z) = P(1, 2, 4, 5, 7), as rows
1, 2, 4, 5, and 7 are the rows with F = 0. To write the POS, we focus on these rows.
The term for row 1 is (X + Y + Z’) as X = 0, Y = 0, and Z = 1 for that row.
The term for row 2 is (X + Y’ + Z) as X = 0, Y = 1, and Z = 0 for that row.
The term for row 4 is (X’ + Y + Z) as X = 1, Y = 0, and Z = 0 for that row.
The term for row 5 is (X’ + Y + Z’) as X = 1, Y = 0, and Z = 1 for that row.
The term for row 7 is (X’ + Y’ + Z’) as X = 1, Y = 1, and Z = 1 for that row.

F(X, Y, Z) = (X + Y + Z’)·(X + Y’ + Z)·(X’ + Y + Z)·(X’ + Y + Z’)·(X’ + Y’ + Z’)

This function can obviously be simplified. I attempt a Q-M procedure.
Rows with one 1 0 0 1, 0 1 0, and 1 0 0
Rows with two 1’s 1 0 1
Rows with three 1’s 1 1 1

Combine 0 0 1 and 1 0 1 to get – 0 1. Combine 1 0 0 and 1 0 1 to get 1 0 –
Combine 1 0 1 and 1 1 1 to get 1 – 1
The terms are now – 0 1, 0 1 0, 1 0 –, and 1 – 1.
F(X, Y, Z) = (Y + Z’)·(X + Y’ + Z)·(X’ + Y)·(X’ + Z’)

16 This problem involves the circuit shown below.

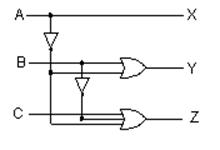
Give the Boolean expressions for X, Y, and Z as functions of the input variables A, B, and C.

ANSWER: This is a rather simple circuit, infelicitously drawn. What follows is a better
drawing that has been properly labeled to show the answers.

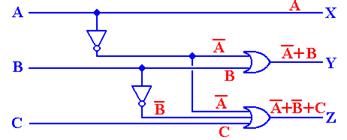
This circuit has several names, including a “multiple match resolver” and “priority arbitrator”
in that at most one of its outputs will be 0.

When A = 0 then X = 0, Y = 1, and Z = 1. (No dependence on B or C)

When A = 1 and B = 0 then X = 1, Y = 0, and Z = 1. (No dependence on C)

When A = 1, B = 1, and C = 0 then X = 1, Y = 1, and Z = 0.

When A = 1, B = 1, and C = 1 then X = 1, Y = 1, and Z = 1.

17 In the circuit for the above problem, what is the earliest time at which
all of the outputs (X, Y, Z) are valid if all of the inputs are set at T = 0.

ANSWER: X is valid immediately, but Y and Z are valid only at T ³ 2. T = 2.

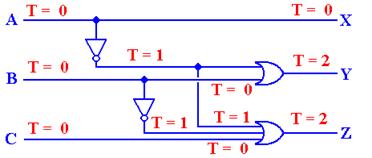
18 Draw a circuit diagram to show how to implement
a) a three-input AND gate using only two-input AND gates.
b) a four-input AND gate using only three-input AND gates.
c) a three-input AND gate using only one four-input AND gate.

COMMENT: This sort of thing happens often in a lab setting. You have a logical
design calling for 4–input gates, but the gates that you have in stock
are all 3–input. You must use at least two of what you have.

ANSWER:
a) Here are a few variants of this one.

b) Here are a few variants of this one.

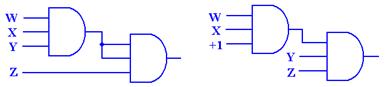
c) Here are two variants of this one.

19 This is an unusual problem that will require some thought.
There is nothing quite like it in the notes.

You are given two Boolean equations, using logical OR, logical AND, and logical NOT.
X + Y + Z = 1
· = 1
Solve these for the values of X, Y, and Z.

Answer: Consider the second equation first. Y’·Z’ = 1 if and only if Y’ = 1 and Z’ = 1.
This implies that Y = 0 and Z = 0.

The first equation X + Y + Z = 1 implies that one of the inputs to the logical OR
is 1. Since Y = 0 and Z = 0, we must have X = 1; X = 1, Y = 0, and Z = 0.

Here is another solution, based on a truth table. This is based on the observation that one
can solve sets of Boolean equations over N Boolean variables by trying all 2^N possible
combinations and seeing which ones work.

X	Y	Z	X+Y+Z	Y’	Z’	Y’·Z’	Match?
0	0	0	0	1	1	1	NO
0	0	1	1	1	0	0
0	1	0	1	0	1	0
0	1	1	1	0	0	0
1	0	0	1	1	1	1	YES
1	0	1	1	1	0	0
1	1	0	1	0	1	0
1	1	1	1	0	0	0

Only one row in the truth table has both X + Y + Z = 1 and Y’·Z’ = 1.

This row has X = 1, Y = 0, and Z = 0; it is the answer.

20. What does the following circuit do? Describe it using a truth table.

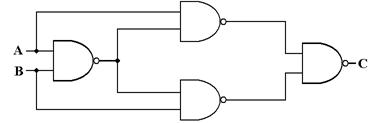
Remember that this circuit has four NAND gates, which are AND followed by a NOT.

Answer: We begin by labeling the diagram. In addition to C there are three outputs.

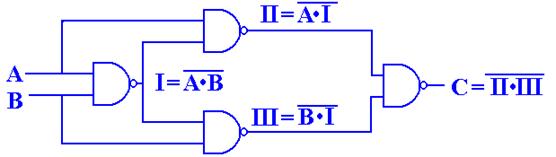
Now we place the truth table, with its necessary results.

A	B	I	II	III	C
0	0	1	1	1	0
0	1	1	1	0	1
1	0	1	0	1	1
1	1	0	1	1	0

This is C = A Å B, the exclusive OR.

COMMENT: The significance of this circuit is somewhat theoretical.

Remember the claim that one could use a NAND gate to make an AND, OR, or NOT gate.
Well, the NAND can also be used to make an XOR gate.

21 In the circuit below, what is the earliest time at which all of the outputs (X, Y, Z) are
valid if all of the inputs are set at T = 0.

ANSWER: X is valid immediately, but Y and Z are valid only at T ³ 2. T = 2.

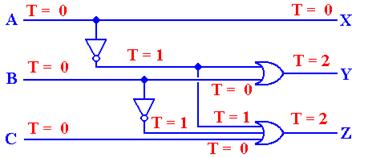
22 Using any proof method desired, prove that = X + Y for all X and Y.

ANSWER: This problem may be solved by a large number of ways. Here are a few,
beginning with the most obscure. The first answer uses a bit of simple algebra.

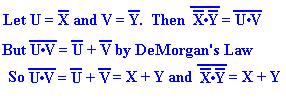
The second method is almost a duplicate of the first, but we state it anyway. Applying
DeMorgan’s law directly to the expression we get

Now we show a proof using the instructor’s famous “two-case” proof.
Let Y = 0. Then

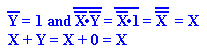
Let Y = 1, then

Since the left hand side is equal to the right hand side for both Y = 0 and Y = 1, we have
an equality.

We now present the more conventional truth-table proof.

X	Y					X+Y
0	0	1	1	1	0	0
0	1	1	0	0	1	1
1	0	0	1	0	1	1
1	1	0	0	0	1	1

The last two columns are equal for each of the four rows in the truth table, so the two
functions of two variables are equal.

23 Produce the truth-table for the Boolean function
G(A, B, C) = (A·B + C)·(A + B·C).

ANSWER: We first produce the truth table, and then offer a way to reflect on the answer.

A	B	C	A·B	B·C	A·B + C	A + B·C	G(A, B, C)
0	0	0	0	0	0	0	0
0	0	1	0	0	1	0	0
0	1	0	0	0	0	0	0
0	1	1	0	1	1	1	1
1	0	0	0	0	0	1	0
1	0	1	0	0	1	1	1
1	1	0	1	0	1	1	1
1	1	1	1	1	1	1	1

Another way to reflect on this truth table is to consider what happens based on A.

If A = 0, then G(A, B, C) = (A·B + C)·(A + B·C) = (0·B + C)·(0 + B·C)
= (0 + C)·(B·C) = B·C·C = B·C

If A = 1, then G(A, B, C) = (A·B + C)·(A + B·C) = (1·B + C)·(1 + B·C)
= (B + C)·1 = (B + C)

Just for fun, let’s simplify the above expression.
G(A, B, C) = (A·B + C)·(A + B·C) = (A·B + C)·A + (A·B + C)·B·C
= A·B·A + C·A + A·B·B·C + C·B·C
= A·B + C·A + A·B·C + B·C
= A·B + A·C + B·C + A·B·C
= A·B + A·C + B·C by the absorption theorem.

24 Produce the S-list and P-list representations of this function.

ANSWER:

The function has value 1 for rows 1, 2, 4, 5, and 7, so F(A, B, C) = S(3, 5, 6, 7)
The function has value 0 for rows 0, 3, and 6, so F(A, B, C) = P(0, 1, 2, 4).

25 Prove or disprove the following claim, by any convenient means.
Show all work necessary to support your argument.

Answer: The easiest way to disprove this claim is to use a truth table.

A	B	A Å B	(A Å B)’	A’	B’	A’ Å B’	Equal?
0	0	0	1	1	1	0	NO
0	1	1	0	1	0	1	NO
1	0	1	0	0	1	1	NO
1	1	0	1	0	0	0	NO

In fact, what we have proved is A’ Å B’ = A Å B.

26 Consider the exclusive OR expression, denoted by the symbol Å.
You are to examine the expression XÅYÅZ.

a) Prove that the expression XÅYÅZ makes sense, specifically you are asked
to prove that X Å [Y Å Z] = [XÅY]ÅZ for all X, Y, and Z.

b) Give the equivalent canonical SOP expression for this function.
This is most easily derived from the truth table.

ANSWER: a) We first give the complete proof, using a truth table.

X	Y	Z	X Å Y	Y Å Z	[X Å Y] Å Z	X Å [Y Å Z]
0	0	0	0	0	0	0
0	0	1	0	1	1	1
0	1	0	1	1	1	1
0	1	1	1	0	0	0
1	0	0	1	0	1	1
1	0	1	1	1	0	0
1	1	0	0	1	0	0
1	1	1	0	0	1	1

The simple form for the SOP is F(X, Y, Z) = å(1, 2, 4, 7).

Consider 0 0 1 0 1 0 1 0 0 1 1 1

X’Y’Z X’Y Z’ X Y’Z’ X Y Z

This cannot be simplified into an equivalent normal form.

I next give a few algebraic proofs, each of which depends on the identity

Here is a proof of that identity, using a truth table.

Y	Z	Y·Z	Y’·Z’	YÅZ	Y·Z + Y’·Z’	[YÅZ]’
0	0	0	1	0	1	1
0	1	0	0	1	0	0
1	0	0	0	1	0	0
1	1	1	0	0	1	1

We now offer a few algebraic proofs that X Å [Y Å Z] = [XÅY]ÅZ. We begin with
your instructor’s favorite method: the “two case” method.

If the equality holds both for X = 0 and X = 1, then the equality holds for all X, Y, and Z.

For X = 0, the first part is easily shown. For X = 1 it is a bit more tricky.
If X = 0, the left hand side is 0 Å [Y Å Z] = [Y Å Z].
If X = 0, the right hand side is [0ÅY]ÅZ = [Y Å Z].

If X = 1, the left hand side is 1 Å [Y Å Z], which becomes

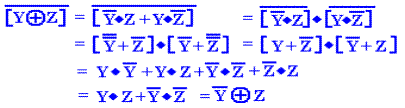
If X = 0, the right hand side is [1ÅY]ÅZ, which is immediately seen to be

Now, just to show I can do it, I shall give a complete algebraic proof.

We begin with the left hand side. By definition, we have

In the above work, I showed that

I can use this and the standard expansion of [Y Å Z] to get

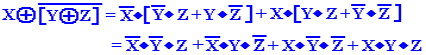
We now look at the right hand side of the equality and make use of previous results.

We can use the above reasoning to conclude immediately that

We complete the expansion to get the desired result.

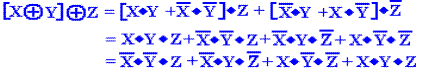
Did anyone notice that this is the sum function for a full adder?

PROBLEMS FOR SOLUTION

1. Using any proof method desired, prove that = X + Y for all X and Y.

2. Produce the truth-table for the Boolean function
G(A, B, C) = (A·B + C)·(A + B·C).

The next few problems are based on the following truth table.

A	B	C	F(A, B, C)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

3. Produce the S-list and P-list representations of this function.

4. Represent this function in both canonical SOP and canonical POS form.

5. Design a circuit using only AND, OR, and NOT gates to implement this function.

The next few problems are based on the function G(A, B, C) = P(2, 5).

6. Write the S-list representation of this function.

7. Represent this function in both canonical POS form and canonical SOP form.

8. Design a circuit using only AND, OR, and NOT gates to implement this function.

9. The notes show that the NAND gate is universal, in that one can use a NAND gate to
make an AND gate, OR gate, and NOT gate. Show how to use a NOR gate to make
an AND gate, OR gate, and NOT gate. Draw the circuit diagrams for these.

10. Use two 2-input OR gates to make a 3-input OR gate. Show the design.

11. Use a single 3-input OR gate to make a 2-input OR gate. Show the design.