The third list also displays logical adjacencies in its sequence: (X + Y) is logically adjacent to (X + Y’), which is logically adjacent to (X’ + Y’), which is logically adjacent to (X’ + Y). Using POS notation, we represent this list as 00, 01, 11, 10.
Consider the list of product terms when written in the more usual sequence
X’·Y’ X’·Y X·Y’ X·Y, or 00, 01, 10, 11 in the SOP notation.
In viewing this list, we see that the first term is logically adjacent to the second term, but that the second term is not logically adjacent to the third term: X’·Y and X·Y’ differ in two variables. This is seen also in viewing the numeric list 00, 01, 10, and 11. Note that each of the digits in 01 and 10 is different, so that 01 and 10 can’t represent logically adjacent terms.
Karnaugh Maps for 2, 3, and 4 variables
All books seem to define K-Maps for 2, 3, 4, 5, and 6 variables. It is this author’s opinion that K-Maps for 5 and 6 variables are a waste of time, so he will not discuss them. The reason for this opinion is that K-Maps are designed to be a simple tool for simplifying Boolean expressions; K-Maps with 5 or more variables are hopelessly complex.
This figure shows the basic K-Maps for 2, 3, and 4 variables. Note that there are two equivalent forms of the 3-variable K-Map; the student should pick one style and use it.

We now examine three equivalent forms of the K-Map of an unspecified function. We show these K-Maps only to comment on the form of K-Maps and not to discuss simplification.
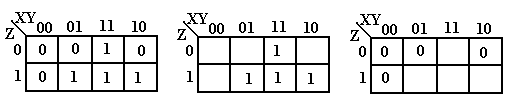
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
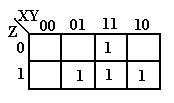
Each of these K-Maps represents the same function, shown at right in the truth-table form. One way to view a K-Map is as a truth-table with the main exception of the ordering 00, 01, 11, 10 seen on the top. For those interested, this ordering is called a Gray code.
The full K-Map is shown at left, with each square filled in either with a 0 or a 1. K-Maps are never written in this fashion – either one omits the 0’s or one omits the 1’s. The form omitting the 0’s is used when simplifying SOP expressions; to simplify POS one omits the 1’s.
One final note – K-Maps are used to simplify Boolean expressions written in canonical form.
K-Maps for Sum of Products (SOP)
Consider the Canonical SOP expression F(X,Y,Z) = X’·Y·Z + X·Y’·Z + X·Y·Z’ + X·Y·Z.
The first step in using K-Maps to simplify this expression is to use the SOP numbering to represent these as 0’s and 1’s. The negated variable is written as a 0, the plain as a 1. Thus, this function is represented as 011, 101, 110, and 111.
 Place
a 1 in each of the squares with the “coordinates” given in the list above. In the K-Map at left, the entry in the top
row corresponds to 110 and the entries in the bottom row correspond to 011,
111, and 101 respectively. Remember that
we do not write the 0’s when we are simplifying expressions in SOP form.
Place
a 1 in each of the squares with the “coordinates” given in the list above. In the K-Map at left, the entry in the top
row corresponds to 110 and the entries in the bottom row correspond to 011,
111, and 101 respectively. Remember that
we do not write the 0’s when we are simplifying expressions in SOP form.
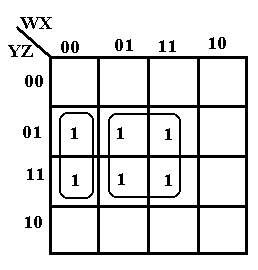
The next step is to notice the physical adjacencies. We group adjacent 1’s into “rectangular” groupings of 2, 4, or 8 boxes. Here there are no groupings of 4 boxes in the form or a rectangle, so we group by two’s. There are three such groupings, labeled A, B, and C.
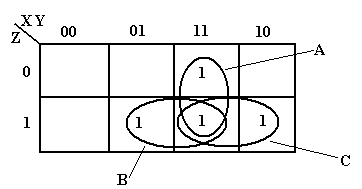 The
grouping labeled A represents the product term XY. The B group represents the product term YZ
and the C group represents the product term XZ.
Examine the B grouping: it has 011 and 111. In this we have Y and Z staying the same and
X having both values; thus the product term YZ.
This function is X·Y + X·Z + Y·Z.
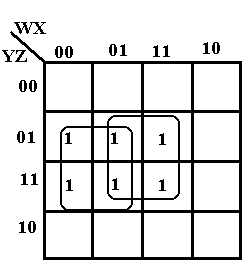
The
grouping labeled A represents the product term XY. The B group represents the product term YZ
and the C group represents the product term XZ.
Examine the B grouping: it has 011 and 111. In this we have Y and Z staying the same and
X having both values; thus the product term YZ.
This function is X·Y + X·Z + Y·Z.
The next example is to simplify F(A, B, C) = P(3, 5). We shall consider use of K-Maps to simplify POS expressions, but for now the solution is to convert the expression to the SOP form F(A, B, C) = S(0, 1, 2, 4, 6, 7). We could write each of the six product terms, but the easiest solution is to write the numbers as binary: 000, 001, 010, 100, 110, and 111.
 The
top row of the K-Map corresponds to the entries 000, 010, 100, and 110,
arranged in the order 000, 010, 110, and 100 to preserver logical
adjacency. The bottom row corresponds to
the entries 001 and 111. The top row
simplifies to C’. The first column
simplifies to A’B’ and the third column to AB.
Thus we have F(A, B, C) = A’·B’ + A·B + C’.
The
top row of the K-Map corresponds to the entries 000, 010, 100, and 110,
arranged in the order 000, 010, 110, and 100 to preserver logical
adjacency. The bottom row corresponds to
the entries 001 and 111. The top row
simplifies to C’. The first column
simplifies to A’B’ and the third column to AB.
Thus we have F(A, B, C) = A’·B’ + A·B + C’.
We next consider a somewhat offbeat example not in a canonical form.
F(W, X, Y, Z) = W’·X’·Y’·Z’ + W’·X’·Y’·Z + W·X’·Y’.
The trouble with K-Maps is that the technique is designed to be used only with expressions in canonical form. In order to use the K-Map method we need to convert the term W·X’·Y’ to its equivalent W·X’·Y’·Z’ + W·X’·Y’·Z, thus obtaining a four-term canonical SOP.
Before actually doing the K-Map, we first apply simple algebraic simplification to F.
F(W, X, Y, Z) = W’·X’·Y’·Z’ + W’·X’·Y’·Z + W·X’·Y’
= W’·X’·Y’·(Z’ + Z) + W·X’·Y’
= W’·X’·Y’ + W·X’·Y’
= (W’ + W)·X’·Y’ = X’·Y’
Now that we see where we need to go with the tool, we draw the four-variable K-Map.
F(W, X, Y, Z) = W’·X’·Y’·Z’ + W’·X’·Y’·Z + W·X’·Y’·Z’ + W·X’·Y’·Z. Using the SOP encoding method, these are terms 0000, 0001, 1000, and 1001. The K-Map is
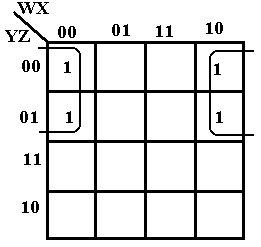
The first row in the K-Map represents the entries 0000 and 1000. The second row in the K-Map represents the entries 0001 and 1001. The trick here is to see that the last column is adjacent to the first column The four cells in the K-Map are thus adjacent and can be grouped into a square. We simplify by noting the values that are constant in the square: X = 0 and Y = 0. Thus, the expression simplifies to X’·Y’, as required.
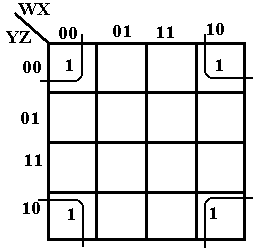
We close the discussion of SOP K-Maps with the example at
right, which shows that the four corners of the square are adjacent and can be
grouped into a 2 by 2 square. This K-Map
represents the terms 0000, 0010, 1000, 1010 or W’·X’·Y’·Z’ + W’·X’·Y·Z’ +
W·X’·Y’·Z’ +
W·X’·Y·Z’. The values in the square that are constant
are X = 0 and Z = 0, thus the expression simplifies to X’·Z’.
K-Maps for POS
K-Maps for Product of Sums simplification are constructed similarly to those for Sum of Products simplification, except that the POS copy rule must be enforced: 1 for a negated variable and 0 for a non-negated (plain) variable.
As our first example we consider F(A, B, C) = P(3, 5) = (A + B’ + C’)·(A’ + B + C’). Recall that the term (A + B’ + C’) corresponds to 011 and that (A’ + B + C’) to 101.
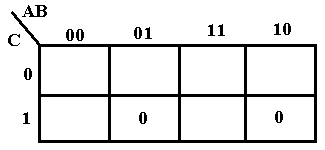
This is really somewhat of a trick question used only to illustrate placing of the terms for POS. Place a 0 at each location, rather than the 1 placed for SOP. Note that the two 0’s placed are not adjacent, so we cannot simplify the expression.
For the next example consider F2 = (A + B + C)·(A + B + C’)·(A + B’ + C)·(A’ + B + C). Using the POS copy rule, we translate this to 000, 001, 010, and 100.
Before we attempt to simplify F2, we note that it is a very good candidate for simplification. Compare the first term 000 to each of the following three terms. The term 000 differs from the term 001 in exactly one position. The same applies for comparison to the other two terms. Any two terms that differ in exactly one position can be combined in a simplification.
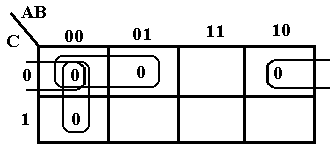 We
begin the K-Map for POS simplification by placing a 0 in each of the four positions
000, 001, 010, 100. Noting that 000 is
adjacent to 001, just below it, we combine to get 00– or
We
begin the K-Map for POS simplification by placing a 0 in each of the four positions
000, 001, 010, 100. Noting that 000 is
adjacent to 001, just below it, we combine to get 00– or
(A + B). The term 000 is adjacent to 010
to its right to get 0–0 or (A + C). The
term 000 is adjacent to 100 to its “left” to get –00 or (B + C). As a result, we get the simplified form. F2 =
(A + B)·(A
+ C)·(B
+ C)
Just for fun, we simplify this expression algebraically,
using the derived Boolean identity
X·X·X = X for any Boolean
expression X.
F2 = (A + B + C)·(A + B + C’)·(A + B’ + C)·(A’ + B + C)
= (A + B + C)·(A + B + C’)·(A + B + C)·(A + B’ + C)·(A + B + C)·(A’ + B + C)
= (A + B)·(A + C)·(B + C)
It is encouraging that we get the same answer.
We now consider simplification of a POS function specified by a truth table.
 A B
C F
A B
C F
0 0
0 1
0 0
1 1
0 1
0 0
0 1
1 1
1 0
0 1
1 0
1 1
1 1
0 0
1 1
1 1
We plot two 0’s for the POS representation of the function – one at 010 and one at 110. The two are combined to get –10, which translates to (B’ + C).
More Examples of K-Maps
The sample at left, based on an earlier design shows a particularly simple problem. We find that all the entries in the K-Map are covered with a single grouping, thus removing all three variables. Since the entire K-Map is covered, the simplification is F = 1.
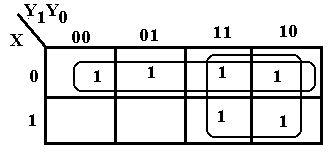 The
K-Map at right shows an example with overlap of two groupings of 1’s. All 1’s in the map must be covered and some
should be covered twice. The top row corresponds
to X’. We then form the 2-by-2 grouping
at the right to obtain the term Y1.
Thus F = X’ + Y1.
The
K-Map at right shows an example with overlap of two groupings of 1’s. All 1’s in the map must be covered and some
should be covered twice. The top row corresponds
to X’. We then form the 2-by-2 grouping
at the right to obtain the term Y1.
Thus F = X’ + Y1.
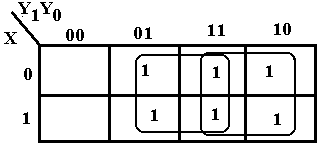 There
is another simplification that
There
is another simplification that
should be considered. This corresponds
to two 2-by-2 groupings. The 2-by-2
grouping at the right still corresponds to
Y1. The new 2-by-2 grouping in the
middle gives rise to Y0, so we get
another simplification F = Y0 + Y1.
Just One More K-Map: Overlapping Circles
We close the discussion of K-Maps with a technique that applies to both SOP and POS simplifications. We shall apply it to SOP simplification.
Consider the following K-Map.
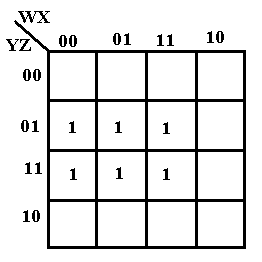
The six ones can be grouped in a number of ways. Consider the following.
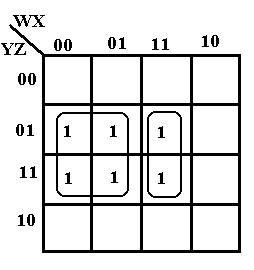
This grouping of four and two covers the six one’s in the K-Map.
The four ones in the square form the term W’·Z. The two ones in the rectangle form the term
W·X·Z.
The K-Map simplifies to W’·Z + W·X·Z.
 Another
way to consider the simplification of the K-Map is to group the rectangle and
the square as in the figure at right.
Another
way to consider the simplification of the K-Map is to group the rectangle and
the square as in the figure at right.
The rectangle corresponds to the term W’·X’·Z.
The square corresponds to the term X·Z.
This simplification yields W’·X’·Z + X·Z.
It is important to note that the groupings can overlap if this yields a simpler reduction.
 Here
we show two overlapping squares.
Here
we show two overlapping squares.
The square at left corresponds to the term W’·Z.
The square at right corresponds to the term X·Z.
This simplification yields W’·Z + X·Z, which is simpler than either of the other two forms validly produced by the K-Map method.
Try 1: W’·Z + W·X·Z
Try 2: W’·X’·Z + X·Z
Try 3: W’·Z + X·Z. This seems better.
Simplification with Don’t-Care Conditions
We now consider the use of K-Maps to simplify expressions that include the “d” or Don’t-Care condition often generated when considering digital designs using flip-flops. We give a number of examples related to our previous designs of sequential circuits.
|
|
X = 0 |
X = 1 |
|
Y1Y0 |
J1 |
J1 |
|
0 0 |
0 |
1 |
|
0 1 |
1 |
0 |
|
1 0 |
d |
d |
|
1 1 |
d |
d |
The general rule in considering a simplification with the Don’t-Care conditions is to count the number of 0’s and number of 1’s in the table and to use SOP simplification when the number of 1’s is greater and POS simplification when the number of 0’s is greater. Again we admit that most students prefer the SOP simplification. With a two-two split, we try SOP simplification.
|
Y1 |
Y0 |
X |
J1 |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
d |
|
0 |
1 |
1 |
d |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
d |
|
1 |
1 |
1 |
d |
First we should explain the above table in some detail. The first thing to say about it is that we shall see similar tables again when we study flip-flops. For the moment, we call it a “folded over” truth table, equivalent to the full truth table at right. The function to be represented is J1. Lines 0, 1, 4, and 5 of the truth table seem to be standard, but what of the other rows in which J1 has a value of “d”. This indicates that in these rows it is equally acceptable to have J1 = 0 or J1 = 1. We have four “Don’t-Cares” or “d” in this table; each can be a 0 or 1 independently of the others – in other words we are not setting the value of d as a variable.
Design with flip-flops is the subject of another course.
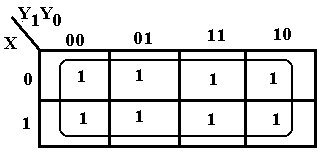
When attempting a K-Map for SOP simplification, we drop the
0’s and plot the 1’s and d’s.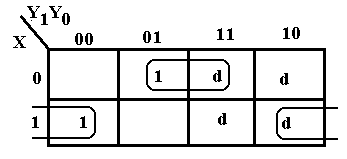 We then attempt to group the 1’s into 2-by-1,
2-by-2 groupings, etc. We use the d’s as
are convenient and have no requirement to cover any or all of them. Note that
We then attempt to group the 1’s into 2-by-1,
2-by-2 groupings, etc. We use the d’s as
are convenient and have no requirement to cover any or all of them. Note that
3-by-1 groupings are not valid and that the 2-by-2 grouping of d’s does not add
anything to the simplification, but only adds an extra useless term.
The terms in the top row, labeled 001 and 011 for X’Y1’Y0 and X’Y1Y0, simplify to 0–1 for X’Y0, and the terms in the bottom row, labeled 100 and 110 for XY1’Y0’ and XY1Y0’, simplify to 1–0 for XY0’, so the simplified expression is X’·Y0 + X·Y0’= XÅY0.
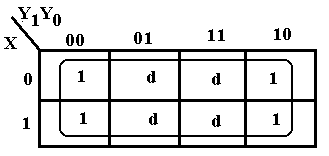
The sample at left, based on an earlier design shows a
particularly simple problem. We find
that using the d’s to combine with the 1’s to produce a
4-by-2 grouping of 1’s. Since the entire
K-Map is covered, the simplification is F = 1.
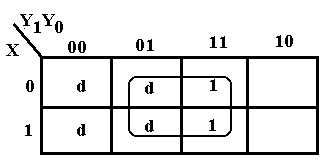
 The
K-Map at right corresponds to an input table with one 0 and three 1’s. This immediately suggests a SOP approach to
the K-Map; we plot the 1’s and d’s and drop the 0. The top row corresponds to X’. We then form the
The
K-Map at right corresponds to an input table with one 0 and three 1’s. This immediately suggests a SOP approach to
the K-Map; we plot the 1’s and d’s and drop the 0. The top row corresponds to X’. We then form the
2-by-2 grouping at the right to obtain the term Y1. Thus F = X’ + Y1.
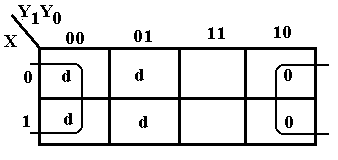
 There
is another simplification that
There
is another simplification that
should be considered. This corresponds
to two 2-by-2 groupings. The 2-by-2
grouping at the right still corresponds to
Y1. The new 2-by-2 grouping in the
middle gives rise to Y0, so we get
another simplification F = Y0 + Y1.
|
|
X = 0 |
X = 1 |
|
Y1Y0 |
K0 |
K0 |
|
0 0 |
d |
d |
|
0 1 |
d |
d |
|
1 0 |
0 |
0 |
|
1 1 |
1 |
1 |
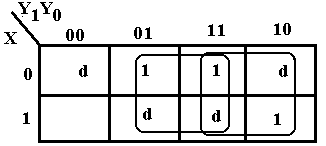
As a final example, we consider the input table, which contains two 0’s and two 1’s. According to the theory, this could be simplified equally well either as a SOP or POS expression. To gain confidence, we do both simplifications, with the SOP first.
Considered as a SOP problem, we plot the 1’s and d’s, then form the largest possible group that covers all of the 1’s. Note that 3-by-2 is not a valid grouping, so we go with the 2-by-2 grouping. The square corresponds to Y0. The top row simplifies to 0–1 and the bottom to 1–1, thus we have – – 1 or Y0.
The POS simplification is shown at left. The top row simplifies to 0–0 and the bottom row simplifies to 1–0 so the K-Map simplifies to – – 0. Using the POS copy rule, this translates to Y0, as before. It’s a good thing that the two methods agree.
A Diversion: Application of Simplification Techniques to
Programming
This next section attempts to apply some of the Boolean simplification techniques to issues sometimes seen in software development, especially C++ programming.
Consider the Boolean expressions in C++ that relate to equality. For variable x, we can have expressions such as (x == 0), (x != 0), and !(x == 0). The last two are logically identical, and all are distinct from the assignment statement (x = 0), which evaluates to False.
In our diversion, we consider three variables: x, y, and z. The only assumption made here is that each of the three is of a type that can validly be compared to 0; assuming that all are integer variables is one valid way to read these examples. Each of the expressions (x == 0), (y == 0), and (z == 0) evaluates to either T (True) or F (False).
Consider a function that is to be called conditionally based on the values of three variables:
x, y, and z. We write the Boolean expression as follows
if ( ( (x != 0) &&
(y != 0) && (z != 0) )
|| ( (x != 0) &&
(y != 0) && (z == 0) )
|| ( (x != 0) &&
(y == 0) && (z == 0) )
|| ( (x == 0) &&
(y != 0) && (z != 0) )
|| ( (x == 0) &&
(y != 0) && (z == 0) )
|| ( (x == 0) &&
(y == 0) && (z == 0) ) ) y = fzero( )
We can apply the truth-table approach to analysis of the conditions under which the function fzero is invoked. The following table illustrates when the function is to be called.
|
(x == 0) |
(y == 0) |
(z == 0) |
Call fzero |
|
F |
F |
F |
Yes |
|
F |
F |
T |
Yes |
|
F |
T |
F |
No |
|
F |
T |
T |
Yes |
|
T |
F |
F |
Yes |
|
T |
F |
T |
Yes |
|
T |
T |
F |
No |
|
T |
T |
T |
Yes |
If this looks a bit like a truth table, it is because it is equivalent to a truth table and can be converted to one. Consider the following definitions of Boolean variables A, B, and C.
A = (x == 0)
B = (y == 0)
C = (z == 0)
Consider the expression A = (x == 0) in the C++ programming language. It may seem a bit strange, but is perfectly legitimate. The expression (x == 0) is a Boolean expression – it evaluates to True or False. The variable A is a Boolean variable, it also takes on one of the Boolean values. In order to translate the table above into a truth table that we recognize, we replace the expressions (x == 0), (y == 0), and (z == 0) by their equivalents – the Boolean variables A, B, and C. We are beginning to construct a Truth Table.
In order to apply the truth table approach to this problem,
we must define a Boolean function. For
our purpose, we define F(A, B, C) as follows
F(A, B, C) = 1 if
fzero is called
= 0 if fzero is not
called
Returning to our convention of 0 for False and 1 for True, we have the truth table.
|
A |
B |
C |
F(A, B, C) |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
This is a truth table that we have considered and simplified in an earlier section of the work. Using terminology we have already discussed, we see that this function F(A, B, C) can be expressed as either a SOP with six product terms or a POS with two sum terms. Reading this as a POS, we get
![]() , which simplifies to
, which simplifies to ![]() .
.
We now convert back to the original notation. Recalling that
B = (y == 0) and C = (z == 0), we note that B’ = (y != 0) and the condition for
calling the function fzero becomes ( (y != 0) || (z
== 0) ). So the equivalent (and much
simpler) expression is
if ( (y !=
0) || (z == 0) ) y = fzero( )
Consider now the Boolean expression ( (x == 0) || ( (x != 0) && (y == 0) ) ). In an attempt to simplify this expression we define two Boolean variables
A = (x == 0)
B = (y == 0)
Recall that (x != 0) = !(x == 0) = ![]() . In our
terminology, the expression is
. In our
terminology, the expression is
F(A, B) = ![]()
There are a number of ways to simplify this expression. The first, and least obvious, is to invoke the theorem of absorption, which states that the formula equals A + B.
To illustrate other options, we expand the above to canonical SOP and then examine it by means of both a truth table and a K-map. To expand the expression into canonical SOP, we need to have the first term contain a literal for the variable B.
![]()
The truth table for this expression is
|
A |
B |
F(A, B) |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
Representing this as a POS formula, we immediately get F(A, B) = (A + B), which translates to the C++ expression ( (x == 0) || (y == 0) ).
As a final example, consider the following Boolean expression in C++
( (x == 0) || (y == 0) || (z == 0) ) && ( (x == 0) || (y == 0) || (z !=0)) &&
( (x == 0) || (y != 0) || (z == 0) ) && ( ( x != 0) || (y == 0) || (z == 0) )
Define A = (x == 0)
B = (y == 0)
C = (z == 0)
With these definitions our expression becomes
![]()
This is known to simplify to
F(A, B, C) = (A + B)·(A + C)·(B + C)
So our Boolean expression in C++ simplifies to
( (x == 0) || (y == 0) ) && ( (x == 0) || (z == 0) ) && (y == 0) || (z == 0) )
Inspection of the above shows that we want at least two of (x
== 0), (y == 0), and (z == 0) to be true.
Compare this with the original derivation of the function
F(A, B, C) = (A + B)·(A +
C)·(B
+ C)
used for the carry-out of a Full-Adder, which is 1 if two or three of the inputs are 1.