The MAR is a 26–bit register that contains the address into physical memory. This figure shows the mapping of 20-bit program addresses into 26–bit real addresses, using the six page number bits found in the PSR. Bus B3 supplies the 20 low–order address bits to the MAR, these being copied from the 20 low–order bits of the IR (Instruction Register).

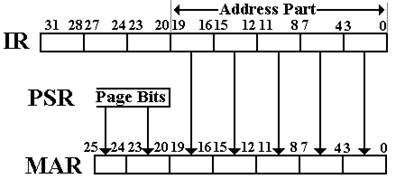
Figure: Conversion of Program Addresses

From the viewpoint of the program, all address registers are 20–bit registers. This includes the Program Counter (PC) and the Stack Pointer (SP). All address calculations, including indexed and indirect addressing are done modulo 2²⁰ and yield an unsigned 20–bit binary number that is passed to the 20 low–order bits of the MAR. This odd arrangement does serve to force separation of process address spaces; no process can access the memory allocated to another. This is a convenient security feature, although it is a bit rigid.

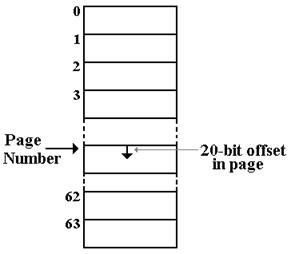
Figure: Program Addressing with the Page Structure

To summarize the situation, each program issues 20–bit addresses (representable as 5 hex digits) that are offsets into a memory page of size 2²⁰ (1,048,576) 32–bit words. This is converted to a 26–bit address sent to the MAR for actual memory access. For example, if the page number is 23 (hex 0x17) and the 20–bit address is 0x54321, the 26–bit address is 0x1754321. As this is a 26–bit address, the high–order hexadecimal digit is less than 4, so that the address can be considered as 28–bits with the first two bits forced to 00.

Specifications for the Boz–7

Further specifications of the computer, called the Boz–7, are as follows.

1) It is a stored program computer; i.e., the computer memory is used to store
both data and the machine language instructions of the program under execution.

2) It is a Load/Store machine; only register loads and stores access memory.

      3)   The Boz–7 is a 32–bit machine. The basic unit of data is a 32–bit word. This
            is in contrast to machines, such as the Pentium class, in which the basic data
            unit is the byte (8 bits) although the basic integer size is usually 32 bits.

      4)   This is a two’s-complement machine. Negative numbers are stored in the
            two’s-complement form, so the arithmetic is said to be two’s-complement. The
            range for integer values in from – 2,147,483,648 to 2,147,483,647 inclusive.

5) Real number arithmetic is not supported. We may envision the computer as
a typical RISC, with an attached floating point unit that we will not design.

6) The CPU uses a 26–bit Memory Address Register (MAR) to address memory.

7) The memory uses a 32–bit Memory Buffer Register (MBR) to transfer data to and
from the Central Processing Unit.

8) The CPU uses a 16–bit I/O Address Register (IOA) to address I/O registers.

9) The CPU uses a 32–bit I/O Data Register (IOD) to put and get I/O data.

      10) The Boz–7 uses 20-bit addressing and the entire address space is occupied. The
            memory is 32–bit word-addressable, for a total of 2²⁰ (1 048 576) words. It is not
            byte-addressable. One advantage of this addressing scheme is that we may ignore
            the byte ordering problem known as Big Endian – Little Endian.

11) The Boz–7 has a 5–bit op-code, allowing for a maximum of 2⁵ = 32 different
instructions. By design, not all op-codes have been assigned.

12) The Boz–7 uses isolated I/O with the dedicated instructions GET and PUT.

      13) The Boz–7 has four addressing modes: direct, indirect, indexed, and
            indexed-indirect. In addition, two instructions allow immediate addressing.
            Indexed-indirect addressing is implemented as pre-indexed indirect. This decision
            allows implementation of register indirect addressing, a fifth address mode.

      14) The Boz–7 has eight general purpose registers, denoted %R0 through %R7
             Each of these registers is a 32–bit register, able to hold a complete memory word.
                   %R0 is identically 0. It is not used to store any number but the constant 0.
                   %R1 through %R7 is read/write registers, used to store results of computation.

Each of the eight registers can be used as an index register or as the source operand for an instruction. Only registers %R1 – %R7 can be changed by arithmetic or register load operations. Attempts to change %R0 are undertaken for side effects only.

NOTE: The reason for selection of eight registers and not more is that the 3–bit register select field fit neatly into the preferred instruction format, while a 4–bit field did not.

Program Status Register (PSR)

Here is the structure of the 32–bit processor status register (PSR), also called the program status register. Note that not all bits are assigned.

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16
Not presently assigned.										6–bit Page Number

15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
Security Flags						V	C	Z	N	R = 00		I	CPU Priority

Bits 2 – 0 of the PSR specify a three-bit unsigned integer corresponding to the CPU priority. This unsigned integer corresponds to a CPU priority in the range 0 to 7 inclusive.

I/O device priority is one of 4, 5, 6, or 7. Levels 1, 2, and 3 are used for software interrupts, which are the preferred mechanism by which a user program will invoke services of the operating system. User programs almost always execute at priority 0.

Bit 3 is the interrupt bit, used to allow or disallow the raising of interrupts by input/output devices. If this bit is zero, then interrupts are blocked. Such a setting may be required by the operating system in the initial processing of an interrupt to block other interrupts.

Bits 5 – 4 of the PSR are reserved, with each bit hardwired to logic 0 in the current design. It is common practice for computer designs to have reserved bits, as opposed to bits that are just not used. In this design, reserving the bits allows for more priority levels in the future.

Bits 9 – 6 of the PSR reflect the effect of the last arithmetic operation.
            C         Carry bit                      the last operation generated a carry out.
                                                            Not a problem; useful for multi-precision arithmetic.
            N         Negative bit                the result of the last operation was negative.
            Z          Zero bit                       the result of the last operation was zero.
            V         Overflow Bit               the last operation caused a numeric overflow.

Question:        How to set the N, Z, and C bits based on the last ALU operation.
Answer:          The control unit will do this as a part of executing the arithmetic.
                        These bits cannot be set by loading the PSR.

Bits 15 – 10 of the PSR are used as security flags, allowing the operating system to assign privileges to other programs. Specific privileges might include: access to I/O devices, memory management and process scheduling, and access to all files in the file system.

The current design is more of a reaction to the UNIX user/super–user model in which a program has either no privileges or has every privilege. At present, we shall not be more specific on assignment of these bits to privilege levels. When the operating system runs in the UNIX “super–user” mode, it has privilege 63₁₀ = 111111₂.

Bits 21 – 16 of the PSR determine which of the 64 memory pages is allocated to the process. The memory is divided into pages of 2²⁰ words and the program can use only one of them.

Bits 31 – 22 of the PSR are presently not assigned any function and may serve any number of uses in the future. Because they are not reserved, system software may use them.

General comments on 32–bit words

We shall use eight hexadecimal digits to represent the 32–bit binary values stored in the
Boz–7 memory words. This notation is used for character data, integer data, and instructions. We use bit numbering in which bit 31 is on the left and bit 0 is on the right, so that the bits as read from left to right are from the most significant to least significant.

Character Data Format

The Boz–7 will be viewed as storing character data in the 8–bit ASCII format or 16–bit UNICODE (if we are to be more modern). Standard 8–bit ASCII data would be stored four characters to the memory word and manipulated four characters at a time. Characters would be numbered in the word according to the following convention.

Bits	31 to 24	23 to 16	15 to 8	7 to 0
Character	3	2	1	0

This course will focus on integer data. It is not that character data are unimportant, it is just that we need simple examples so that we can focus on the hardware and not on the data.

Integer Data Format

The Boz–7 stores signed integers as 32–bit two’s-complement numbers. The range of integers that can be stored and processed directly by the CPU is – 2,147,483,648 ( – 2³¹ ) to 2,147, 483, 647 ( 2³¹ – 1), inclusive. Other precision arithmetic ( 8–bit, 16–bit, and 64–bit) are not supported by this design, though they would be useful in a real computer.

Real Number Format

The Boz–7 is not designed to process real numbers, also called floating point numbers. If it did, it would use IEEE–754 single-precision format and use an attached coprocessor to do the calculations. In this regard, it would be typical of RISC–type processors in allocating floating point execution to an attached processor. We shall ignore floating-point numbers.

The Assembly Language of the Boz–7

The assembly language of a computer represents the lowest level instructions that the computer can execute directly. Some of us have to program computers in assembly language and most of us (thankfully) do not have that task. The main issue in favoring a higher level language over assembly language is programmer productivity. If a programmer can write only so many lines of code per day (there are good measures of this), then it is better that he or she write lines of code that translate into many assembly language instructions that if each line of code translates only into one such instruction.

In computer architecture, we view assembly language statements as the “functional specifications” of the computer, in that each such statement indicates a specific action that the computer must complete. The assembly language of this computer has been designed to present a typical collection of functions typically found on a modern machine. Once we have stated what the computer must do, we design the computer to do exactly that.

The instructions in the assembly language of the Boz–7 are listed below, in numeric order of the op-codes. Note that not all 32 op–codes are used in this version of the design. The reader will note an unexplained gap in the operation code sequence. This gaps will facilitate the design of the CPU control unit by considerably simplifying its circuitry.

Op-Code	Mnemonic	Description
00000	HLT	Halt the Computer
00001	LDI	Load Register from Immediate Operand
00010	ANDI	Logical AND Register with Immediate Operand
00011	ADDI	Add Signed Immediate Operand to Register
00100	NOP	Not Yet Defined – At Present it is does nothing
00101	NOP	Not Yet Defined – At Present it is does nothing
00110	NOP	Not Yet Defined – At Present it is does nothing
00111	NOP	Not Yet Defined – At Present it is does nothing
01000	GET	Input to Register
01001	PUT	Output from Register
01010	RET	Return from Subroutine
01011	RTI	Return from Interrupt (Not Implemented)
01100	LDR	Load Register from Memory
01101	STR	Store Register into Memory
01110	JSR	Subroutine Call
01111	BR	Branch on Condition Code to Address
10000	LLS	Logical Left Shift
10001	LCS	Circular Left Shift
10010	RLS	Logical Right Shift
10011	RAS	Arithmetic Right Shift
10100	NOT	Logical NOT (One’s Complement)
10101	ADD	Addition
10110	SUB	Subtraction
10111	AND	Logical AND
11000	OR	Logical OR
11001	XOR	Logical Exclusive OR

Privileged Instructions
In a multi–user computer, some instructions must be reserved for use by the Operating System and its system programs. These include access to I/O devices (our instructions are GET and PUT) to preclude the simultaneous use of such devices by more than one process. Other privileged instructions would be those to manipulate the Program Status Register and directly access the Stack Pointer. The stack pointer is changed by both PUSH and POP instructions, which are not privileged; but it required O/S privilege to initialize its value.

A modern assembler would convert a number of instructions to operating system calls, often called “traps”, “software traps”, or “software interrupts”. These include:
            HLT    translated into a return to the Operating System (which terminates the
                        process, reallocates memory, and starts another process),
            GET    translated into a call to an Operating System routine to get input, and
            PUT     translated into a call to an Operating System routine to output data.

Addressing Modes

The Boz–7 computer may be said to support five addressing modes: immediate addressing and four true addressing modes, which are direct, indirect, indexed, and indexed-indirect. As this is a Load/Store machine, these modes are limited to certain instructions, specifically the following four instructions that will be used to illustrate the addressing modes

LDI Load Register Immediate
ADDI Add Register Immediate

LDR Load Register from Memory
STR Store Register to Memory

Of these instructions, only the first two can use immediate addressing. Only the second two instructions can use the other four addressing modes to address memory. As an aside, we shall see that the I/O instructions (discussed below) can be considered to use direct addressing in that the argument specifies the address of the I/O register. However, we note that these instructions do not address memory and so give them minimal coverage here.

One of the main differences between a RISC device, such as our computer, and a CISC device such as the VAX–11/780 (now obsolete) is that the latter can issue arithmetic commands that involve the memory directly; such as ADD X, Y to add directly the contents of the two memory locations and place the result into one of them. In our computer, only a general–purpose register can be the target of an ADD instruction, and the operands must be either both registers or one register and an immediate operand. This is the major design constraint of a load/store architecture. It has been discovered that the increase in CPU performance more than pays for the inconvenience of this design constraint.

To differentiate the immediate address mode from other address modes, let’s consider a simple instruction set with two modes of addressing (direct and immediate) and a single accumulator, which is loaded by the instruction called LOAD. What does the instruction LOAD 100 do? In immediate mode, the register is loaded with the value 100. Thus we see that the immediate mode should not be called an address mode, as no memory address is used; the argument is coded immediately in the instruction. In direct mode, the register is loaded with the value of the memory word at address 100.

Immediate Addressing

Most computer architectures call for immediate instructions to have the argument encoded directly within the 32–bit machine word representing the instruction. In these designs, immediate instructions do not reference computer memory to access arguments and thus differ from other addressing modes in which the machine instruction encodes an address for an argument in main memory. One notable difference is found in the ISA (Instruction Set Architecture) for the IBM mainframe series (S/360, S.370, z/9, z/10, etc.) in which an immediate instruction has two operands, one of which is a memory reference and one of which is encoded within the instruction. We shall not use that type of instruction here.

In the Boz–7, the lower order 20 bits of the machine instruction (bits IR₁₉ – IR₀) are used by many instructions to store either the argument (immediate addressing) or an address used to locate the argument in memory (other addressing modes).

I/O Device Register Addressing

The two I/O instructions, GET and PUT, reference I/O devices by a 16–bit address on the I/O bus, which is separate from the memory bus. The MAR is not involved in this addressing, as it uses a register named IOA that accesses the I/O device registers. As indicated above, this type of addressing can be viewed as direct addressing, except that the term is reserved for discussions of memory addressing. The use of device registers to access I/O devices is explained in the chapter on Input/Output.

Memory Addressing

It should be understood that only four instructions actually compute memory addresses. These four instructions can use any of the available addressing modes.
LDR and STR the address of the argument.
BR and JSR the address of the jump target.

The Boz–7 computer may be said to support five addressing modes, which are direct, indirect, register-indirect, indexed, and indexed–indirect. These addressing modes are built around two primitive operations.

Indirection: This is similar to the use of pointers in some modern languages.
Indexing: This is similar to the use of indices in accessing arrays.

We note that there are two possible varieties of indexed–indirect addressing, depending on whether the indexing is done first or the indirection is done first. Generally speaking, we may view these two in terms for describing higher–level languages as follows.
Pre–indexed indirect an array of pointers.
Post–indexed indirect a pointer to an array.

Many computers will support both modes, but the Boz–7 computer supports only
pre-indexed indirect. This is due to the design requirement that the CPU be simple.

The four true addressing modes are constructed from these two primitives, according to the following table.

	Indexing Not Used	Indexing Used
Indirection Not Used	Direct Addressing	Indexed Addressing
Indirection Used	Indirect Addressing	Indexed-Indirect Addressing

All address calculations are performed modulo 2²⁰ (modulo 1048576), so that no addresses outside the permissible range of memory addresses are generated. All addresses are interpreted as unsigned 20–bit integers.

When bits 19 through 0 of the IR form an immediate address, they are interpreted as an
20–bit integer; either unsigned (for the ANDI) or two’s–complement for the LDI and ADDI. Specifically the ranges are:
            ANDI              0 to 2²⁰ – 1, representable as five hexadecimal digits, but best
                                    viewed as a collection of twenty Boolean bits with no numeric value.
            LDI, ADDI     – 2¹⁹ to 2¹⁹ – 1, or – 524, 288 to 524, 287.

Effective Address

Each of the four true addressing modes references a word in memory. We say that each of these modes gives rise to an effective address, that is the address of the operand being indicated by the specified mode. We use the following memory lay-out as an aid in our discussion of the addressing modes and the corresponding effective addresses. For each of the examples, we consider the LDR instruction that loads the accumulator from the location indicated by the effective address.

In what is below, we let the symbol Z stand for 0x0A, or 10 in decimal. We assume that memory in the vicinity of this address is laid out in the following map, and that the contents of register 3 are 7; denoted by (%R3) == 7.

Address	5	6	7	8	9	A	B	C	D	E	F	10	11
Contents	11	32	2C	1E	56	5	7A	10	3	F	E	D	8

Figure: Sample Address Map (All values are hexadecimal)

In immediate addressing, there is no access to memory and no effective address. The effect of the instruction LDI %R1, Z is the same as LDI %R1, 10; register %R1 gets the value 10.

We use the idea of an effective address as a part of determining the effect of the instruction. For register load instructions, the effect of the instruction is that the register has a given value stored into it. For the true addressing modes, this value depends on the effective address. If we use the term “EA” to represent effective address, what happens in the four true addressing modes is that the target register gets the contents of Memory[EA].

LDR: Register ¬ M[EA]

A word of caution is now in order. We shall discuss assembly language statements such as LDR %R1, Z, in which Z is considered as an address. This is in contrast to high-level language statements such as X = Z, in which Z is the value stored at some address. For a high-level language, the compiler associates a memory location with each variable, so that the variable Z is associated with an address, z, and we retrieve Memory[z].

Direct Addressing

LDR %R1, Z

Recall that Z is an address, not the value stored at that address.

For direct addressing the effective address is EA = Z

The effect is %R1 ¬ M[ Z ]

Here %R1 gets M[0x0A] = 5, after the register load %R1 == 5.

Indirect Addressing

LDR %R1, * Z

The effective address is EA = M[Z] = M[0x0A] = 5

The effect is %R1 ¬ M[ M[Z] ] = M[ M0x0A] ] = M[5] = 11

Here %R1 gets M[5], after the register load %R1 == 11

Indexed Addressing

LDR %R1, Z, 3

The effective address is EA = Z + (%R3) = A + 7 = 11

The effect is %R1 ¬ M[ Z + (%R3)] = M[0xA + 7] = M[0x11] = 8

Here %R1 gets M[0x11]; after the register load %R1 == 8

Register-Indirect Addressing

LDR %R1, *(3)

This occurs when the address Z = 0. In this case the register holds the effective address.

The effective address is EA = (%R3) = 7.
The effect is %R1 ¬ M[ (%R3) ] = M [7] = 2C.

Here %R1 gets M[0x11]; after the register load %R1 == 2C

Indexed-Indirect Addressing

LDR %R1, * Z, 3

There are two types of indexed-indirect addressing, depending on the order of operations.

In preindexed-indirect addressing, the indexing is done first, then the indirection.
In postindexed-indirect addressing, the indirection is done first, then the indexing.

Preindexed-Indirect

The effective address is EA = M[Z + (%R3)] = M[0x0A + 0x07] = M[0x11] = 8

The effect is %R1 ¬ M[ M[ Z + (%R3)]] = M[0x08] = 0x1E.

Think of this as an array of pointers. The address Z + (%R3) refers to an array entry that is used as a pointer to the addressed entry.

Postindexed-Indirect

The effective address is EA = M[Z] + (%R3) = M[0x0A] + 7 = 11 = 5 + 7 = C

The effect is %R1 ¬ M[ M[ Z] + (%R3)] = M[0x0C] = 10.

Think of this as a pointer to an array. The address Z holds a pointer to an array at address M[Z]. This array is indexed by %R3.

It is important for the student to understand the difference between the two varieties of indexed-indirect addressing. Many computers will implement both types of addressing, but the Boz–7 implements only one, in order to simplify the design.

The Boz–7 design implements more addressing modes than a typical RISC design. This is due to its use as a teaching tool and the need to discuss these addressing modes.

Syntax of the Assembly Language

We now characterize the syntax of each type of assembly language statement as used in the Boz–7 computer. One reason to do this is to keep the instructor from getting confused.

Immediate Operations

The syntax of the immediate operations is quite simple.

Syntax Example

      LDI %Rn, value           LDI %R3, 100
      ANDI %Rn, value        ANDI %R5, 0xFFA08   -- Bit masking is easier in hexadecimal.
      ADDI %Rn, value        ADDI %R5, 200
      NOP                             NOP                                -- Not much to say on this one.

It is expected that the following operations will be common enough to warrant syntactic sugar in the assembly language.

            LDI %Rn,    0             Clear the register
            ADI %Rn,    1             Increment the register
            ADI %Rn, – 1             Decrement the register

Input / Output Operations
Syntax Example

      GET %Rn, I/O_Register   GET %R2, XX           Load the general-purpose register from
                                                                                    the I/O device register.
      PUT %Rn, I/O_Register   PUT %R0, YY            Store the contents of register into the
                                                                                    I/O device register.

Load/Store Operations

The syntax of these is fairly simple. For direct addressing we have the following.

            Syntax                                     Example
            LDR %Rn, address                 LDR %R3, X              Loads %R3 from address X
            STR %Rn, address                  STR %R0, Z               Loads %R0 into address Z
                                                                                                This clears address Z.

Other variants of the syntax are illustrated in the discussion on addressing modes.

Branch

The syntax of this instruction, and its variants, is quite simple.

Syntax Example

BR address BRU W Note that this can use all addressing modes.

Other variants of the syntax are illustrated in the discussion on addressing modes. The use of condition codes for conditional and unconditional branching is explained in the section on syntactic sugar. In this example BRU W is assembled as BR W with condition code = 000.

Subroutine Call and Return

Syntax Example

JSR address JSR W Note that this can use all addressing modes.

RET RET The instruction does not take an argument.
RTI RTI Not yet implemented, this takes no argument.

Unary Register (These instructions use one source register, hence the name “unary”.)

Syntax Example

Op, Destination, Source, [Count] LLS %R5, %R6, 3
NOT %R2, %R1

The NOT operation does not take a count. The shift operations take a count, with the shift count defaulting to one if it is not provided. Shift by 0 is the same as a copy.

The restriction on this class of instruction is that the count, if used, must be a constant number known at the time that the assembler is run. As the registers are 32–bit, the counts are evaluated modulo 32. Constants and defined numbers are allowable in the instruction, but variables are not provided for in the syntax. Shifting by a count stored in a variable would be implemented using a looping structure.

A side effect of this constraint is that the right circular shift by a fixed amount may be translated by the assembler into an equivalent left circular shift.

Binary Register (These instructions use two source registers, hence the name “binary”)

Syntax Example

Op, Destination, Source_1, Source_2 ADD %R3, %R2, %R1

Note that the subtract operation is the only one for which the order of the source registers is important. SUB %R3, %R2, %R1 causes %R3 ¬ (%R2) – (%R1).

%R0 as a Source Register

Register %R0 is often used as a “source of 0”, a way to place the constant value 0 in another register or into a memory location.

%R0 as a Destination Register

Any operation that used register zero (%R0) as a destination in effect just discards the results. One use would be to force a arithmetic operation with the only goal of setting the sign bits.

As an example, we might say SUB %R0, %R1, %R2 to get the sign of (%R1) – (%R2) without storing the results of the subtraction.

Syntactic Sugar

Syntactic sugar, as applied to assembly language, refers to instructions that appear in the assembly language that are assembled as other instructions. This translation is performed by the assembler, which is the software program that emits the machine code. Our assembly language has a number of instructions that fall under this category. Here are some examples.

Syntactic Sugar Assembled As Comments

CLR %R2          LDI %R2, 0         Clears the register
CLW X            STR %R0, X         Clears the word at address X
INC %R2          ADI %R2, 1        Increments the register
DEC %R2          ADI %R2, -1        Decrements the register

NOP LLS %R0, %R0, 0 No-Operation: Does Nothing

RCS %R3, %R1, 3 LCS %R3, %R1, 13   Right circular shift by N is
                                    the same as left circular by
                                    32 – N. The shift count must
                                    be a constant number.

DBL %R2 LLS %R2, %R2, 1 Left shift by one is the
same as a multiply by 2.

MOV %R2, %R3 LSH %R2, %R3, 0 Shift by 0 is a copy.

NEG %R4, %R5 SUB %R4, %R0, %R5 Subtract from %R0 º 0 is
the same as negation.

TST %R1 SUB %R0, %R1, %R0 Compares %R1 to zero by

subtracting %R0 from it and
discarding the result.

CMP %R1, %R2     SUB %R0, %R1, %R2 Determines the sign of
                                    (%R1) – (%R2), discarding
                                    the result.

BRU BR 000 Branch always

BLT BR 001 Branch if negative
BEQ BR 010 Branch if zero

BLE              BR 011             Branch if not positive
BCO              BR 100             Branch if carry out is 0
BGE              BR 101             Branch if not negative
BNE              BR 110             Branch if not zero
BGT              BR 111             Branch if positive

BNS              BR 001             Same as BLT.
                                    Used by I/O operations, in
                                    which a negative status
                                    indicates an error.

More Comments on the Assembly Language

We now discuss the specifics of the syntax of the assembly language and show how the fields in the IR (Instruction Register) are used to specify the precise operation. The IR is a 32–bit register used to hold the instruction being executed.

This is a Load/Store RISC machine. Only Load Register and Store Register instructions access the memory. The only instructions that deal with memory addresses are the register load and store instructions, the branch (jump) instructions, and the subroutine call.

Immediate Addressing

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
Op–Code						Destination Register			Source Register			Immediate Argument

Op–Code        00000 NOP    Halt
                        00001 LDI     Load Immediate         (Does not use Source Register)
                        00010 ANDI Immediate logical AND
                        00011 ADDI Add Immediate

In these instructions, the source register most commonly will be the same as the destination register. While there is some benefit to having a distinct source register, the true motivation for this design is that it simplifies the logic of the control unit.

The most common immediate instructions will probably be the following.
                        LDI     %RD, 0                       -- Load the register with a 0.
                        LDI     %RD, 1                       -- Load the register with a 1
                        ADDI %RD, %RD,    1         -- Increment the register
                        ADDI %RD, %RD, – 1         -- Decrement the register

Input/Output Instructions
This design calls for isolated I/O, so it has dedicated input and output instructions.

Input

Op-Code 01000 GET Get a 32–bit word into a destination register from an input.

15 – 0

Destination
Register

Not Used

I/O

Address

Output

Op-Code 01001 PUT Put a 32–bit word from a source register to an output register.

15 – 0

Not Used

Source
Register

Not Used

I/O

Address

Note that these two instructions use different fields to denote the register affected. This choice will simplify the control circuit. All unused bits are assumed to be 0.

Memory Addressing

The next four instructions (LDR, STR, BR, and JSR) can use memory addressing. The first two use the memory address for a data copy between a specific register and memory. The next two use the memory address as the target location for a jump.

The generic structure of these instructions is as follows.

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
Op–Code					I bit	Register/Flags			Index			Address

The contents of bits 25 – 23 depends on the instruction.

The Real Reason for %R0 º 0

We now discuss an addressing trick that is one of the real reasons that we have included a general–purpose register that is identically 0. What we are doing is simplifying the control unit by not having to process non-indexed addressing; that is, direct or indirect. Note that bits 22 – 20 of the IR specify the index register to be used in address calculations.

When the I-bit (bit 26) is zero, we will call for indexed addressing, using the specified register. Thus the effective address is given by EA = Address + (%Rn), where %Rn is the register specified in bits 22 – 20 of the IR. But note the following
If Bits 22 – 20 = 0, we have %R0 and EA = Address + 0, thus a direct address.

When the I-bit is 1, we have the same convention. Indexed by %R0, we have indirect addressing, and indexed by another register, we have indexed-indirect addressing.

The “bottom line” on these addresses is shown in the table below.

	IR_22-20 = 000	IR_22-20 ¹ 000
IR₂₆ = 0	Indexed by %R0 (Direct)	Indexed
IR₂₆ = 1	Indirect, indexed by %R0 (Indirect)	Indexed-Indirect

Load Register

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
0	1	1	0	0	I bit	Destination Register			Index Register			Address

Here the I bit can be considered part of the opcode, if desired.
011000 Load the register using direct or indexed addressing
011001 Load the register using indirect or indexed-indirect addressing

For a load register operation, bits 25 – 23 specify the destination register. If the destination register is %R0, no register will change value. While this seems to be a “no operation”, it does set the condition codes in the PSR and might be used solely for that effect.

Store Register

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
0	1	1	0	1	I bit	Source Register			Index Register			Address

For a store register operation, bits 25 – 23 specify the source register. If the source register is %R0, the memory at the effective address will be cleared.

Subroutine Call

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
0	1	1	1	0	I bit	Not Used			Index Register			Address

Branch

31	30	29	28	27	26	25	24	23	22	21	20	19 – 0
0	1	1	1	1	I bit	Branch Condition			Index Register			Address

The condition code field determines under which conditions the Branch instruction is executed. The eight possible options are.

                         Condition                Action
                              000                     Branch Always                    (Unconditional Jump)
                              001                     Branch on negative result
                              010                     Branch on zero result
                              011                     Branch if result not positive
                              100                     Branch if carry-out is 0
                              101                     Branch if result not negative
                              110                     Branch if result is not zero
                              111                     Branch on positive result

Return from Subroutine / Return from Interrupt.

31	30	29	28	27	26 – 0
Op–Code					Not Used

Op–Code = 01010 RET Return from Subroutine
01011 RTI Return from Interrupt (Not presently implemented)

Neither of these instructions takes an argument or uses an address, as the appropriate information is assumed to have been placed on the stack.

Register-to-Register Instructions

Unary Register-To-Register

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14 – 0
Op Code						Destination Register			Source Register			Shift Count					Not Used

Opcode =        10000        LLS                 Logical Left Shift
                        10001        LCS                 Circular Left Shift
                        10010        RLS                 Logical Right Shift
                        10011        RAS                Arithmetic Right Shift
                        10100        NOT                Logical NOT (Shift count ignored)

NOTES:          1.               If (Count Field) = 0, a shift operation becomes a register move.
                        2.               If (Source Register = 0), the operation becomes a clear.
                        3.               Circular right shifts are not supported, because they may be
                                          implemented using circular left shifts.
                        4.               The shift count, being a 5 bit number, has values 0 to 31 inclusive.

The last topic for discussion is the binary register-to-register operations. By “binary” we do not refer to binary arithmetic, but to arithmetic operators, such as addition; those take two arguments and produce one result.

Binary Register-To-Register

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16 – 0
Op Code						Destination Register			Source Register 1			Source Register 2			Not used

Opcode =        10101        ADD               Addition
                        10110        SUB                Subtraction
                        10111        AND               Logical AND

11000 OR Logical OR
11001 XOR Logical Exclusive OR

NOTES: Subtract with (Destination Register) = 0 becomes a compare to set condition codes.

The Other Op-Codes

The other op–codes are not implemented in this design. The reason is simply the fact that the above selection of op–codes suffices to make the points required for this text.

Wasted Space

The reader might notice the label “Not Used” for many of the fields in the above instructions. This is a clear indication that a CISC design, with varying instruction lengths would be more efficient in the use of memory. The reason chosen by this author for the uniform instruction length is similar to that chosen by most designers of RISC: simplicity. For the RISC designers, simplicity implies a more efficient design. For this author, simplicity means a design that is easier to describe. The Boz–7 is inherently inefficient.

A Word Of Caution to System Programmers

At this point in the chapter, we pause and present a cautionary tale in the form of a possible strategy for programming the Boz–7 computer. This example might seem ridiculous, except for the fact that something like it happened to Apple Computers, when the company expanded the address space of its Macintosh line of computers to a full 32 bits.

Suppose it is the goal of a systems programmer to provide a device handler, written as a subroutine, and thus invoked by a JSR instruction. The clever programmer will recall that only the 20 low order bits (represented by five hexadecimal digits) are used in forming addresses. More specifically, the upper twelve bits (three hex digits) are ignored.

In indirect addressing as used with subroutine calls, the argument contains the address of subroutine to be called. Specifically, the following instruction will cause the subroutine at address 0x12345 to be called.

JSR *Z with M[Z] = 0x12345.

To be more specific in the example, note that M[Z] = 0x00012345, as it is properly represented by eight hexadecimal digits. It is just that we suppress leading zeroes.

Now consider the instruction

JSR *Z with M[Z] = 0x13612345.

Because only the 20 low order bits are used in forming the address of the subroutine, this is equivalent to the previous example, with the subroutine at address 0x12345 being called. A clever programmer can make use of this, with code such as the following.

            LDR    %R1, Z                        // Get the address of the pointer into register 1.
            RLS     %R1, %R1, 20            // Shift out the address bits
            ANDI %R2, %R1, 0x7          // R2 now has three low order bits of R1
            RLS     %R1, %R1, 3              // Shift these bits out
            ANDI %R1, %R1, 0x3F        // Keep the six low order bits.

JSR *Z // Complete the subroutine jump.

Reading the code fragment above, one might see that R2 has a priority and R1 has a six–bit number that will serve as a set of security flags. Let’s trace the execution of this clever code.

            LDR    %R1, Z                        // %R1 = = 0x13612345
            RLS     %R1, %R1, 20            // %R1 = = 0x00000136
            ANDI %R2, %R1, 0x7          // %R2 = = 0x00000006
            RLS     %R1, %R1, 3              // %R1 = = 0x00000026
            ANDI %R1, %R1, 0x3F        // %R1 = = 0x00000026 = = 00100110₂.
            JSR      *Z                                // Complete the subroutine jump.

So we have been clever and coded the 32–bit word describing the subroutine with three entries: its 20–bit address, the priority with which it runs, and the security flags with which it runs. Now, what happens when we upgrade the system to run with true 32–bit addresses? The answer is that the operating system, being full of these tricks, must be rewritten completely. This is not an easy task. As mentioned above, such has actually happened.

Organization of the Memory Unit

The design of the Boz–7 uses a 32–bit data word and 32–bit instruction word. For memory reference instructions, the address is formed from a 20–bit address in the CPU converted to a 26–bit address by use of the 6–bit page register for the PSR associated with the program. The process of generating a logical memory address is shown in a figure, copied from earlier in this chapter.

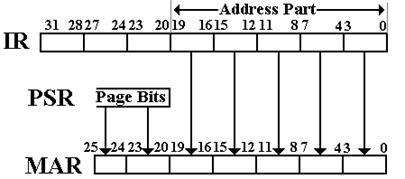
Figure: Memory Addressing in the Boz–7

Because the design uses a 26–bit address field to access memory, it was decided to have a memory requiring only 26 address bits; thus a memory with 64 Meg (2²⁶) of entries. Each data and instruction register of this computer contains 32 bits, so it was decided that each addressable memory unit would also contain 32 bits. Future revisions of this computer series might provide for byte addressing, but that has been postponed until this author can consider all of the consequence of providing such addressing. For now we keep it simple.

The Boz–7 Memory as It Is

The memory contains 2²⁶ ( 64M = 67,108,864 ) addressable 32–bit words. The memory is organized into sixty four logical banks, each holding 1M ( 1,048,576 ) 32–bit words.

The physical organization of the memory is based on memory chip technology that was current as of April, 2004. The memory uses eight Micron MT47H16M16 memory chips, each a chip being organized as a 16 Meg x 16 chip. These chips are organized into four memory banks, each bank containing a pair of 16 Meg x 16 chips and considered as a
16 Meg x 32 memory unit. Since this memory holds 2²⁶ addressable units, it must be accessed by twenty–six address lines; these are called A₂₅ .. A₀.

Low order interleaving is used. The 24 high–order bits of the address ( A₂₅ .. A₂ ) are sent to each of the memory banks and the 2 low–order bits of the address ( A₁, A₀ ) select the bank. To speed memory access, all memory accesses are made to four banks at once.

The data bus on this design is the only feature that stretches the current state-of-the-art in computer design. It is a 128–bit (four 32–bit word) bus, attached to the CPU via a 32KB SRAM cache with 128–bit cache lines. The organization is as follows.

Recalling that 32KB = 2¹⁵ bytes = 2¹⁸ bits, we see that the cache memory is divided into 1024 (2¹⁰) cache lines, each of 128 (2⁷) bits or eight 32–bit words, the same size as the data bus between cache memory and main memory. The goal is to transfer data one cache line at a time, facilitating fast access to main memory. We illustrate the cache in terms of reading from memory, such as might be done for fetching an instruction.

1) A 26–bit address is sent to the cache memory and READ is asserted.

2) If the addressed unit is in the cache memory, the 32–bit word is transmitted
to the MBR in the CPU within about 2-to-3 nanoseconds.

      3)   If the addressed unit is not in the cache memory, the 26–bit address is treated as
                        a)         A 3–bit offset within a cache line
                        b)         A 23–bit address associated with identifying the cache line

      4)   The 26–bit address is transmitted to the four–way interleaved memory, which
            sends the 24 high order bits of the address to all four memory banks. This results
            in the main memory producing four 32–bit words. These four words are
            transmitted simultaneously along the 128–bit data bus, filling the cache line.

5) The addressed word is then copied into the MBR of the CPU. With any luck, the
next few memory references will match entries in the cache.

Memory Interface

At this moment, the memory unit will have the following interface to the CPU
      MAR         the 20-bit Memory Address Register
      MBR         the 32–bit Memory Buffer Register
      READ       when asserted high, the CPU reads from memory
      WRITE     when asserted high, the CPU writes to memory

As an arbitrary tie breaker, we specify that READ takes precedence over WRITE, although the control unit should never assert the two signals at the same time. Thus, we have

READ	WRITE	Action
0	0	Nothing happens
0	1	CPU writes to memory
1	0	CPU reads from memory
1	1	CPU reads from memory

Solved Problems

1. Calculate the effective address for each of the following instructions. Assume that the contents of the index register 3 are (%R3) = – 7; W is the memory location 0x007D and that a partial memory map looks as follows:

Address	75	76	77	78	79	7A	7B	7C	7D	7E	7F	80	81	82
Contents	4D	7F	4F	BA	BA	77	8F	22	82	DD	E1	23	F0	0D

a) LDR, %R1 W . Remember that W refers to address 0x7D

b) BR * W . Remember that this is indirect addressing

c) BR * W, 3 . Handle this the way that the Boz-3b does

ANSWER:
      a)   Effective address is W, W = 0x7D.
      b)   Effective address is EA = M[W] = M[0x7D] = 0x82.
      c)   Pre-Indexed    EA = M[W + (%R3)] = M[0x7D – 7] = M[0x76] = 0x7F
            Post-Indexed EA = M[W] + (%R3) = M[0x7D] – 7 = 0x82 – 7 = 0x7B

2. In an assembly language program, the symbol Z refers to address 0x10B. The index register, R3, has value –4 (negative 4). The memory map (with 16–bit words) is:

Address	107	108	109	10A	10B	10C	10D
Contents	0113	0111	010F	010D	0108	0109	0107

What are the effective addresses for the following instructions:

a) Load Z Direct Addressing

b) Load * Z Indirect Addressing

c) Load Z, 3 Indexed Addressing.

d) Load * Z, 3 Indexed Indirect Addressing, Pre–Indexed

Answer:

a) The address is Z itself Z = = 0x10B.

b) The address is the contents of Z M[Z] = M[0x10B] = 0x108.

c) The address is Z + (R3) = 0x10B + (–4) = 0x10B – 4 = 0x107

d) The address is M[Z + (R3)] = M[0x10B – 4] = M[107] = 0x113.

3. Assemble the Boz–7 instruction LCS %R5, %R5, 9.
Show the machine language as eight hexadecimal digits.

ANSWER: The format of the instruction is as follows.

Unary Register-To-Register

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14 – 0
Op Code						Destination Register			Source Register			Shift Count					Not Used

The op code for this instruction is binary 10001 or hexadecimal 11.
The shift count is 0x9 or binary 1001.

NOTE: The shift count must be a 5–bit number to fill bits 19 – 16; it is 01001.

The binary version of the instruction is first written as follows

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14 – 0
10001					0	101			101			01001					0’s

Write this first as         10001 0 101 101 01001 00000
then group by fours     1000 1010 1101 0100 1000 00
which is really             1000 1010 1101 0100 1000 0000 0000 0000
or                                 0x8AD4 8000.

4. Assemble the Boz–5 instruction XOR %R6, %R2, %R4. Give the answer
as a hexadecimal number with eight hexadecimal digits.

ANSWER: The opcode for XOR is 0x19, or binary 11001.

The template for the object code for this type of instruction is as follows.

Binary Register-To-Register

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16 – 0
Op Code						Destination Register			Source 1			Source 2			Not used

XOR %R6, %R2, %R4 (Opcode is 11001)

16 – 0

Op Code

11001

Destination Register

110

Source 1

010

Source 2

100

Not used

Take the binary code and rearrange it left to right.

11001 0 110 010 100 0

1100 1011 0010 1000, which is 0xCB28 and expands to 0xCB28 0000.

5. Assemble the Boz–5 instruction ADD %R3, %R2, %R1.
Show the machine language as eight hexadecimal digits.

ANSWER: There are two possible answers to this one. I give both.
The opcode for ADD is 0x15 or 10101 in binary.

The binary register–to–register instruction format is as follows,
with color added to reduce confusion.

31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16 – 0
Op Code						Destination			Source 1			Source 2			Not used

The destination register is clearly %R3 (011). We have two options for the source registers.
Source 1 is %R1 (001) and source 2 is %R2 (010) or vice–versa.

Bits 15 – 0 of the word form 16 bits or four hexadecimal digits: 0X0000.
We now fill in bits 31 – 16, noting that each of bits 26 and 16 must be 0.

Option 1: Source 1 = 001, source 2 = 010

Bit	31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16
Binary	1	0	1	0	1	0	0	1	1	0	0	1	0	1	0	0
Hex	A				9				9				4

Option 1: Source 1 = 010, source 2 = 001

Bit	31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16
Binary	1	0	1	0	1	0	0	1	1	0	1	0	0	0	1	0
Hex	A				9				A				2

Append the four hexadecimal zeroes to either answer to get the following.

Answer 1: 0xA994 0000
Answer 2: 0xA9A2 0000

4. The page and offset addressing scheme of the Boz–7 series is described earlier in this chapter. Convert each of the page numbers and address offsets, given in hexadecimal to a full 26–bit address, also expressed in hexadecimal.

      a)   Page = 0X00               Offset = 0X00BAD
      b)   Page = 0X0A              Offset = 0X1CAFE
      c)   Page = 0X2F               Offset = 0X02030

ANSWER:
The address scheme prefixes two page bytes to the five bytes of address.
Note: The page number is a six–bit number, so the maximum page number is 0x3F.

a) Page = 0x00, Offset = 0x00BAD 00 00BAD or 000 0BAD

b) Page = 0x0A, Offset = 0x1CAFE 0A 1CAFE or 0A1 CAFE

c) Page = 0x2F, Offset = 0x02030 2F 02030 or 2F0 2030