Parallel Processing

Linear Speedup

Consider a computing system with N processors, possibly independent. Let C(N) be the cost of the N–processor system, with C₁ = C(1) being the cost of one processor. Normally, we assume that C(N) » N·C₁, that the cost of the system scales up approximately as fast as the number of processors. Let P(N) be the performance of the N–processor system, measured in some conventional measure such as MFLOPS (Million Floating Operations Per Second), MIPS (Million Instructions per Second), or some similar terms.

Let P₁ = P(1) be the performance of a single processor system on the same measure. The goal of any parallel processor system is linear speedup: P(N) » N·P₁. More properly, the actual goal is [P(N)/P₁] » [C(N)/C₁]. Define the speedup factor as S(N) = [P(N)/P₁]. The goal is S(N) » N.

Recall the pessimistic estimates from the early days of the supercomputer era that for large values we have S(N) < [N / log₂(N)], which is not an encouraging number.

N	100	1000	10,000	100,000	1,000,000
Maximum S(N)	15	100	753	6,021	30,172

It may be that it was these values that slowed the development of parallel processors. This is certainly one of the factors that lead Seymour Cray to make his joke comparing two strong oxen to 1,024 chickens (see the previous chapter for the quote).

The goal of parallel execution system design is called “linear speedup”, in which the performance of an N–processor system is approximately N times that of a single processor system. Fortunately, there are many problem types amenable to algorithms that can be caused to exhibit nearly linear speedup.

Linear Speedup: The View from the Early 1990’s

Here is what Harold Stone [R109] said in his textbook. The first thing to note is that he uses the term “peak performance” for what we call “linear speedup”. His definition of peak performance is quite specific. I quote it here.

“When a multiprocessor is operating at peak performance, all processors are engaged in useful work. No processor is idle, and no processor is executing an instruction that would not be executed if the same algorithm were executing on a single processor. In this state of peak performance, all N processors are contributing to effective performance, and the processing rate is increased by a factor of N. Peak performance is a very special state that
is rarely achievable.” [R109].

Stone notes a number of factors that introduce inefficiencies and inhibit peak performance.

1. The delays introduced by inter–processor communication.

2. The overhead in synchronizing the work of one processor with another.

3. The possibility that one or more processors will run out of tasks and do nothing.

4. The process cost of controlling the system and scheduling the tasks.

Motivations for Multiprocessing

Recalling the history of the late 1980’s and early 1990’s, we note that originally there was little enthusiasm for multiprocessing. At that time, it was thought that the upper limit on processor count in a serious computer would be either 8 or 16. This was a result of reflections on Amdahl’s Law, to be discussed in the next section of this chapter.

In the 1990’s, experiments at Los Alamos and Sandia showed the feasibility of multiprocessor systems with a few thousand commodity CPUs. As of early 2010, the champion processor was the Jaguar, a Cray XT5. It had a peak performance of 2.5 petaflops (2.5·10¹⁵ floating point operations per second) and a sustained performance in excess of 1.0 petaflop. As of mid–2011, the Jaguar is no longer the champion.

Multiprocessing is designed and intended to facilitate parallel processing. Remember that there are several classes of parallelism, only one of which presents a significant challenge to the computer system designer. Job–level parallelism or process–level parallelism uses multiple processors to run multiple independent programs simultaneously. As these programs do not communicate with each other, the design of systems to support this class
of programs presents very little challenge.

The true challenge arises with what might be called a parallel processing program, in which a single program executes on multiple processors. In this definition is the assumption that there must be some interdependencies between the multiple execution units. In this set of lectures, we shall focus on designs for efficient execution of solutions to large single software problems, such as weather forecasting, fluid flow modeling, and so on.

Most of the rest of this chapter will focus on what might be called “true parallel processing.”

Amdahl’s Law

Here is a variant of Amdahl’s Law that addresses the speedup due to N processors.

Let T(N) be the time to execute the program on N processors, with
T₁ = T(1) be the time to execute the program on 1 processor.

The speedup factor is obviously S(N) = T(1) / T(N). We consider any program as having two distinct components: the code that can be sped up by parallel processing, and the code that is essentially serialized. Assume that the fraction of the code that can be sped up is denoted by variable X. The time to execute the code on a single processor can be written as follows: T(1) = X·T₁ + (1 – X)·T₁ = T₁

Amdahl’s Law states that the time on an N–processor system will be
T(N) = (X·T₁)/N + (1 – X)·T₁ = [(X/N) + (1 – X)]·T₁

The speedup is S(N) = T(1) / T(N) = 1 / [(X / N) + (1 – X)]

It is easy to show that S(N) = N if and only if X = 1.0; there is no part of the code that is essentially sequential in nature and cannot be run in parallel. Let’s examine the two most interesting cases. Suppose that X = 1. Then S(N) = 1 / [ 1/N + 0] = 1 / [1/N] = N. Suppose that X = 0.0, then S(N) = 1 / [0/N + 1] = 1/1 = 1; no speedup.

Suppose that 0.0 < X < 1.0. Then [(X / N) + (1 – X)] > (1 – X) and 1 / [(X / N) + (1 – X)] is less than 1 / (1 – X). So we have the maximum speedup for 0.0 < X < 1.0; it is 1 / (1 – X).

Some Results Due to Amdahl’s Law

Here are some results on speedup as a function of number of processors.

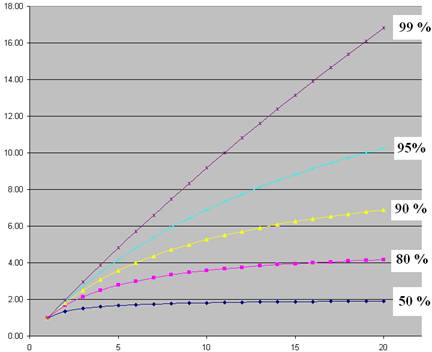
Description: "ô

Note that even 5% purely sequential code really slows things down. For much larger processor counts, the results are about the same.

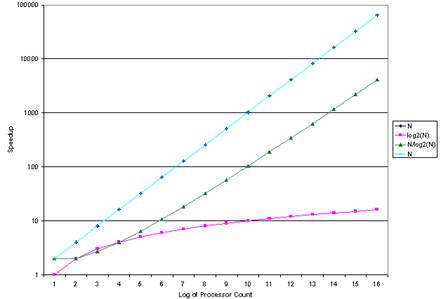
Description: э°

In the 1980’s and early 1990’s, the N/log₂(N) was thought to be the most likely speedup , with log₂(N) a second candidate. Each of these was discouraging. For N/log₂(N) speedup, S(1024) = 102 and S(65536) = 4096. For log₂(N) speedup, S(1024) = 10 and S(65536) = 16. Who would want to pay 65,536 times the dollars for 16 times the performance?

Flynn’s Taxonomy

Taxonomy is just a way of organizing items that are to be studied. Here is the taxonomy of computer designs developed by Michael Flynn, who published it in 1966.

		Data Streams
		Single	Multiple
Instruction Streams	Single	SISD (Standard computer)	SIMD (SSE on x86)
Instruction Streams	Multiple	MISD (No examples)	MIMD (Parallel processing)

The classification focuses on two of the more characterizations of processing: the nature of the data streams and the number of processors applied to those data streams. The simplest, of course, is the SISD design, which characterizes most computers. In this design, a single CPU is applied to processing a single data stream. This is the classic von Neumann architecture studied in the previous chapters of this textbook. Even if the processor incorporates internal parallelism, it would be characterized as SISD. Note that this class includes some processors of significant speed.

The two multiple–data–stream classifications, SIMD and MIMD, achieve speedup by processing multiple data streams at the same time. Each of these two classes will involve multiple processors, as a single processor can usually handle only one data stream. One difference between SIMD and MIMD is the number of control units. For SIMD, there is generally one control unit to handle fetching and decoding of the instructions. In the MIMD model, the computer has a number of processors possibly running independent programs. Two classes of MIMD, multiprocessors and multicomputers, will be discussed soon in this chapter. It is important to note that a MIMD design can be made to mimic a SIMD by providing the same program to all of its independent processors.

This taxonomy is still taught today, as it continues to be useful in characterizing
and analyzing computer architectures. However, this taxonomy has been replaced for serious design use because there are too many interesting cases that cannot be exactly fit into one of its classes. Note that it is very likely that Flynn included the MISD class just to be
complete. There is no evidence that a viable MISD computer was ever put to any real work.

Vector computers form the most interesting realization of SIMD architectures. This is especially true for the latest incarnation, called CUDA. The term “CUDA” stands for “Compute Unified Device Architecture”. The most noteworthy examples of the CUDA are produced by the NDIVIA Corporation (see www.nvidia.com). Originally NVIDIA focused on the production of GPUs (Graphical Processor Units), such as the NVIDIA GeForce 8800, which are high–performance graphic cards. It was found to be possible to apply a strange style of programming to these devices and cause them to function as general–purpose numerical processors. This lead to the evolution of a new type of device, which was released at CUDA by NVIDIA in 2007 [R68]. CUDA will be discussed in detail later.

SIMD vs. SPMD

Actually, CUDA machines such as the NVIDIA Tesla M2090 represent a variant of SIMD that is better called SPMD (Single Program Multiple Data). The difference between SIMD and SPMD is slight but important. The original SIMD architectures focused on amortizing the cost of a control unit over a number of processors by having a single CU control them all. This design leads to interesting performance problems, which are addressed by SPMD.

Parallel execution in the SIMD class involves all execution units responding to the same instruction at the same time. This instruction is associated with a single Program Counter that is shared by all processors in the system. Each execution unit has its own general purpose registers and allocation of shared memory, so SIMD does support multiple independent data streams. This works very well on looping program structures, but poorly in logic statements, such as if..then..else, case, or switch.

SIMD: Processing the “If statement”

Consider the following block of code, to be executed on four processors being run in SIMD mode. These are P0, P1, P2, and P3.

    if (x > 0) then
      y = y + 2 ;
    else
      y = y – 3;

Suppose that the x values are as follows (1, –3, 2, –4). Here is what happens.

Instruction	P0	P1	P2	P3
y = y + 2	y = y + 2	Nothing	y = y + 2	Nothing
y = y – 3	Nothing	y = y – 3	Nothing	y = y – 3

Execution units with data that do not fit the condition are disabled so that units with proper data may continue, causing inefficiencies. The SPMD avoids these as follows.

P0	P1	P2	P3
y = y + 2	y = y – 3	y = y + 2	y = y – 3

SIMD vs. SPMD vs. MIMD

The following figure illustrates the main difference between the SIMD and SPMD architectures and compares each to the MIMD architecture.

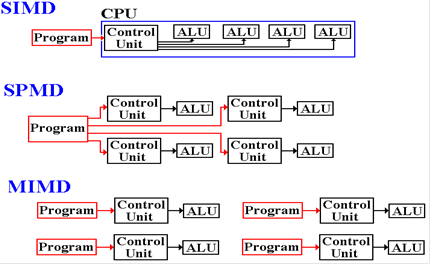
In a way, SPMD is equivalent to MIMD in which each processor is running the same high–level program. This does not imply running the exact same instruction stream, as data conditionals may differ between processors.

Multiprocessors, Multicomputers, and Clusters

We shall now investigate a number of strategies for parallel computing, focusing on MIMD. The two main classes of SIMD are vector processors and array processors. We have already discussed each, but will mention them again just to be complete.

There are two main classes of MIMD architectures [R15]:

a) Multiprocessors, which appear to have a shared memory and a shared address space.

b) Multicomputers, which comprise a large number of independent processors
(each with its own memory) that communicate via a dedicated network.

Note that each of the SIMD and MIMD architectures call for multiple independent
processors. The main difference lies in the instruction stream. SIMD architectures comprise a number of processors, each executing the same set of instructions (often in lock step). MIMD architectures comprise a number of processors, each executing its own program.
It may be the case that a number are executing the same program; it is not required.

Overview of Parallel Processing

Early on, it was discovered that the design of a parallel processing system is far from trivial if one wants reasonable performance. In order to achieve reasonable performance, one must address a number of important questions.

1. How do the parallel processors share data?

2. How do the parallel processors coordinate their computing schedules?

3. How many processors should be used?

4. What is the minimum speedup S(N) acceptable for N processors?
What are the factors that drive this decision?

In addition to the above question, there is the important one of matching the problem to the processing architecture. Put another way, the questions above must be answered within the context of the problem to be solved. For some hard real time problems (such as anti–aircraft defense), there might be a minimum speedup that needs to be achieved without regard to cost. Commercial problems rarely show this dependence on a specific performance level.

Sharing Data

There are two main categories here, each having subcategories.

Multiprocessors are computing systems in which all programs share a single address space. This may be achieved by use of a single memory or a collection of memory modules that are closely connected and addressable as a single unit. All programs running on such a system communicate via shared variables in memory. There are two major variants of multiprocessors: UMA and NUMA.

In UMA (Uniform Memory Access) multiprocessors, often called SMP (Symmetric Multiprocessors), each processor takes the same amount of time to access every
memory location. This property may be enforced by use of memory delays.

In NUMA (Non–Uniform Memory Access) multiprocessors, some memory accesses are faster than others. This model presents interesting challenges to the programmer in that race conditions become a real possibility, but offers increased performance.

Multicomputers are computing systems in which a collection of processors, each with its private memory, communicate via some dedicated network. Programs communicate by use of specific send message and receive message primitives. There are 2 types of multicomputers: clusters and MPP (Massively Parallel Processors).

Coordination of Processes

Processes operating on parallel processors must be coordinated in order to insure proper access to data and avoid the “lost update” problem associated with stale data. In the stale data problem, a processor uses an old copy of a data item that has been updated. We must guarantee that each processor uses only “fresh data”. We shall address this issue
head–on when we address the cache coherency problem.

Classification of Parallel Processors

Here is a figure from Tanenbaum [R15]. It shows a taxonomy of parallel computers, including SIMD, MISD, and MIMD.

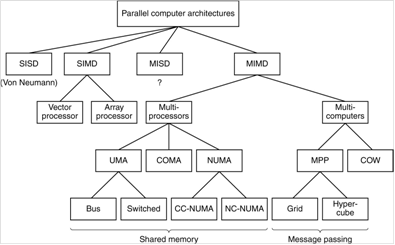
Note Tanenbaum’s sense of humor. What he elsewhere calls a cluster, he here calls a COW for Collection of Workstations. Here is another figure from Tanenbaum (Ref. 4, page 549). It shows a number of levels of parallelism including multiprocessors and multicomputers.

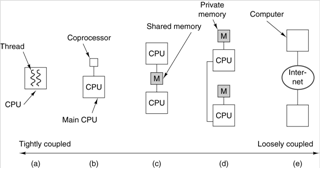
a) On–chip parallelism, b) An attached coprocessor (we shall discuss these soon),
c) A multiprocessor with shared memory, d) A multicomputer, each processor having
its private memory and cache, and e) A grid, which is a loosely coupled multicomputer.

Task Granularity

This is a model discussed by Harold Stone [R109]. It is formulated in terms of a time–sharing model of computation. In time sharing, each process that is active on a computer is given a fixed time allocation, called a quantum, during which it can use the CPU. At the end of its quantum, it is timed out, and another process is given the CPU. The Operating System will move the place a reference to the timed–out process on a ready queue and restart it a bit later. This model does not account for a process requesting I/O and not being able to use its entire quantum due to being blocked.

Let R be the length of the run–time quantum, measured in any convenient time unit. Typical values are 10 to 100 milliseconds (0.01 to 0.10 seconds). Let C be the amount of time during that run–time quantum that the process spends in communication with other processes. The applicable ratio is (R/C), which is defined only for 0 < C £ R.

In course–grain parallelism, R/C is fairly high so that computation is efficient.

In fine–grain parallelism, R/C is low and little work gets done due to the excessive overhead of communication and coordination among processors.

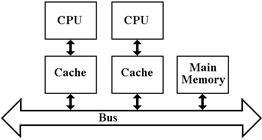
UMA Symmetric Multiprocessor Architectures

Beginning in the later 1980’s, it was discovered that several microprocessors can be usefully placed on a bus. We note immediately that, though the single–bus SMP architecture is easier to program, bus contention places an upper limit on the number of processors that can be attached. Even with use of cache memory for each processor to cut bus traffic, this upper limit seems to be about 32 processors [R15]. Here is a depiction of three classes of bus–based UMA architectures: a) No caching, and two variants of individual processors with caches: b) Just cache memory, and c) Both cache memory and a private memory.

In each architecture, there is a global memory shared by all processors. The bus structure is not the only way to connect a number of processors to a number of shared memories. Here are two others: the crossbar switch and the omega switch. These are properly the subject of a more advanced course, so we shall have little to say about them here.

The basic idea behind the crossbar and the omega is efficient communication among units that form part of the computer. A typical unit can be a CPU with an attached cache, or a memory bank. It is likely the case that there is little memory–to–memory communication.

The figure above shows three distinct UMA architectures. The big issue in each of these is the proper sharing of items found in a common global memory. For that reason, we do not consider the third option (cache memory and private memory), as data stored only in private memories cannot cause problems. We ignore the first option (no cache, just direct connect to the global memory) because it is too slow and also because it causes no problems. The only situation that causes problems is the one with a private cache for each CPU.

Cache Coherency

A parallel processing computer comprises a number of independent processors connected by a communications medium, either a bus or more advanced switching system, such as a crossbar switch. We focus this discussion on multiprocessors, which use a common main memory as the primary means for inter–processor communication. Later, we shall see that many of the same issues appear for multicomputers, which are more loosely coupled.

A big issue with the realization of the shared–memory multiprocessors was the development of protocols to maintain cache coherency. Briefly put, this insures that the value in any individual processor’s cache is the most current value and not stale data. Ideally, each processor in a multiprocessor system will have its own “chunk of the problem”, referencing data that are not used by other processors. Cache coherency is not a problem in that case as the individual processors do not share data. We shall see some situations in which this partitioning of data can be achieved, but these are not common.

In real multiprocessor systems, there are data that must be shared between the individual processors. The amount of shared data is usually so large that a single bus would be overloaded were it not that each processor had its own cache. When an individual processor accesses a block from the shared memory, that block is copied into that processors cache. There is no problem as long as the processor only reads the cache. As soon as the processor writes to the cache, we have a cache coherency problem. Other processors accessing those data might get stale copies. One logical way to avoid this process is to implement each individual processor’s cache using the write–through strategy. In this strategy, the shared memory is updated as soon as the cache is updated. Naturally, this increases bus traffic significantly. Reduction of bus traffic is a major design goal.

Logically speaking, it would be better to do without cache memory. Such a solution would completely avoid the problems of cache coherency and stale data. Unfortunately, such a solution would place a severe burden on the communications medium, thereby limiting the number of independent processors in the system. This section will focus on a common bus as a communications medium, but only because a bus is easier to draw. The same issues apply to other switching systems.

The Cache Write Problem

Almost all problems with cache memory arise from the fact that the processors write data to the caches. This is a necessary requirement for a stored program computer. The problem in uniprocessors is quite simple. If the cache is updated, the main memory must be updated at some point so that the changes can be made permanent.

Description: "Ð

It was in this context that we first met the issue of cache write strategies. We focused on two strategies: write–through and write–back. In the write–through strategy, all changes to the cache memory were immediately copied to the main memory. In this simpler strategy, memory writes could be slow. In the write–back strategy, changes to the cache were not propagated back to the main memory until necessary in order to save the data. This is more complex, but faster.

The uniprocessor issue continues to apply, but here we face a bigger problem.

Description: "Ð

The coherency problem arises from the fact that the same block of the shared main memory may be resident in two or more of the independent caches. There is no problem with reading shared data. As soon as one processor writes to a cache block that is found in another processor’s cache, the possibility of a problem arises.

We first note that this problem is not unique to parallel processing systems. Those students who have experience with database design will note the strong resemblance to the “lost update” problem. Those with experience in operating system design might find a hint of the theoretical problem called “readers and writers”. It is all the same problem: handling the issues of inconsistent and stale data. The cache coherency problems and strategies for solution are well illustrated on a two processor system. We shall consider two processors P1 and P2, each with a cache. Access to a cache by a processor involves one of two processes: read and write. Each process can have two results: a cache hit or a cache miss.

Recall that a cache hit occurs when the processor accesses its private cache and finds the addressed item already in the cache. Otherwise, the access is a cache miss. Read hits occur when the individual processor attempts to read a data item from its private cache and finds it there. There is no problem with this access, no matter how many other private caches contain the data. The problem of processor receiving stale data on a read hit, due to updates by other independent processors, is handled by the cache write protocols.

Cache Coherency: The Wandering Process Problem

This strange little problem was much discussed in the 1980’s (Ref. 3), and remains somewhat of an issue today. Its lesser importance now is probably due to revisions in operating systems to better assign processes to individual processors in the system. The problem arises in a time–sharing environment and is really quite simple. Suppose a dual–processor system: CPU_1 with cache C_1 and CPU_2 with cache C_2. Suppose a process P that uses data to which it has exclusive access. Consider the following scenario:

1. The process P runs on CPU_1 and accesses its data through the cache C_1.

2. The process P exceeds its time quantum and times out.
All dirty cache lines are written back to the shared main memory.

3. After some time, the process P is assigned to CPU_2. It accesses its data
through cache C_2, updating some of the data.

4. Again, the process P times out. Dirty cache lines are written back to the memory.

5. Process P is assigned to CPU_1 and attempts to access its data. The cache C_1
retains some data from the previous execution, though those data are stale.

In order to avoid the problem of cache hits on stale data, the operating system must flush every cache line associated with a process that times out or is blocked.

Cache Coherency: Snoop Tags

Each line in a cache is identified by a cache tag (block number), which allows the determination of the primary memory address associated with each element in the cache. Cache blocks are identified and referenced by their memory tags.

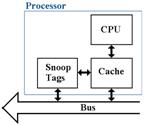
Description: "Ø

In order to maintain coherency, each individual cache must monitor the traffic in cache tags, which corresponds to the blocks being read from and written to the shared primary memory. This is done by a snooping cache (or snoopy cache, after the Peanuts comic strip), which is just another port into the cache memory from the shared bus. The function of the snooping cache is to “snoop the bus”, watching for references to memory blocks that have copies in the associated data cache.

Cache Coherency: A Simple Protocol

We begin our consideration of a simple cache coherency protocol. After a few comments on this, we then move to consideration of the MESI protocol. In this simple protocol, each block in the cache of an individual processor can be in one of three states:

1. Invalid: the cache block does not contain valid data. This might indicate that the
data in the cache are stale.

      2.   Shared (Read Only): the cache block contains valid data, loaded as a result of a
            read request. The processor has not written to it; it is “clean” in that it is not “dirty”
            (been changed). This cache block may be shared with other processors; it may
            be present in a number of individual processor caches.

      3.   Modified (Read/Write): the cache block contains valid data, loaded as a result of
            either a read or write request. The cache block is “dirty” because its individual
            processor has written to it. It may not be shared with other individual processors,
            as those other caches will contain stale data.

A First Look at the Simple Protocol

Let’s consider transactions on the cache when the state is best labeled as “Invalid”. The requested block is not in the individual cache, so the only possible transitions correspond to misses, either read misses or write misses.

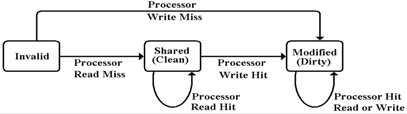
Note that this process cannot proceed if another processor’s cache has the block labeled as “Modified”. We shall discuss the details of this case later. In a read miss, the individual processor acquires the bus and requests the block. When the block is read into the cache, it is labeled as “not dirty” and the read proceeds.

In a write miss, the individual processor acquires the bus, requests the block, and then writes data to its copy in the cache. This sets the dirty bit on the cache block. Note that the processing of a write miss exactly follows the sequence that would be followed for a read miss followed by a write hit, referencing the block just read.

Cache Misses: Interaction with Other Processors

We have just established that, on either a read miss or a write miss, the individual processor must acquire the shared communication channel and request the block. If the requested block is not held by the cache of any other individual processor, the transition takes place as described above. We shall later add a special state to account for this possibility; that is the contribution of the MESI protocol.

If the requested block is held by another cache and that copy is labeled as “Modified”, then a sequence of actions must take place: 1) the modified copy is written back to the shared primary memory, 2) the requesting processor fetches the block just written back to the shared memory, and 3) both copies are labeled as “Shared”.

If the requested block is held by another cache and that copy is labeled as “Shared”, then the processing depends on the action. Processing a read miss only requires that the requesting processor fetch the block, mark it as “Shared”, and execute the read.

On a write miss, the requesting processor first fetches the requested block with the protocol responding properly to the read miss. At the point, there should be no copy of the block marked “Modified”. The requesting processor marks the copy in its cache as “Modified” and sends an invalidate signal to mark all copies in other caches as stale.

The protocol must insure that no more than one copy of a block is marked as “Modified”.

Write Hits and Misses

As we have noted above, the best way to view a write miss is to consider it as a sequence of events: first, a read miss that is properly handled, and then a write hit. This is due to the fact that the only way to handle a cache write properly is to be sure that the affected block has been read into memory. As a result of this two–step procedure for a write miss, we may propose a uniform approach that is based on proper handling of write hits.

At the beginning of the process, it is the case that no copy of the referenced block in the cache of any other individual processor is marked as “Modified”.

If the block in the cache of the requesting processor is marked as “Shared”, a write hit to it will cause the requesting processor to send out a “Cache Invalidate” signal to all other processors. Each of these other processors snoops the bus and responds to the Invalidate signal if it references a block held by that processor. The requesting processor then marks its cache copy as “Modified”.

If the block in the cache of the requesting processor is already marked as “Modified”, nothing special happens. The write takes place and the cache copy is updated.

The MESI Protocol

This is a commonly used cache coherency protocol. Its name is derived from the fours states in its FSM representation: Modified, Exclusive, Shared, and Invalid.

This description is taken from Section 8.3 of Tanenbaum [R15].

Each line in an individual processors cache can exist in one of the four following states:

1. Invalid The cache line does not contain valid data.

2. Shared Multiple caches may hold the line; the shared memory is up to date.

3. Exclusive No other cache holds a copy of this line;
the shared memory is up to date.

4. Modified The line in this cache is valid; no copies of the line exist in
other caches; the shared memory is not up to date.

The main purpose of the Exclusive state is to prevent the unnecessary broadcast of a Cache Invalidate signal on a write hit. This reduces traffic on a shared bus. Recall that a necessary precondition for a successful write hit on a line in the cache of a processor is that no other processor has that line with a label of Exclusive or Modified. As a result of a successful write hit on a cache line, that cache line is always marked as Modified.

Suppose a requesting processor processing a write hit on its cache. By definition, any copy of the line in the caches of other processors must be in the Shared State. What happens depends on the state of the cache in the requesting processor.

1. Modified The protocol does not specify an action for the processor.

2. Shared The processor writes the data, marks the cache line as Modified,
and broadcasts a Cache Invalidate signal to other processors.

3. Exclusive The processor writes the data and marks the cache line as Modified.

If a line in the cache of an individual processor is marked as “Modified” and another processor attempts to access the data copied into that cache line, the individual processor must signal “Dirty” and write the data back to the shared primary memory.

Consider the following scenario, in which processor P1 has a write miss on a cache line.

1. P1 fetches the block of memory into its cache line, writes to it, and marks it Dirty.

2. Another processor attempts to fetch the same block from the shared main memory.

3. P1’s snoop cache detects the memory request. P1 broadcasts a message “Dirty” on
the shared bus, causing the other processor to abandon its memory fetch.

4. P1 writes the block back to the share memory and the other processor can access it.

Events in the MESI Protocol

There are six events that are basic to the MESI protocol, three due to the local processor and three due to bus signals from remote processors [R110].

Local Read The individual processor reads from its cache memory.

Local Write The individual processor writes data to its cache memory.

Local Eviction The individual processor must write back a dirty line from its
cache in order to free up a cache line for a newly requested block.

Bus Read           Another processor issues a read request to the shared primary
                           memory for a block that is held in this processors individual cache.
                           This processor’s snoop cache detects the request.

Bus Write Another processor issues a write request to the shared primary
memory for a block that is held in this processors individual cache.

Bus Upgrade      Another processor signals that a write to a cache line that is shared
                           with this processor. The other processor will upgrade the status of
                           the cache line from “Shared” to “Modified”.

The MESI FSM: Action and Next State (NS)

Here is a tabular representation of the Finite State Machine for the MESI protocol.
Depending on its Present State (PS), an individual processor responds to events.

Local Read

Local

Write

Local

Eviction

Bus Read

Bus Write

BU – Bus

Upgrade

I Invalid

Issue BR
Do other caches have this line.

Yes: NS = S

No: NS = E

Issue BW

NS = M

NS = I

nothing

Shared

Do nothing

Issue BU
NS = M

NS = I

Respond

Shared

NS = I

E Exclusive

Do nothing

NS = M

NS = I

Respond Shared

NS = S

NS = I

Error

Should not occur.

M Modified

Do nothing

nothing

Write data back.

NS = I.

Respond Dirty.

Write data back

NS = S

Respond Dirty.

Write data back

NS = I

Error

Should not occur.

MESI Illustrated

Here is an example from the text by Andrew Tanenbaum [R15]. This describes three individual processors, each with a private cache, attached to a shared primary memory. When the multiprocessor is turned on, all cache lines are marked invalid. We begin
with CPU reading block A from the shared memory.

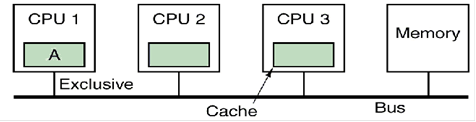
CPU 1 is the first (and only) processor to request block A from the shared memory. It issues a BR (Bus Read) for the block and gets its copy. The cache line containing block A is marked Exclusive. Subsequent reads to this block access the cached entry and not the shared memory.Neither CPU 2 nor CPU 3 respond to the BR.

We now assume that CPU 2 requests the same block. The snoop cache on CPU 1 notes the request and CPU 1 broadcasts “Shared”, announcing that it has a copy of the block.

Both copies of the block are marked as shared. This indicates that the block is in two or more caches for reading and that the copy in the shared primary memory is up to date.
CPU 3 does not respond to the BR. At this point, either CPU 1 or CPU 2 can issue a local write, as that step is valid for either the Shared or Exclusive state. Both are in the Shared state. Suppose that CPU 2 writes to the cache line it is holding in its cache. It issues a BU (Bus Upgrade) broadcast, marks the cache line as Modified, and writes the data to the line.

CPU 1 responds to the BU by marking the copy in its cache line as Invalid.

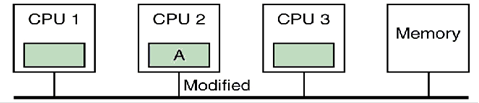
CPU 3 does not respond to the BU. Informally, CPU 2 can be said to “own the cache line”.

Now suppose that CPU 3 attempts to read block A from primary memory. For CPU 1, the cache line holding that block has been marked as Invalid. CPU 1 does not respond to the BR (Bus Read) request. CPU 2 has the cache line marked as Modified. It asserts the signal “Dirty” on the bus, writes the data in the cache line back to the shared memory, and marks the line “Shared”. Informally, CPU 2 asks CPU 3 to wait while it writes back the contents of its modified cache line to the shared primary memory. CPU 3 waits and then gets a correct copy. The cache line in each of CPU 2 and CPU 3 is marked as Shared.

Summary

We have considered cache memories in parallel computers, both multiprocessors and multicomputers. Each of these architectures comprises a number of individual processors with private caches and possibly private memories. We have noted that the assignment of a private cache to each of the individual processors in such architecture is necessary if we are to get acceptable performance. We have noted that the major issue to consider in these designs is that of cache coherency. Logically speaking, each of the individual processors must function as if it were accessing the one and only copy of the memory block, which resides in the shared primary memory.

We have proposed a modern solution, called MESI, which is a protocol in the class called “Cache Invalidate”. This shows reasonable efficiency in the maintenance of coherency.

The only other class of protocols falls under the name “Central Database”. In this, the shared primary memory maintains a list of “which processor has which block”. This centralized management of coherency has been shown to place an unacceptably high processing load on the shared primary memory. For this reason, it is no longer used.

Loosely Coupled Multiprocessors

Our previous discussions of multiprocessors focused on systems built with a modest number of processors (no more than about 50), which communicate via a shared bus. The class of computers we shall consider now is called “MPP”, for Massively Parallel Processor”. As we shall see, the development of MPP systems was resisted for a long time, due to the belief that such designs could not be cost effective. We shall see that MPP systems finally evolved due to a number of factors, at least one of which only became operative in the late 1990’s.

1. The availability of small and inexpensive microprocessor units (Intel 80386, etc.)
that could be efficiently packaged into a small unit.

2. The discovery that many very important problems were quite amenable to
parallel implementation.

3.         The discovery that many of these important problems had structures of such
            regularity that sequential code could be automatically translated for parallel
            execution with little loss in efficiency.

Early History: The C.mmp

While this chapter will focus on multicomputers, it is instructive to begin with a review of a paper on the C.mmp, which is a shared–memory multiprocessor developed at Carnegie Mellon University in the early 1970’s. The C.mmp is described in a paper by Wulf and Harbinson [R111], which has been noted as “one of the most thorough and balanced research–project retrospectives … ever seen”. Remarkably, this paper gives a thorough description of the project’s failures.

The C.mmp is described [R111] as “a multiprocessor composed of 16 PDP–11’s, 16 independent memory banks, a crosspoint [crossbar] switch which permits any processor to access any memory, and a typical complement of I/O equipment”. It includes an independent bus, called the “IP bus”, used to communicate control signals.

As of 1978, the system included the following 16 processors.

5 PDP–11/20’s, each rated at 0.20 MIPS (that is 200,000 instructions per second)

11 PDP–11/40’s, each rated at 0.40 MIPS

3 megabytes of shared memory (650 nsec core and 300 nsec semiconductor)

The system was observed to compute at 6 MIPS.

The Design Goals of the C.mmp

The goal of the project seems to have been the construction of a simple system using as many commercially available components as possible. The C.mmp was intended to be a research project not only in distributed processors, but also in distributed software. The native operating system designed for the C.mmp was called “Hydra”. It was intended as an OS kernel, intended to provide only minimal services and encourage experimentation in system software. As of 1978, the software developed on top of the Hydra kernel included file systems, directory systems, schedulers and a number of language processors.

Another part of the project involved the development of performance evaluation tools, including the Hardware Monitor for recording the signals on the PDP–11 data bus and software tools for analyzing the performance traces. One of the more important software tools was the Kernel Tracer, which was built into the Hydra kernel. It allowed selected operating system events, such as context swaps and blocking on semaphores, to be recorded while a set of applications was running. The Hydra kernel was originally designed based on some common assumptions. When experimentation showed these to be false, the Hydra kernel was redesigned.

The C.mmp: Lessons Learned

The researchers were able to implement the C.mmp as “a cost–effective, symmetric multiprocessor” and distribute the Hydra kernel over all of the processors. The use of two variants of the PDP–11 was considered as a mistake, as it complicated the process of making the necessary processor and operating system modifications. The authors had used newer variants of the PDP–11 in order to gain speed, but concluded that “It would have been better to have had a single processor model, regardless of speed”. The critical component was expected to be the crossbar switch. Experience showed the switch to be “very reliable, and fast enough”. Early expectations that the “raw speed” of the switch would be important were not supported by experience.

The authors concluded that “most applications are sped up by decomposing their algorithms to use the multiprocessor structure, not by executing on processors with short memory access times”. The simplicity of the Hydra kernel, with much system software built on top of it, yielded benefits, such as few software errors caused by inadequate synchronization.

The C.mmp: More Lessons Learned

Here I quote from Wulf & Harbison [R111], arranging their comments in an order not found in their original. The PDP–11 was a memory–mapped architecture with a single bus, called the UNIBUS, that connected the CPU to both memory and I/O devices.

      1.   “Hardware (un)reliability was our largest day–to–day disappointment … The
            aggregate mean–time–between–failure (MTBF) of C.mmp/Hydra fluctuated
            between two to six hours.”

2. “About two–thirds of the failures were directly attributable to hardware problems.
There is insufficient fault detection built into the hardware.”

3. “We found the PDP–11 UNIBUS to be especially noisy and error–prone.”

4. “The crosspoint [crossbar] switch is too trusting of other components; it can be
hung by malfunctioning memories or processors.”

My favorite lesson learned is summarized in the following two paragraphs in the report.

“We made a serious error in not writing good diagnostics for the hardware. The software developers should have written such programs for the hardware.”

“In our experience, diagnostics written by the hardware group often did not test components under the type of load generated by Hydra, resulting in much finger–pointing between groups.”

The Challenge for Multiprocessors

As multicore processors evolve into manycore processors (with a few hundreds of cores), the challenge remains the same as it always has been. The goal is to get an increase in computing power (or performance or whatever) that is proportional to the cost of providing a large number of processors. The design problems associated with multicore processors remain the same as they have always been: how to coordinate the work of a large number of computing units so that each is doing useful work. These problems generally do not arise when the computer is processing a number of independent jobs that do not need to communicate. The main part of these design problems is management of access to shared memory. This part has two aspects:

      1.   The cache coherency problem, discussed earlier.
      2.   The problem of process synchronization, requiring the use of lock
            variables, and reliable processes to lock and unlock these variables.

Task Management in Multicomputers

The basic idea behind both multicomputers and multiprocessors is to run multiple tasks or multiple task threads at the same time. This goal leads to a number of requirements, especially since it is commonly assumed that any user program will be able to spawn a number of independently executing tasks or processes or threads.

According to Baron and Higbie [R112], any multicomputer or multiprocessor system must provide facilities for these five task–management capabilities.

1. Initiation A process must be able to spawn another process;
that is, generate another process and activate it.

2. Synchronization A process must be able to suspend itself or another process
until some sort of external synchronizing event occurs.

3. Exclusion A process must be able to monopolize a shared resource,
such as data or code, to prevent “lost updates”.

4. Communication A process must be able to exchange messages with any
other active process that is executing on the system.

5. Termination A process must be able to terminate itself and release
all resources being used, without any memory leaks.

These facilities are more efficiently provided if there is sufficient hardware support.

Multiprocessors

One of the more common mechanisms for coordinating multiple processes in a single address space multiprocessor is called a lock. This feature is commonly used in databases accessed by multiple users, even those implemented on single processors.

Multicomputers

These must use explicit synchronization messages in order to coordinate the processes. One method is called “barrier synchronization”, in which there are logical spots, called “barriers” in each of the programs. When a process reaches a barrier, it stops processing and waits until it has received a message allowing it to proceed. The common idea is that each processor must wait at the barrier until every other processor has reached it. At that point every processor signals that it has reached the barrier and received the signal from every other processor. Then they all continue.

Other processors, such as the MIPS, implement a different mechanism.

A Naive Lock Mechanism and Its Problems

Consider a shared memory variable, called LOCK, used to control access to a specific shared resource. This simple variable has two values. When the variable has value 0, the lock is free and a process may set the lock value to 1 and obtain the resource. When the variable has value 1, the lock is unavailable and any process must wait to have access to the resource. Here is the simplistic code (written in Boz–7 assembly language) that is executed by any process to access the variable.

GETIT LDR %R1,LOCK LOAD THE LOCK VALUE INTO R1.

CMP %R1,%R0 IS THE VALUE 0? REMEMBER THAT
REGISTER R0 IS IDENTICALLY 0.

BGT GETIT NO, IT IS 1. TRY AGAIN.

LDI %R1,1 SET THE REGISTER TO VALUE 1

STR %R1,LOCK STORE VALUE OF 1, LOCKING IT

The Obvious Problem

We suppose a context switch after process 1 gets the lock and before it is able to write
the revised lock value back to main memory. It is a lost update.

Event Process 1 Process 2

LOCK = 0

LDR %R1,LOCK
%R1 has value 0

CMP %R1,%R0
Compares OK. Continue

Context switch LDR %R1,LOCK
%R1 has value 0

Set LOCK = 1
Continue

LOCK = 1
Context switch LDI %R1,1

STR %R1,LOCK

Continue

LOCK = 1
Each process has access to the resource and continues processing.

Hardware Support for Multitasking

Any processor or group of processors that supports multitasking will do so more efficiently if the hardware provides an appropriate primitive operation. A test–and–set operation with a binary semaphore (also called a “lock variable”) can be used for both mutual exclusion and process synchronization. This is best implemented as an atomic operation, which in this context is one that cannot be interrupted until it completes execution. It either executes completely or fails.

Atomic Synchronization Primitives

What is needed is an atomic operation, defined in the original sense of the word to be an operation that must complete once it begins. Specifically it cannot be interrupted or suspended by a context switch. There may be some problems associated with virtual memory, particularly arising from page faults. These are easily fixed. We consider an atomic instruction that is to be called CAS, standing for either Compare and Set, or
Compare and Swap

Either of these takes three arguments: a lock variable, an expected value (allowing the resource to be accessed) and an updated value (blocking access by other processes to this resource). Here is a sample of proper use.

LDR %R1,LOCK ATTEMPT ACCESS, POSSIBLY
CAUSING A PAGE FAULT

CAS LOCK,0,1 SET TO 1 TO LOCK IT.

Two Variants of CAS

Each variant is atomic; it is guaranteed to execute with no interrupts or
context switches. It is a single CPU instruction, directly executed by
the hardware.

Compare_and_set (X, expected_value, updated_value)

If (X == expected_value)

X ¬ updated_value

Return True

Else Return False

Compare_and_swap (X, expected_value, updated_value)

If (X == expected_value)

Swap X « updated_value

Return True

Else Return False

Such instructions date back at least to the IBM System/370 in 1970.

What About MESI?

Consider two processes executing on different processors, each with its own cache memory (probably both L1 and L2). Let these processes be called P1 and P2. Suppose that each P1 and P2 have the variable LOCK in cache memory and that each wants to set it.

Suppose P1 sets the lock first. This write to the cache block causes a cache invalidate to be broadcast to all other processes. The shared memory value of LOCK is updated and then copied to the cache associated with process P2. However, there is no signal to P2 that the value in its local registers has become invalid. P2 will just write a new value to its cache. In other words, the MESI protocol will maintain the integrity of values in shared memory. However, it cannot be used as a lock mechanism. Any synchronization primitives that we design will assume that the MESI protocol is functioning properly and add important functionality to it.

CAS: Implementation Problems

The single atomic CAS presents some problems in processor design, as it requires both a memory read and memory write in a single uninterruptable instruction. The option chosen by the designers of the MIPS is to create a pair of instructions in which the second instruction returns a value showing whether or not the two executed as if they were atomic. In the MIPS design, this pair of instructions is as follows:

LL Load Linked LL Register, Memory Address

SC Store Conditional SC Register, Memory Address

This code either fails or swaps the value in register $S4 with the value in
the memory location with address in register $S1.

TRY: ADD $T0,$0,$S4 MOVE VALUE IN $S4 TO REGISTER $T0

LL $T1,0($S1) LOAD $T1 FROM MEMORY ADDRESS

SC $T0,0($S1) STORE CONDITIONAL

BEQ $T0,$0,TRY BRANCH STORE FAILS, GO BACK

ADD $S4,$0,$T1 PUT VALUE INTO $S4

More on the MESI Issue

Basically the MESI protocol presents an efficient mechanism to handle the effects of processor writes to shared memory. MESI assumes a shared memory in which each addressable item has a unique memory address and hence a unique memory block number.

But note that the problem associated with MESI would largely go away if we could make one additional stipulation: once a block in shared memory is written by a processor, only that processor will access that block for some time. We shall see that a number of problems have this desirable property. We may assign multiple processors to the problem and enforce the following.

a) Each memory block can be read by any number of processors,
provided that it is only read.

b) Once a memory block is written to by one processor, it is the “sole property”
of that processor. No other processor may read or write that memory block.

Remember that a processor accesses a memory block through its copy in cache.

The High–End Graphics Coprocessor and CUDA

We now proceed to consider a type of Massively Parallel Processor and a class of problems well suited to be executed on processors of this class. The main reason for this match is the modification to MESI just suggested. In this class of problems, the data being processed can be split into small sets, with each set being assigned to one, and only one, processor. The original problems of this class were taken from the world of computer graphics and focused on rendering a digital scene on a computer screen. For this reason, the original work on the class of machines was done under the name GPU (Graphical Processing Unit). In the early development, these were nothing more than high performance graphic cards.

Since about 2003, the design approach taken by NVIDIA Corporation for these high end graphical processing units has been called “many–core” to distinguish it from the more traditional multicore designs found in many commercial personal computers. While a multicore CPU might have 8 to 16 cores, a many–core GPU will have hundreds of cores. In 2008, the NVIDIA GTX 280 GPU had 280 cores [R68]. In July 2011, the NVIDIA Tesla C2070 had 448 cores and 6 GB memory [R113].

The historic pressures on the designers of GPUs are well described by Kirk & Hwu [R68].

“The design philosophy of the GPUs is shaped by the fast growing video game industry, which exerts tremendous economic pressure for the ability to perform a massive number of floating–point calculations per video frame in advanced games. … The prevailing solution to date is to optimize for the execution throughput of massive numbers of threads. … As a result, much more chip area is dedicated to the floating–point calculations.”

“It should be clear now that GPUs are designed as numeric computing engines, and they will not perform well on some tasks on which CPUs are designed to perform well; therefore, one should expect that most applications will use both CPUs and GPUs, executing the sequential parts on the CPU and the numerically intensive parts on the GPUs. This is why the CUDA™ (Compute Unified Device Architecture) programming model, introduced by NVIDIA in 2007, is designed to support joint CPU/GPU execution of an application.”

Game Engines as Supercomputers

It may surprise students to learn that many of these high–end graphics processors are actually export controlled as munitions. In this case, the control is due to the possibility of using these processors as high–performance computers.

In the figure below, we present a high–end graphics coprocessor that can be viewed as a vector processor. It is capable of a sustained rate of 4,300 Megaflops.

The NVIDIA Tesla C870

Data here are from the NVIDIA web site [R113]. I quote from their advertising copy from the year 2008. This is impressive enough; I did not bother with the figures for this year.

The C870 processor is a “massively multi–threaded processor architecture that is ideal for high performance computing (HPC) applications”.

This has 128 processor cores, each operating at 1.35 GHz. It supports the IEEE–754 single–precision standard, and operates at a sustained rate of 430 gigaflops (512 GFlops peak).

The typical power usage is 120 watts. Note the dedicated fan for cooling.

The processor has 1.5 gigabytes of DDR SDRAM, operating at 800 MHz. The data bus to memory is 384 bits (48 bytes) wide, so that the maximum sustained data rate is 76.8 Gigabytes per second.

Compare this to the CRAY–1 supercomputer of 1976, with a sustained computing rate of 136 Megaflops and a peak rate of 250 Megaflops. This is about 3.2% of the performance of the current graphics coprocessor at about 500 times the cost. The Cray Y–MP was a supercomputer sold by Cray Research beginning in 1988. Its peak performance was 2.66 Gigaflops (8 processors at 333 Megaflops each). Its memory comprised 128, 256, or 512 MB of static RAM. The earliest supercomputer that could outperform the current graphics processor seems to have been the Cray T3E–1200E™, a MPP (Massively Parallel Processor) introduced in 1995 (Ref. 9). In 1998, a joint scientific team from Oak Ridge National Lab, the University of Bristol (UK) and others ran a simulation related to controlled fusion at a sustained rate of 1.02 Teraflops (1020 Gigaflops).

Sample Problem: 2–D Matrix Multiplication

We now turn to a simple mathematics problem that illustrates the structure of a problem that is well suited to execution on the GRU part of the CUDA. We shall begin with simple sequential code and modify it in stages until it is structured for parallel execution.

Here we consider the multiplication of two square matrices, each of size N–by–N, having row and column indices in the range [0, N – 1]. The following is code such as one might see in a typical serial implementation to multiply square matrix A by square matrix B, producing square matrix C.

For I = 0 to (N – 1) Do

For J = 0 to (N – 1) Do

Sum = 0 ;

For K = 0 to (N – 1) Do

SUM = SUM + A[I][K]·B[K][J] ;

End For

C[I][J] = SUM ;

End For

Note the use of SUM to avoid multiple references to C[I][J] within the inner loop.

Memory Organization of 2–D Arrays

In order to write efficient array code of any sort one has to understand the organization of multiply dimensioned arrays in computer memory. The most efficient way to handle two dimensional arrays will be to treat them as one dimensional arrays. We are moving towards a parallel implementation in which the computation of any number of matrix functions of two square N–by–N matrices can be done very efficiently in parallel by an array of N² processors; each computing the results for one element in the result array.

Doing this efficiently means that we must reduce all arrays to one dimension, in the way that the run–time support systems for high–level languages do. Two–dimensional arrays make for good examples of this in that they represent the simplest data structures in which this effect is seen. Multiply dimensioned arrays are stored in one of two fashions: row major order and column major order. Consider a 2–by–3 array X.

In row major order, the rows are stored contiguously.
X[0][0], X[0][1], X[0][2], X[1][0], X[1][1], X[1][0]

Most high–level languages use row major ordering.

In column major order, the columns are stored contiguously
X[0][0], X[1][0], X[0][1], X[1][1], X[0][2], X[1][2]

Old FORTRAN is column major.

We shall assume that the language for implementing this problem supports row major ordering. In that case, we have two ways to reference elements in the array.

Two indices X[0][0] X[0][1] X[0][2] X[1][0] X[1][1] X[1][0]
One index X[0] X[1] X[2] X[3] X[4] X[5]

The index in the “one index” version is the true offset of the element in the array.

Sample Problem Code Rewritten

The following is code shows the one–dimensional access to the 2–dimensional
arrays A, B, C. Each has row and column indices in the range [0, N – 1].

For I = 0 to (N – 1) Do

For J = 0 to (N – 1) Do

Sum = 0 ;

For K = 0 to (N – 1) Do

SUM = SUM + A[I·N + K]·B[K·N + J] ;

End For

C[I·N + J] = SUM ;

End For

Note that the [I][J] element of an N–by–N array is at offset [I·N + J].

Some Issues of Efficiency

The first issue is rather obvious and has been assumed. We might have written the code as:

For K = 0 to (N – 1) Do

C[I·N + J] = C[I·N + J] + A[I·N + K]·B[K·N + J] ;

End For

But note that this apparently simpler construct leads to 2·N references to array element C[I·N + J] for each value of I and J. Array references are expensive, because the compiler must generate code that will allow access to any element in the array.

Our code has one reference to C[I·N + J] for each value of I and J.

Sum = 0 ;

For K = 0 to (N – 1) Do

SUM = SUM + A[I·N + K]·B[K·N + J] ;

End For

C[I·N + J] = SUM ;

Array Access: Another Efficiency Issue

In this discussion, we have evolved the key code statement as follows. We began with
SUM = SUM + A[J][L]·B[L][K] and changed to
SUM = SUM + A[I·N + K]·B[K·N + J]

The purpose of this evolution was to make explicit the mechanism by which the address of an element in a two–dimensional array is determined. This one–dimensional access code exposes a major inefficiency that is due to the necessity of multiplication to determine the addresses of each of the two array elements in this statement. Compared to addition, multiplication is a very time–consuming operation.

As written the key statement SUM = SUM + A[I·N + K]·B[K·N + J] contains three multiplications, only one of which is essential to the code. We now exchange the multiplication statements in the address computations for addition statements, which execute much more quickly.

Addition to Generate Addresses in a Loop

Change the inner loop to define and use the indices L and M as follows.

For K = 0 to (N – 1) Do

L = I·N + K ;

M = K·N + J ;

SUM = SUM + A[L]·B[M] ;

End For

For K = 0 L = I·N M = J

For K = 1 L = I·N + 1 M = J + N

For K = 2 L = I·N + 2 M = J + 2·N

For K = 3 L = I·N + 3 M = J + 3·N

The Next Evolution of the Code

This example eliminates all but one of the unnecessary multiplications.

For I = 0 to (N – 1) Do

For J = 0 to (N – 1) Do

Sum = 0 ;

L = I·N ;

M = J ;

For K = 0 to (N – 1) Do

SUM = SUM + A[L]·B[M] ;

L = L + 1 ;

M = M + N ;

End For

C[I·N + J] = SUM ;

End For

Suppose a Square Array of Processors

Suppose an array of N² processors, one for each element in the product array C. Each of these processors will be assigned a unique row and column pair. Assume that process (I, J) is running on processor (I, J) and that there is a global mechanism for communicating these indices to each process.

Sum = 0 ;

L = I·N ;

M = J ;

INJ = L + M ; // Note we have I·N + J computed here.

For K = 0 to (N – 1) Do

SUM = SUM + A[L]·B[M] ;

L = L + 1 ;

M = M + N ;

End For

C[INJ] = SUM ;

For large values of N, there is a significant speedup to be realized.

Another Look at the NVIDIA GeForce 8800 GTX

Here, your author presents a few random thoughts about this device. As noted in the textbook, a “fully loaded” device has 16 multiprocessors, each of which contains 8 streaming processors operating at 1.35 GHz. Each streaming processor has a local memory with capacity of 16 KB, along with 8,192 (2¹³) 32–bit registers.

The work load for computing is broken into threads, with a thread block being defined as a number of intercommunicating threads that must execute on the same streaming processor. A block can have up to 512 (2⁹) threads.

Conjecture: This division allows for sixteen 32–bit registers per thread.

Fact: The maximum performance of this device is 345.6 GFLOPS
(billion floating point operations per second)

On 4/17/2010, the list price was $1320 per unit, which was
discounted to $200 per unit on Amazon.com.

Fact: In 1995, the fastest vector computer was a Cray T932. Its maximum
performance was just under 60 GFLOPS. It cost $39 million.

Some Final Words on CUDA

As has been noted above in this text, the graphical processing units are designed to be part of a computational pair, along with a traditional CPU. Examination of the picture of the NVIDIA Tesla C870 shows it to be a coprocessor, to be attached to the main computer bus. It turns out that the device uses a PCI Express connection.

The best way to use a CUDA is to buy an assembled PC with the GPU attached. Fortunately these are quite reasonable. In July 2011, one could buy a Dell Precision T7500 with a Quad Core Xeon Processor (2.13 GHz), 4 GB of DDR3 RAM, a 250 GB SATA disk, and an attached NVIDIA Tesla C2050, all for about $5,000.

Clusters, Grids, and the Like

There are many applications amenable to an even looser grouping of multicomputers. These often use collections of commercially available computers, rather than just connecting a number of processors together in a special network. In the past there have been problems of administering large clusters of computers; the cost of administration scaling as a linear function of the number of processors. Recent developments in automated tools for remote management are likely to help here.

It appears that blade servers are one of the more recent adaptations of the cluster concept. The major advance represented by blade servers is the ease of mounting and interconnecting the individual computers, called “blades”, in the cluster. In this aspect, the blade server hearkens back to the 1970’s and the innovation in instrumentation called “CAMAC”, which was a rack with a standard bus structure for interconnecting instruments. This replaced the jungle of interconnecting wires, so complex that it often took a technician dedicated to keeping the communications intact.

Clusters can be placed in physical proximity, as in the case of blade servers, or at some distance and communicate via established networks, such as the Internet. When a network is used for communication, it is often designed using TCP/IP on top of Ethernet simply due to the wealth of experience with this combination.

A Few Examples of Clusters, Grids, and the Like

In order to show the variety of large computing systems, your author has selected a random collection. Each will be described in a bit of detail.

The E25K NUMA Multiprocessor by Sun Microsystems

Our first example is a shared–memory NUMA multiprocessor built from seventy–two processors. Each processor is an UltraSPARC IV, which itself is a pair of UltraSPARC III Cu processors. The “Cu” in the name refers to the use of copper, rather than aluminum, in the signal traces on the chip. A trace can be considered as a “wire” deposited on the surface of a chip; it carries a signal from one component to another. Though more difficult to fabricate than aluminum traces, copper traces yield a measurable improvement in signal transmission speed, and are becoming favored.

Recall that NUMA stands for “Non–Uniform Memory Access” and describes those multiprocessors in which the time to access memory may depend on the module in which the addressed element is located; access to local memory is much faster than access to memory on a remote node. The basic board in the multiprocessor comprises the following:

1. A CPU and memory board with four UltraSPARC IV processors, each with an 8–GB
memory. As each processor is dual core, the board has 8 processors and 32 GB memory.

2. A snooping bus between the four processors, providing for cache coherency.

3. An I/O board with four PCI slots.

4. An expander board to connect all of these components and provide communication
to the other boards in the multiprocessor.

A full E25K configuration has 18 boards; thus 144 CPU’s and 576 GB of memory.

The E25K Physical Configuration

Here is a figure from Tanenbaum [R15] depicting the E25K configuration.

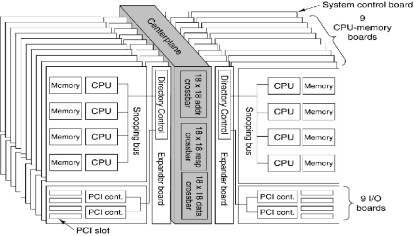
The E25K has a centerplane with three 18–by–18 crossbar switches to connect the boards. There is a crossbar for the address lines, one for the responses, and one for data transfer.

The number 18 was chosen because a system with 18 boards was the largest that would fit through a standard doorway without being disassembled. Design constraints come from everywhere.

Cache Coherence in the E25K

How does one connect 144 processors (72 dual–core processors) to a distributed memory and still maintain cache coherence? There are two obvious solutions: one is too slow and the other is too expensive. Sun Microsystems opted for a multilevel approach, with cache snooping on each board and a directory structure at a higher level. The next figure shows the design.

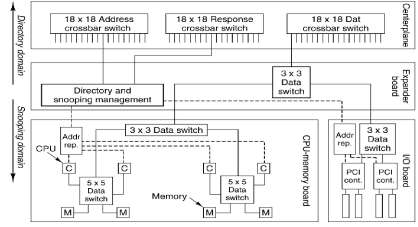
The memory address space is broken into blocks of 64 bytes each. Each block is assigned a “home board”, but may be requested by a processor on another board. Efficient algorithm design will call for most memory references to be served from the processors home board.

The IBM BlueGene

The description of this MPP system is based mostly on Tanenbaum [R15]. The system was designed in 1999 as “a massively parallel supercomputer for solving computationally–intensive problems in, among other fields, the life sciences”. It has long been known that the biological activity of any number of important proteins depends on the three dimensional structure of the protein. An ability to model this three dimensional configuration would allow the development of a number of powerful new drugs.

The BlueGene/L was the first model built; it was shipped to Lawrence Livermore Lab in June 2003. A quarter–scale model, with 16,384 processors, became operational in November 2004 and achieved a computational speed of 71 teraflops. The full model, with 65,536 processors, was scheduled for delivery in the summer of 2005. In October 2005, the full system achieved a peak speed on 280.6 teraflops on a standard benchmark called “Linpack”. On real problems, it achieved a sustained speed of over 100 teraflops.

The Custom Processor Chip

IBM intended the BlueGene line for general commercial and research applications. Because of this, the company elected to produce the processor chips from available commercial cores. Each processor chip has two PowerPC 440 cores operating at 700 MHz. The configuration of the chip, with its multiple caches is shown in the figure below. Note that only one of the two cores is dedicated to computation, the other is dedicated to handling communications.

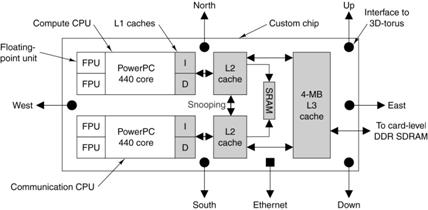
Description: 8-36

The connection topology used in the BlueGene is a three–dimensional torus. Each processor chip is connected to six other processor chips. The connections are called “North”, “East”, “South”, “West”, “Up”, and “Down”. Think of a three–dimensional cube with 6 faces.

In a recent upgrade (June 2007), IBM upgraded this chip to hold four PowerPC 450 cores operating at 850 MHz. In November 2007, the new computer, called the BlueGene/P achieved a sustained performance of 167 teraflops. This design obviously has some “growing room”.

The BlueGene/L Hierarchy

The 65,536 BlueGene/L is designed in a hierarchical fashion. There are two chips per card,
16 cards per board, 32 boards per cabinet, and 64 cabinets in the system.

We shall see that the MPP systems manufactured by Cray, Inc. follow the same design philosophy. It seems that this organization will become common for large MPP systems.

The AMD Opteron

Before continuing with our discussion of MPP systems, let us stop and examine the chip that has recently become the favorite for use as the processor, of which there are thousands. This chip is the AMD Opteron, which is a 64–bit processor that can operate in three modes.

In legacy mode, the Opteron runs standard Pentium binary programs unmodified.

In compatibility mode, the operating system runs in full 64–bit mode, but applications
must run in 32–bit mode.

In 64–bit mode, all programs can issue 64–bit addresses; both 32–bit and 64–bit
programs can run simultaneously in this mode.

The Opteron has an integrated memory controller, which runs at the speed of the processor clock. This improves memory performance. It can manage 32 GB of memory. The Opteron comes in single–core, dual–core, or quad–core processors. The standard clock rates for these processors range from 1.7 to 2.3 GHz.

The Red Storm by Cray, Inc.

The Red Storm is a MPP system in operation at Sandia National Laboratory. This lab, operated by Lockheed Martin, doe classified work for the U.S. Department of Energy. Much of this work supports the design of nuclear weapons. The simulation of nuclear weapon detonations, which is very computationally intensive, has replaced actual testing as a way to verify designs.

In 2002, Sandia selected Cray, Inc. to build a replacement for its current MPP, called ASCI Red. This system had 1.2 terabytes of RAM and operated at a peak rate of 3 teraflops. The Red Storm was delivered in August 2004 and upgraded in 2006 [Ref. 9]. The Red Storm now uses dual–core AMD Opterons, operating at 2.4 GHz. Each Opteron has 4 GB of RAM and a dedicated custom network processor called the Seastar, manufactured by IBM. Almost all data traffic between processors moves through the Seastar network, so great care was taken in its design. This is the only chip that is custom–made for the project.

The next step in the architecture hierarchy is the board, which holds four complete Opteron systems (four CPU’s, 16 GB RAM, four Seastar units), a 100 megabit per second Ethernet chip, and a RAS (Reliability, Availability, and Service) processor to facilitate fault location. The next step in the hierarchy is the card cage, which comprises eight boards inserted into a backplane. Three card cages and their supporting power units are placed into a cabinet. The full Red Storm system comprises 108 cabinets, for a total of 10,836 Opterons and 10 terabytes of SDRAM. Its theoretical peak performance is 124 teraflops, with a sustained rate of 101 teraflops (10¹² floating–point operations per second).

Security Implications of the Architecture

In the world on national laboratories there are special requirements on the architecture of computers that might be used to process classified data. The Red Storm at Sandia routinely processes data from which the detailed design of current U.S. nuclear warheads may be inferred. Naturally, such data are considered to be quite sensitive. The solution to the security problem was to partition Red Storm into classified and unclassified sections. This partitioning was done by mechanical switches, which would completely isolate one section from another. There are three sections: classified, unclassified, and a switchable section.

Description: 8-39

The Cray XT5h

The Cray XT3 is a commercial design based on the Red Storm installed at Sandia National Labs. The Cray XT3 led to the development of the Cray XT4 and Cray XT5, the latest in the line. The XT5 follows the Red Storm approach in using a large number of AMD Opteron processors. The processor interconnect uses the same three–dimensional torus as found in the IBM BlueGene and presumably in the Cray Red Storm. The network processor has been upgraded to a system called ‘Seastar 2+”; each switch having six 9.6 GB/second router–to–router ports.

The Cray XT5h is a modified XT5, adding vector coprocessors and FPGA (Field Programmable Gate Array) accelerators. FPGA processors might be used to handle specific calculations, such as Fast Fourier Transforms, which often run faster on these units than on general purpose processors. We may expect to see a number of heterogeneous processors.

In April 2008, Cray, Inc. was chosen to deliver an XT4 to the University of Tennessee. This monster was advertised to achieve one petaflop (1000 teraflops) in performance. When installed, the computer was called “The Jaguar”. Here is a picture from the web site of the U.S. National Center for Computational Sciences [R115].

As of July 2011, the computer showed a peak seed of 2.33 petaflops (2.33·10¹⁵ floating point operations per second), and a sustained performance in excess of 1.0 petaflop. The upgraded system has an 84–cabinet Cray XT4 and a200–cabinet upgraded Cray XT5. Each XT4 has 8 gigabytes per node, and each XT5 has 16 gigabytes per node, for a total of 362 terabytes of high speed memory. The total processor count is 37,376 six–core AMD Opterons (in the XT5) and 7,832 quad–core AMD Opterons (in the XT4). The XT4 part of the system is air cooled, but the XT5 part must be liquid cooled, using the commercial refrigerant R–134. The Jaguar requires 12.7 megawatts of electric power and a continuous supply of chilled air and refrigerant.

In every sense of the word, this is a big computer.