The Underlying Technologies
A standard presentation of the history of computing machines (now called computers) begins with a list of the generations of computers based on the technologies used to fabricate the CPU (Central Processing Unit) of the computer. These base technologies can be listed in four categories, corresponding somewhat to the generations that are to be defined later. These technologies are: 1) Mechanical components, including electromechanical relays, 2) Vacuum tubes,
3) Discrete transistors, and
4) Integrated circuits, divided into several
important classes.
To a lesser extent, we need to look at technologies used to fabricate computer memories, including magnetic cores and semiconductor memories.
Mechanical Components
All early computational devices, from the abacus to adding machines of the 1950’s and early 1960’s were hand-operated, with components that were entirely mechanical. These were made entirely of wood and/or metal and were quite slow in comparison to any modern electronic devices. The limitation of speed of such devices was due to the requirement to move a mass of material; thus incurring the necessity to overcome inertia. Those students who want to investigate inertia are requested either to study physics or to attempt simple experiments involving quick turns when running quickly (but not with scissors).
Analog and Digital Computers
With one very notable exception, most mechanical computers would be
classified as analog devices. In
addition to being much slower than modern electronic devices, these computers
suffered from poor accuracy due to slippages in gears and pulleys. We support this observation with a brief
definition and definition of the terms “analog” and “digital”.
Within the context of this discussion, we use the term “digital” to mean that the values are taken from a discrete set that is not continuous. Consider a clinical thermometer used to determine whether or not a small child has a fever. If it is an old-fashioned mercury thermometer, it is an analog device in that the position of the mercury column varies continuously. Another example would be the speedometer on most modern automobiles, it is a dial arrangement, where the indicator points to a number and moves continuously.
The author of these notes knows of one mechanical computer that can be considered to be digital. This is the abacus. As the student probably knows, the device records numbers by the position of beads on thin rods. While the beads are moved continuously, in general each bead must be in one of two positions in order for the abacus to be in a correct state.
Figure: Abacus Bead Moves From One
Position to The Other
Modern binary digital computers follow a similar strategy of having only two correct “positions”, thereby gaining accuracy. Such computers are based on electronic voltages, usually in the range 0.0 to 5.0 volts or 0.0 to 2.5 volts. Each circuit in the design has a rule for correcting slight imperfections in the voltage levels. In the first scheme, called TTL after the name of its technology (defined later), a voltage in the range 0.0 to 0.8 volts is corrected to 0.0 volts and a voltage in the range 2.8 to 5.0 volts is corrected to 5.0 volts. The TTL design reasonably assumes that voltages in the range 0.8 to 2.8 volts do not occur; should such a voltage actually occur, the behavior of the circuit will be unpredictable.
We have departed from our topic of mechanical computers, but we have a good discussion going so we shall continue it. In an analog electronic computer, a voltage of 3.0 would have a meaning different than a voltage of 3.1 or 2.9. Suppose that our intended voltage were 3.0 and that a noise signal of 0.1 volts has been added to the circuit. The level is now 3.1 volts and the meaning of the stored signal has changed; this is the analog accuracy problem. In the digital TTL world, such a signal would be corrected to 5.0 volts and hence its correct value.
A
speedometer in an average car presents an excellent example of a mechanical
analog computer, although it undoubtedly uses some electromagnetic
components. The device has two displays
of importance – the car speed and total distance driven. Suppose we start the automobile at time T = 0
and make the following definitions.
S(T) the speed of the car at time T, and
X(T) the distance the car has been driven up to time T.
As noted later, mechanical computers were often used to produce numerical solutions to differential and integral equations. Our automobile odometer provides a solution to either of the two equivalent equations.
![]() = S(T)
= S(T)
X(T) = 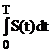
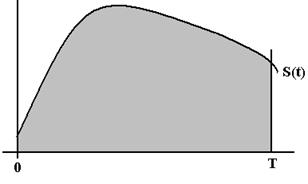
Figure: The Integral is the Area Under
the Curve
The problem with such a mechanical computer is that slippage in the mechanism can cause inaccuracies. The speedometer on this author’s car is usually off by about 1.5%. This is OK for monitoring speeds in the range 55 to 70 mph, but not sufficient for scientific calculations.
Electronic Relays
Electronic relays are devices that use (often small) voltages to switch larger voltages. One example of such a power relay is the horn relay found in all modern automobiles. A small voltage line connects the horn switch on the steering wheel to the relay under the hood. It is that relay that activates the horn.
The following figure illustrates the operation of an electromechanical relay. The iron core acts as an electromagnet. When the core is activated, the pivoted iron armature is drawn towards the magnet, raising the lower contact in the relay until it touches the upper contact, thereby completing a circuit. Thus electromechanical relays are switches.
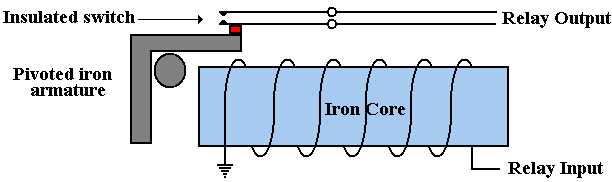
Figure: An Electromechanical Relay
In general, an electromechanical relay is a device that uses an electronic voltage to activate an electromagnet that will pull an electronic switch from one position to another, thus affecting the flow of another voltage; thereby turning the device “off” or “on”. Relays display the essential characteristic of a binary device – two distinct states. Below we see pictures of two recent-vintage electromechanical relays.

Figure: Two Relays (Source
http://en.wikipedia.org/wiki/Relay)
The primary difference between the two types of relays shown above is the amount of power being switched. The relays for use in general electronics tend to be smaller and encased in plastic housing for protection from the environment, as they do not have to dissipate a large amount of heat. Again, think of an electromechanical relay as an electronically operated switch, with two possible states: ON or OFF.
Power relays, such as the horn relay, function mainly to isolate the high currents associated with the switched apparatus from the device or human initiating the action. One common use is seen in electronic process control, in which the relays isolate the electronics that compute the action from the voltage swings found in the large machines being controlled.
In use for computers, relays are just switches that can be operated electronically. To understand their operation, the student should consider the following simple circuits.
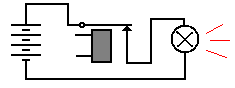
Figure: Relay Is Closed: Light Is
Illuminated
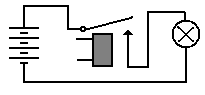
Figure: Relay Is Opened: Light Is Dark.
We may use these simple components to generate the basic Boolean functions, and from these the more complex functions used in a digital computer. The following relay circuit implements the Boolean AND function, which is TRUE if and only if both inputs are TRUE. Here, the light is illuminated if and only if both relays are closed.
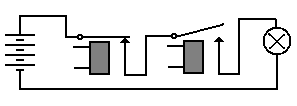
Figure: One Closed and One Open
Computers based on electromagnetic relays played an important part in the early development of computers, but became quickly obsolete when designs using vacuum tubes (considered as purely electronic relays) were introduced in the late 1940’s. These electronic tubes also had two states, but could be switched more quickly as there were no mechanical components to be moved.
Vacuum Tubes
The next figure shows a
picture of an early vacuum tube, along with its schematic and a circuit showing
a typical use. The picture and
schematics are taken from the web page of Dr. Elizabeth R. Tuttle of the
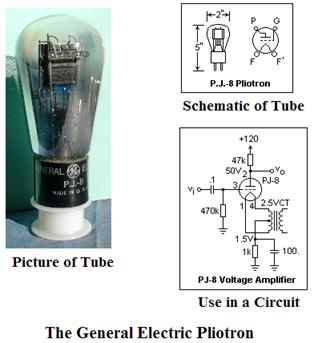
This particular vacuum tube seems to have been manufactured in the 1920’s. Later vacuum tubes (such as from the 1940’s and 1950’s) tended to me much smaller.
The vacuum tube shown above is a triode, which is a device with three major components, a cathode, a grid, and an anode. The cathode is the element that is the source of electrons in the tube. When it is heated either directly (as a filament in a light bulb) or indirectly by a separate filament, it will emit electrons, which either are reabsorbed by the cathode or travel to the anode. When the anode is held at a voltage more positive than the cathode, the electrons tend to flow from cathode to anode (and the current is said to flow from anode to cathode – a definition made in the early 19th century before electrons were understood). The third element in the device is a grid, which serves as an adjustable barrier to the electrons. When the grid is more positive, more electrons tend to leave the cathode and fly to the anode. When the grid is more negative, the electrons tend to stay at the cathode. By this mechanism, a small voltage change applied to the grid can cause a larger voltage change in the output of the triode; hence it is an amplifier. As a digital device, the grid in the tube either allows a large current flow or almost completely blocks it – “on” or “off”.
Here we should add a note related to analog audio devices, such as high–fidelity and stereo radios and record players. Note the reference to a small voltage change in the input of a tube causing a larger voltage change in the output; this is amplification, and tubes were once used in amplifiers for audio devices. The use of tubes as digital devices is just a special case, making use of the extremes of the range and avoiding the “linear range” of amplification.
We close this section with a picture taken from the IBM 701 computer, a computer from 1953 developed by the IBM Poughkeepsie Laboratory. This was the first IBM computer that relied on vacuum tubes as the basic technology.

Figure: A Block of Tubes from the IBM 701
Source: [R23]
The reader will note that, though there is no scale on this drawing, the tubes appear smaller than the Pliotron, and are probably about one inch in height. The components that resemble small cylinders are resistors; those that resemble pancakes are capacitors.
Another feature of the figure above that is worth note is the fact that the vacuum tubes are grouped together in a single component. The use of such components probably simplified maintenance of the computer; just pull the component, replace it with a functioning copy, and repair the original at leisure.
There are two major difficulties with computers fabricated from vacuum tubes, each of which arises from the difficulty of working with so many vacuum tubes. Suppose a computer that uses 20,000 vacuum tubes; this being only slightly larger than the actual ENIAC.
A vacuum tube requires a hot filament in order to function. In this it is similar to a modern light bulb that emits light due to a heated filament. Suppose that each of our tubes requires only five watts of electricity to keep its filament hot and the tube functioning. The total power requirement for the computer is then 100,000 watts or 100 kilowatts.
We also realize the problem of reliability of such a large collection of tubes. Suppose that each of the tubes has a probability of 99.999% of operating one hour. This can be written as a decimal number as 0.99999 = 1.0 – 10-5. The probability that all 20,000 tubes will be operational for more than an hour can be computed as (1.0 – 10-5)20000, which can be approximated as 1.0 – 20000·10-5 = 1.0 – 0.2 = 0.8. There is an 80% chance the computer will function for one hour and 64% chance for two hours of operation. This is not good.
Discrete Transistors
Discrete transistors can be thought of as small triodes with the additional advantages of consuming less power and being less likely to wear out. The reader should note the transistor second from the left in the figure below. It at about one centimeter in size would have been an early replacement for the vacuum tube of about 5 inches (13 centimeters) in size shown on the previous page. One reason for the reduced power consumption is that there is no need for a heated filament to cause the emission of electrons.

When first introduced, transistors immediately presented an enormous (or should we say small – think size issues) advantage over the vacuum tube. However, there were cost disadvantages, as is noted in this history of the TX-0, a test computer designed around 1951.
The TX-0 had 18-bit words and 3,600 transistors.
“Like the MTC [Memory Test Computer], the TX-0 was designed as a test device. It was designed to test transistor circuitry, to verify that a 256 X 256 (64–K word) core memory could be built … and to serve as a prelude to the construction of a large-scale 36-bit computer. The transistor circuitry being tested featured the new Philco SBT100 surface barrier transistor, costing $80, which greatly simplified transistor circuit design.” [R01, page 127]
That is a cost of $288,000 just for the transistors. Imagine the cost of a 256 MB memory, since each byte of memory would require at least eight, and probably 16, transistors.
The figure below shows some
of the symbols used to denote transistors in circuit diagrams.
For this course, it is not necessary to interpret these diagrams.
Integrated Circuits
Integrated circuits are nothing more or less than a very efficient packaging of transistors and other circuit elements. The term “discrete transistors” implied that the circuit was built from transistors connected by wires, all of which could be easily seen and handled by humans.
Integrated circuits were
introduced in response to a problem that occurred in designs that used discrete
transistors. With the availability of
small and effective transistors, engineers of the 1950’s looked to build
circuits of greater complexity and functionality. They discovered a number of problems inherent
in the use of transistors.
1) The
complexity of the wiring schemes.
Interconnecting the transistors became the
major stumbling block to the
development of large useful circuits.
2) The
time delays associated with the longer wires between the discrete transistors.
A faster circuit must have
shorter time delays.
3) The
actual cost of wiring the circuits, either by hand or by computer aided design.
It was soon realized that assembly
of a large computer from discrete components would be almost impossible, as
fabricating such a large assembly of components without a single faulty
connection or component would be extremely costly. This problem became known as the “tyranny of
numbers”. Two teams independently sought
solutions to this problem. One team at
Texas Instruments was headed by Jack Kilby, an engineer with a background in
ceramic-based silk screen circuit boards and transistor-based hearing
aids. The other team was headed by
research engineer Robert Noyce, a co-founder of Fairchild Semiconductor
Corporation. In 1959, each team applied
for a patent on essentially the same circuitry, Texas Instruments receiving
The first integrated circuits were classified as SSI (Small-Scale Integration) in that they contained only a few tens of transistors. The first commercial uses of these circuits were in the Minuteman missile project and the Apollo program. It is generally conceded that the Apollo program motivated the technology, while the Minuteman program forced it into mass production, reducing the costs from about $1,000 per circuit in 1960 to $25 per circuit in 1963. Were such components fabricated today, they would cost less than a penny.
It is worth note that Jack Kilby was awarded the Nobel Prize in Physics for the year 2000 as a result of his contributions to the development of the integrated circuit. While his work was certainly key in the development of the modern desk-top computer, it was only one of a chain of events that lead to this development. Another key part was the development by a number of companies of photographic-based methods for production of large integrated circuits. Today, integrated circuits are produced by photo-lithography from master designs developed and printed using computer-assisted design tools of a complexity that could scarcely have been imagined in 1960.
Integrated circuits are classified into either four or five standard groups, according to the number of electronic components per chip. Here is one standard definition.
SSI Small-scale
integration Up to 100
electronic components per chip
Introduced
in 1960.
MSI Medium-scale
integration From 100 to 3,000
electronic components per chip
Introduced
in the late 1960’s.
LSI Large-scale
integration From 3,000 to
100,000 electronic
electronic
components per chip.
Introduced
about 1970.
VLSI Very-large-scale
integration From 100,000 to 1,000,000
electronic
components
per chip
Introduced
in the 1980’s.
ULSI Ultra-large-scale
integration More than 1,000,000
electronic components
per
chip. This term is not standard and
seems
recently
to have fallen out of use.
The figure below shows some typical integrated circuits. Actually, at least two of these figures show a Pentium microprocessor, which is a complete CPU of a computer that has been realized as an integrated circuit on a single chip. The reader will note that most of the chip area is devoted to the pins that are used to connect the chip to other circuitry.

Figure: Some Late-Generation Integrated
Circuits
Note that the chip on the left has 24 pins used to connect it to other circuitry, and that the pins are arranged around the perimeter of the circuit. This chip is in the design of a DIP (Dual Inline Pin) chip. The Pentium (™ of Intel Corporation) chip has far too many pins to be arranged around its periphery, so that they are arranged along the surface of one side.
Having now described the technologies that form the basis of our descriptions of the generations of computer evolution, we now proceed to a somewhat historic account of these generations, beginning with the “generation 0” that until recently was not recognized.
The Human Computer
The history of the computer can be said to reach back in history to the first human who used his or her ability with numbers to calculate a number. While the history of computing machines must be almost as ancient as that of computers, it is not the same. The reason is that the definition of the word “computer” has changed over time. Before entering into a discussion of computing machines, we mention the fact that the word “computer” used to refer to a human being. To support this assertion, we offer a few examples.
Here are two definitions from the first edition of the Oxford English Dictionary [R10, Volume II]. The reader should note that the definitions shown for each word are the only definitions shown in the 1933 dictionary.
“Calculator – One who calculates; a reckoner”.
“Computer – One who computes; a calculator, reckoner; specifically a person employed to make calculations in an observatory, in surveying, etc.”
This last usage of the word
“computer” is seen in a history of the Royal Greenwich Observatory in
We begin our discussion of human computers with a trio from
the 18th century, three French aristocrats ( Alexis-Claude Clairaut,
Joseph-Jerome de Lalande, and Nicole-Reine Étable de la Brière
Lepaute ) who produced numerical solutions to a set of differential equations and
computed the day of return of a comet predicted by the astronomer Halley to
return in 1758. At the time,

Figure: Alexis-Claude Clairaut, Joseph-Jerome
de Lalande,
and Nicole-Reine Étable
de la Brière Lepaute
By the end of the 19th century, the work of being a computer became recognized as an accepted professional line of work. This was undertaken usually be young men and boys with not too much mathematical training, else they would not follow instructions. Most of the men doing the computational work quickly became bored and sloppy in their work. For this reason, and because they would work more cheaply, women soon formed the majority of computers. The next figure is a picture of the “Harvard Computers” in 1913. The man in the picture is the director of the Harvard College Observatory.

Figure: The Computers at the
We continue our discussion of human computers by noting three women, two of whom worked as computers during the Second World War. Many of the humans functioning as computers and calculators during this time were women for the simple reason that many of the able-bodied men were in the military.
The first computer we shall
note is Dr. Gertrude Blanch (1897–1996),
whose biography is published on the web [R18].
She received a B.S. in mathematics with a minor in physics from
We note here that mathematical tables were quite commonly used to
determine the values of most functions until the introduction of hand–held
multi–function calculators in the 1990’s.
At this point, the reader is invited to note that the name of the group
was not “Association for Computers” (which might have been an association for
the humans) but “Association for Computing Machinery”, reflecting the
still-current usage of the word “computer”.
The next person we shall note is
a woman who became involved with the ENIAC project at the Moore School of
Engineering at the
“We did have desk calculators at that time, mechanical and driven with electric motors that could do simple arithmetic. You’d do a multiplication and when the answer appeared, you had to write it down to reenter it into the machine to do the next calculation. We were preparing a firing table for each gun, with maybe 1,800 simple trajectories. To hand-compute just one of these trajectories took 30 or 40 hours of sitting at a desk with paper and a calculator. As you can imagine, they were soon running out of young women to do the calculations.” [R19]
Dr. Alan Grier of the George Washington University has studied the transition from human to electronic computers, publishing his work in a paper “Human Computers and their Electronic Counterparts” [R20], David Alan Grier from George Washington University analyzed the transition from human to electronic computers. In this paper, Dr. Grier notes that very few historians of computing bother with studying the work done before 1940, or as he put it.
“In studying either the practice or the history of computing, few individuals venture into the landscape that existed before the pioneering machines of the 1940s. …. Arguably, there is good reason for making a clean break with the prior era, as these computing machines seem to have little in common with scientific computation as it was practiced prior to 1940. At that time, the term ‘computer’ referred to a job title, not to a machine. Large-scale computations were handled by offices of human computers.”
In this paper, Dr. Grier further notes that very few of the women hired as human computers elected to make the transition to becoming computer programmers, as we currently use the term. In fact, the only women who did make the transition were the dozen or so who had worked on the ENIAC and were thus used to large scale computing machines. According to Dr. Grier [R20].
“Most human computers worked only with an adding machine or a logarithm table or a slide rule. During the 1940s and 1950s, when electronic computers were becoming more common in scientific establishments, human computers tended to view themselves as more closely to the scientists for whom they worked, rather than the engineers who were building the new machines and hence [they] did not learn programming [as the engineers did].”
Classification of Computing Machines by Generations
Before giving this classification, the author believes that he should cite directly a few web references that seem to present excellent coverage of the history of computers.
1) http://en.wikipedia.org/wiki/History_of_computing_hardware
2) http://nobelprize.org/physics/educational/integrated_circuit/history/
3) http://ei.cs.vt.edu/~history/index.html
4) http://www.yorku.ca/sasit/sts/sts3700b/syllabus.html
We take the standard classification by generations from the book Computer Structures: Principles and Examples [R04], an early book on computer architecture.
1. The first generation
(1945 – 1958) is that of vacuum tubes.
2. The
second generation (1958 – 1966) is that of discrete transistors.
3. The
third generation (1966 – 1972) is that of small-scale and medium-scale
integrated circuits.
4. The
fourth generation (1972 – 1978) is that of large-scale integrated circuits..
5. The
fifth generation (1978 onward) is that of very-large-scale integrated circuits.
This classification scheme is well established and quite useful, but does have its drawbacks. Two that are worth mention are the following.
1. It ignores the
introduction of the magnetic core memory.
The first large-scale
computer to use such memory
was the MIT Whirlwind, completed in 1952.
With
this in mind, one might
divide the first generation into two sub-generations: before
and after 1952, with those
before 1952 using very unreliable memory technologies.
2. The term “fifth
generation” has yet to be defined in a uniformly accepted way.
For many, we continue to live
with fourth-generation computers and are even now
looking forward to the next great
development that will usher in the fifth generation.
The major problem with the above scheme is that it ignores all work before 1945. To quote an early architecture book, much is ignored by this ‘first generation’ label.
“It is a measure of American industry’s generally ahistorical view of things that the title of ‘first generation’ has been allowed to be attached to a collection of machines that were some generations removed from the beginning by any reasonable accounting. Mechanical and electromechanical computers existed prior to electronic ones. Furthermore, they were the functional equivalents of electronic computers and were realized to be such.” [R04, page 35]
Having noted the criticism, we follow other authors in surveying “generation 0”, that large collection of computing devices that appeared before the official first generation.
Mechanical Ancestors
(Early generation 0)
The earliest computing
device was the abacus; it is interesting to note that it is still in use. The earliest form of abacus dates to 450 BC
in the western world and somewhat earlier in
For those who like visual examples, we include a picture of a modern abacus.

Figure: A Modern Abacus
In 1617, John Napier of
Merchiston (Scotland) took the next step in the development of mechanical
calculators when he published a description of his numbering rods, since known
as ‘Napier’s bones’ for facilitating the multiplication of numbers. The set that belonged to Charles Babbage is
preserved in the
The first real calculating
machine, as the term is generally defined, was invented by the French
philosopher Blaise Pascal in 1642. It
was improved in 1671 by the German scientist Gottfried Wilhelm Leibniz, who
developed the idea of a calculating machine which would perform multiplication
by rapidly repeated addition. It was not
until 1694 that his first complete machine was actually constructed. This machine is still preserved in the Royal
Library at
A Diversion to Discuss Weaving – the Jacquard Loom
It might seem strange to divert from a discussion of computing machinery to a discussion of machinery for weaving cloth, but we shall soon see a connection. Again, the invention of the Jacquard loom was in response to a specific problem. In the 18th century, manual weaving from patterns was quite common, but time-consuming and plagued with errors. By 1750 it had become common to use punched cards to specify the pattern. At first, these instructions punched on cards were simply interpreted by the person (most likely a boy, as child labor was common in those days). Later modifications included provisions for mechanical reading of the pattern cards by the loom. The last step in this process was taken by Joseph Jacquard in 1801 when he produced a successful loom in which all power was supplied mechanically and control supplied by mechanical reading of the punched cards; thus becoming one of the first programmable machines controlled by punched cards.

We divert from this
diversion to comment on the first recorded incident of industrial
sabotage. One legend concerning Jacquard
states that during a public exhibition of his loom, a group of silk workers
cast shoes, called “sabots”, into the mechanism in an attempt to destroy
it. What is known is that the word “sabotage”
acquired a new meaning, with this meaning having become common by 1831, when
the silk workers revolted. Prior to about
1830, the most common meaning of the word “sabotage” was “to use the wooden
shoes
[sabots] to make loud noises”.
Charles Babbage and His Mechanical Computers
Charles Babbage (1792 – 1871) designed two computing machines, the difference engine and the analytical engine. The analytical engine is considered by many to be the first general-purpose computer. Unfortunately, it was not constructed in Babbage’s lifetime, possibly because the device made unreasonable demands on the milling machines of the time and possibly because Babbage irritated his backers and lost financial support.
Babbage’s first project, called the difference engine, was begun in 1823 as a solution to the problem of computing navigational tables. At the time, most computation was done by a large group of clerks (preferably not mathematically trained, as the more ignorant clerks were more likely to follow directions) who worked under the direction of a mathematician. Errors were common both in the generation of data for these tables and in the transcription of those data onto the steel plates used to engrave the final product.
The difference engine was designed to calculate the entries of a table automatically, using the mathematical technique of finite differences (hence the name) and transfer them via steel punches directly to an engraver’s plate, thus avoiding the copying errors. The project was begun in 1823, but abandoned before completion almost 20 years later. The British government abandoned the project after having spent £17,000 (about $1,800,000 in current money – see the historical currency converter [R24]) on it and concluding that its only use was to calculate the money spent on it.
The above historical comment should serve as a warning to those of us who program computers. We are “cost centers”, spending the money that other people, the “profit centers”, generate. We must keep these people happy or risk losing a job.

Figure: Modern Recreation of Babbage’s
Analytical Engine

Figure: Scheutz’s Differential Engine
(1853) – A Copy of Babbage’s Machine
The reader will note that each of Babbage’s machine and Scheutz’s machine are hand cranked. In this they are more primitive than Jacquard’s loom, which was steam powered.
Babbage’s analytical engine was designed as a general-purpose computer. The design, as described in an 1842 report (http://www.fourmilab.ch/babbage/sketch.html) by L. F. Menebrea, calls for a five-component machine comprising the following.
1) The Store A memory fabricated from a set of counter wheels.
This
was to hold 1,000 50-digit numbers.
2) The Mill Today,
we would call this the Arithmetic-Logic Unit
3) Operation Cards Selected one of four operations: addition, subtraction,
multiplication,
or division.
4) Variable Cards Selected the memory location to be used by the operation.
5) Output Either
a printer or a punch.
This design represented a
significant advance in the state of the art in automatic computing for a number
of reasons.
1) The
device was general-purpose and programmable,
2) The
provision for automatic sequence control,
3) The
provision for testing the sign of a result and using that information
in the sequencing decisions,
and
4) The
provision for continuous execution of any desired instruction.
To complete our discussion of Babbage’s analytical engine, we include a program written to solve two simultaneous linear equations.
m·x + n·y = d
m’·x + n’·y = d’
As noted in the report by Menebrea, we have x = (d·n’ – d·’n) / (m·n’ – m’·n). The program to solve this problem, shown below, seems to be in assembly language.

Source: See R25
No discussion of Babbage’s
analytical engine would be complete without a discussion of Ada Byron, Lady
Lovelace. We have a great description
from a web article written by Dr. Betty Toole [R26]. Augusta Ada Byron was born on December 10,
1815, the daughter of the famous poet Lord Byron. Five weeks after
When she was 17,
Babbage continued to work on
plans for his analytical engine. In
1841, Babbage reported on progress at a seminar in
Bush’s Differential Analyzer
Some of the problems associated with early mechanical computers are illustrated by this picture of the Bush Differential Analyzer, built by Vannevar Bush of MIT in 1931. It was quite large and all mechanical, very heavy, and had poor accuracy (about 1%). [R21]

Figure: The Bush Differential Analyzer
For an idea of scale in this picture, the reader should note that the mechanism is placed on a number of tables (or lab benches), each of which would be waist high.
For the most part, computers with mechanical components were analog devices, set up to solve integral and differential equations. These were based on an elementary device, called a planimeter that could be used to produce the area under a curve. The big drawback to such a device was that it relied purely on friction to produce its results; the inevitable slippage being responsible for the limited accuracy of the machines.
A machine such as Bush’s differential analyzer had actually been proposed by Lord Kelvin in the nineteenth century, but it was not until the 1930’s that machining techniques were up to producing parts with the tolerances required to produce the necessary accuracy.
The differential analyzer was originally designed in order to solve differential equations associated with power networks but, as was the case with other computers, it was pressed into service for calculation of trajectories of artillery shells. There were five different copies of the differential analyzer produced; one was used at the Moore School of Engineering where it must have been contemporaneous with the ENIAC. The advent of electronic digital computers quickly made the mechanical analog computers obsolete, and all were broken up and mostly sold for scrap in the 1950’s. Only a few parts have been saved from the scrap heap and are now preserved in museums. There is no longer a fully working mechanical differential analyzer from that period.
To finish this section on mechanical calculators, we show a picture of a four-function mechanical calculator produced by the Monroe Corporation about 1953. Note the hand cranks and a key used to reposition the upper part, called the “carriage”.

Figure: A
The purely mechanical calculators survived the introduction of the electronic computer by a number of years, mostly due to economic issues – the mechanicals were much cheaper, and they did the job.
Electromechanical
Ancestors (Late generation 0 – mid 1930’s to 1952)
The next step in the development of automatic computers occurred in 1937, when George Stibitz, a mathematician working for Bell Telephone Laboratories designed a binary full adder based on electromechanical relays. Dr. Stibitz’s first design, developed in November 1937, was called the “Model K” as it was developed in his kitchen at home.
In late 1938, Bell Labs launched a research project with Dr. Stibitz as its director. The first computer was the Complex Number Calculator, completed in January 1940. This computer was designed to produce numerical solutions to the equations (involving complex numbers) that arose in the analysis of transmission circuits.
Stibitz worked in conjunction with a Bell Labs team, headed by Samuel Williams, to develop first a machine that could calculate all four basic arithmetic functions, and later to develop the Bell Labs Model Relay Computer, now recognized as the worlds first electronic digital computer. [R27]
|
. |
Model 11 |
Model III |
Model IV |
Model V |
|
Date completed |
7-1943 |
6-1944 |
3-1945 |
12-1946, 8-1947 |
|
Date dismantled |
1961 |
1958 |
1961 |
1958 |
|
Place installed |
|
|
|
|
|
Also known as |
Relay |
Ballistic |
Error Detector |
|
|
No. relays |
440 |
1,400 |
1,425 |
9,000+ |
|
Word length |
2 to 5 |
1 to 6 |
1 to 6 |
1 to 7 |
|
Memory cap. |
7 numbers |
10 |
10 |
30 total |
|
Mult. speed |
4 sec. |
1 sec. |
1 sec. |
0.8 sec. |
|
Mult. method |
repeated add. |
table look-up |
table look-up |
rep. add. |
|
Cost |
. |
$65,000 |
$65,000 |
$500,000 |
|
Size |
2 panels |
5 panels |
5 panels |
27 panels |
Table: The Model II – Model V Relay
Computers [R09]
The Model V was a powerful machine, in many ways more reliable than and just as powerful as the faster electronic computers of its time. The relay computers became obsolete because the Model V represented the basic limit of the relay technology, whereas the electronic computers could be modified considerably.
The IBM Series 400
Accounting Machines
We now examine another branch of electromechanical computing devices that existed before 1940 and influenced the development of the early digital computers. This is a family of accounting machines produced by the International Business Machines Corporation (IBM), beginning with the IBM 405 Alphabetical Accounting Machine, introduced in 1934.

Figure: IBM
Type 405 [R55]
According to the reference [R55], the IBM 405 was IBM's high-end tabulator offering (and the first one to be called an Accounting Machine).The 405 was programmed by a removable plugboard with over 1600 functionally significant "hubs", with access to up to 16 accumulators, the machine could tabulate at a rate of 150 cards per minute, or tabulate and print at 80 cards per minute. The print unit contained 88 type bars, the leftmost 43 for alphanumeric characters and the other 45 for digits only. The 405 was IBM's flagship product until after World War II (in which the 405 was used not only as a tabulator but also as the I/O device for classified relay calculators built by IBM for the US Army). In 1948, the Type 405 was replaced by an upgraded model, called the Type 402.

Figure: The type bars of an IBM 402
Accounting Machine [R55]
As noted above, the IBM 405 and its successor, the IBM 402, were programmed by wiring plugboards. In order to facilitate the use of “standard programs”, the plugboard included a removable wiring unit upon which a standard wiring could be set up and saved.

Figure: The
Plugboard Receptacle

Figure: A Wired
Plugboard
The Harvard Computers: Mark I, Mark II, Mark III, and Mark IV
The Harvard Mark I, also known as the IBM Automatic Sequence Controlled Calculator (ASCC) was the largest electromechanical calculator ever built. It has a length of 51 feet, a height of eight feet, and weighed nearly five tons. Here is a picture of the computer, from the IBM archives (http://www-1.ibm.com/ibm/history/exhibits/markI/markI_intro.html).

Figure: The Harvard Mark I
This
computer was conceived in the 1930’s by Howard H. Aiken, then a graduate
student in theoretical physics at
The Mark I operated at Harvard for 15 years, after which the machine was broken up and parts sent to the Smithsonian museum, a museum at Harvard, and IBM’s collection. It was the first of a sequence of four electromechanical computers that lead up to the ENIAC.
The Mark II was begun in 1942 and completed in 1947. The Mark III, completed in 1949, was the first of the series to use an internally stored program and indirect addressing. The Mark IV, last of this series, was completed in 1952. It had a magnetic core memory used to store 200 registers and seems to have used some vacuum tubes as well.
IBM describes the Mark I, using its name “ASCC” (Automatic Sequence Controlled Calculator) in its archive web site, as
“consisting of 78 adding machines and calculators linked together, the ASCC had 765,000 parts, 3,300 relays, over 500 miles of wire and more than 175,000 connections. The Mark I was a parallel synchronous calculator that could perform table lookup and the four fundamental arithmetic operations, in any specified sequence, on numbers up to 23 decimal digits in length. It had 60 switch registers for constants, 72 storage counters for intermediate results, a central multiplying-dividing unit, functional counters for computing transcendental functions, and three interpolators for reading function punched into perforated tape.”
The Harvard Mark II, the second in the sequence of electromechanical computers, was also built by Howard Aiken with support from IBM. In 1945 Grace Hopper was testing the Harvard Mark II when she made a discovery that has become historic – the “first computer bug”, an occurrence reported in her research notebook, a copy of which is just below.

Source: Naval
The caption associated with the moth picture on the web site is as follows.
“Moth found trapped
between points at Relay # 70, Panel F, of the Mark II Aiken Relay Calculator
while it was being tested at
“In 1988, the log,
with the moth still taped by the entry, was in the
We should note that this
event is not the first occurrence of the use of the word “bug” to reference a
problem or error. The term was current
in the days of Thomas A. Edison, the great American inventor. One meaning of the word “bug” as defined in the
second edition of the Oxford English Dictionary is “A defect or fault in a
machine, plan, or the like, origin
“Mr. Edison, I was informed, had been up the two previous nights discovering ‘a bug’ in his phonograph – an expression for solving a difficulty and implying that some imaginary insect has secreted itself inside and is causing all the trouble.”
The Colossus
The Colossus was a computer built in

Figure: The Colossus
The reader should note the paper tape reels at the right of the picture.
Konrad Zuse (1910 – 1995) and the Z Series of Computers
Although he himself claimed
not to have been familiar with the work of Charles Babbage, Konrad Zuse can be
considered to have picked up where Babbage left off. Zuse used electromechanical relays instead of
the mechanical gears that Babbage had chosen.
Zuse built his first computer, the Z1, in his parent’s
After the war, Zuse was
employed in the
Z1 (1938), a mechanical programmable digital computer. Although mechanical problems made its operation erratic, it was rebuilt by Zuse himself after the war.
Z2 (1940), an electro-mechanical computer.
Z3 (1941), this
machine uses program control.
Plankalkül (1945/46), the first programming language, implemented on the Z3.
Z22 (1958), the last machine developed by Zuse. It was one of the first to be designed with transistors
The next figure shows the
rebuilt Z1 in the

Figure: Konrad Zuse and the Reconstructed Z1
Source: R29
We use some of Konrad Zuse’s own memoirs to make the transition to our discussion of the “first generation” of computers – those based on vacuum tube technology. Zuse begins with a discussion of Helmut Schreyer, a friend of his who first had the idea.
“Helmut was a high-frequency engineer, and on completing his studies (around 1936) … suddenly had the bright idea of using vacuum tubes. At first I thought it was one of his student pranks - he was always full of fun and given to fooling around. But after thinking about it we decided that his idea was definitely worth a try. Thanks to switching algebra, we had already married together mechanics and electro-magnetics – two basically different types of technology. Why, then, not with tubes? They could switch a million times faster than elements burdened with mechanical and inductive inertia.”
“The possibilities were staggering. But first basic circuits for the major logical operations such as conjunction, disjunction and negation had to be discovered. Tubes could not simply be connected in line like relay contacts. We agreed that Helmut should develop the circuits for these elementary operations first, while I dealt with the logical part of the circuitry. Our aim was to set up elementary circuits so that relay technology could be transferred to the tube system on a one-to-one basis. This meant the tube machine would not have to be redesigned from scratch. Schreyer solved this problem fairly quickly.”
“This left the way open for further development. We cautiously told some friends about the possibilities. The reaction was anything from extremely skeptical to spontaneously enthusiastic. Interestingly enough, most criticism came from Schreyer's colleagues, who worked with tubes virtually all the time. They were doubtful that an apparatus with 2,000 tubes would work reliably. This critical attitude was the result of their own experience with large transmitters which contained several hundred tubes.”
“After the War was finally over, news of the
Vacuum Tube Computers
(Generation 1 – from 1945 to 1958)
It is now generally conceded
that the first purely electronic binary digital computer was designed by John
Vincent Atanasoff (October 4, 1903 – June 15, 1995) at
The relation of the ABC to the ENIAC (once claimed to be the first electronic digital computer) has been the source of much discussion. In fact, the claim of precedence of the ABC over the ENIAC was not settled until taken to court quite a bit later.

Figure: Clifford Berry standing in front of
the ABC
Source: R31
Atanasoff [R 32] decided in building the ABC that:
“1) He would use electricity and electronics as the medium for the
computer.
2) In spite of custom, he would use
base-two numbers (the binary system)
for his computer.
3) He would use condensers (now called
“capacitors” – see Review of Basic
Electronics in these notes) for
memory and would use a regenerative or
"jogging" process to
avoid lapses that might be caused by leakage of power.
4) He would compute by direct logical
action and not by enumeration as
used in analog calculating
devices.”
According to present-day supporters of Dr. Atanasoff, two problems prevented him from claiming the credit for creation of the first general-purpose electronic digital computer: the slow process of getting a patent and attendance at a lecture by Dr. John Mauchly, of ENIAC fame. In 1940, Atanasoff attended a lecture given by Dr. Mauchly and ,after the lecture, spent some time discussing electronic digital computers with him. This lead to an offer to show Mauchly the ABC; it was later claimed that Mauchly used many of Atanasoff’s ideas in the design of the ENIAC without giving proper credit.
Atanasoff sued Mauchly in U.S. Federal Court, charging him with piracy of intellectual property. This trail was not concluded until 1972, at which time U.S. District Judge Earl R. Larson ruled that the ENIAC was "derived" from the ideas of Dr. Atanasoff. While Mauchly was not deemed to have stolen Atanasoff’s ideas, the judge did give Atanasoff credit as the inventor of the electronic digital computer. [R32]
As we shall see below, the claim of the ENIAC as the first electronic digital computer is not completely unfair to Dr. Atanasoff; it is just not entirely true.