Chapter 7 Appendix – Design of the 11011 Sequence Detector

Design of Sequential Circuits

We now do the 11011 sequence detector as an example. We begin with the formal problem statement, repeat the design rules, and then apply them.

A sequence detector accepts as input a string of bits: either 0 or 1. Its output goes to 1 when a target sequence has been detected. There are two basic types: overlap and non-overlap. In an sequence detector that allows overlap, the final bits of one sequence can be the start of another sequence. Our example will be a 11011 sequence detector. It raises an output of 1 when the last 5 binary bits received are 11011. At this point, a detector with overlap will allow the last two 1 bits to serve at the first of a next sequence. By example we show the difference between the two detectors. Suppose an input string 11011011011.

11011 detector with overlap X 11011011011

Z 00001001001

11011 detector with no overlap Z 00001000001

The sequence detector with no overlap allowed resets itself to the start state when the sequence has been detected. Write the input sequence as 11011 011011. After the initial sequence 11011 has been detected, the detector with no overlap resets and starts searching for the initial 1 of the next sequence. The detector with overlap allowed begins with the final 11 of the previous sequence as ready to be applied as the first 11 of the next sequence; the next bit it is looking for is the 0.

Here is an overview of the design procedure for a sequential circuit.

1) Derive the state diagram and state table for the circuit.
2) Count the number of states in the state diagram (call it N) and calculate the
number of flip-flops needed (call it P) by solving the equation
2^P-1 < N £ 2^P. This is best solved by guessing the value of P.
3) Assign a unique P-bit binary number (state vector) to each state.
Often, the first state = 0, the next state = 1, etc.
4) Derive the state transition table and the output table.
5) Separate the state transition table into P tables, one for each flip-flop.
WARNING: Things can get messy here; neatness counts.
6) Decide on the types of flip-flops to use. When in doubt, use all JK’s.
7) Derive the input table for each flip-flop using the excitation tables for the type.
8) Derive the input equations for each flip-flop based as functions of the input
and current state of all flip-flops.
9) Summarize the equations by writing them in one place.
10) Draw the circuit diagram. Most homework assignments will not go this far,
as the circuit diagrams are hard to draw neatly.

Problem: Design a 11011 sequence detector using JK flip-flops. Allow overlap.

Step 1 – Derive the State Diagram and State Table for the Problem

The method to be used for deriving the state diagram depends on the problem. I show the method for a sequence detector. At this point in the problem, the states are usually labeled by a letter, with the initial state being labeled “A”, etc.

Step 1a – Determine the Number of States

It can be proven that an N-bit sequence detector requires at least N states to function correctly. It can also be shown that a circuit with more than N states is unnecessarily complicated and a waste of hardware; thus, an N-bit sequence detector has N states.

We are designing a sequence detector for a 5-bit sequence, so we need 5 states. We label these states A, B, C, D, and E. State A is the initial state.

Step 1b – Characterize Each State by What has been Input and What is Expected

State Has Awaiting
A -- 11011

B 1 1011

C 11 011

D 110 11

E 1101 1

Step 1c – Do the Transitions for the Expected Sequence

Here is a partial drawing of the state diagram. It has only the sequence expected. Note that the diagram returns to state C after a successful detection; the final 11 are used again.

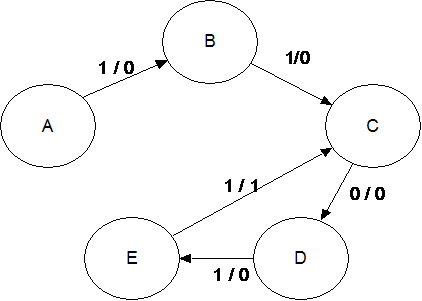
Note the labeling of the transitions: X / Z. Thus the expected transition from A to B has an input of 1 and an output of 0.

The transition from E to C has an output of 1 denoting that the desired sequence has been detected.

Step 1d – Insert the Inputs That Break the Sequence

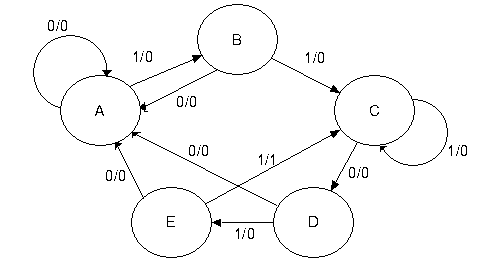
Each state has two lines out of it – one line for a 1 and another line for a 0.

The notes below explain how to handle the bits that break the sequence.

A State A is the initial state. It is waiting on a 1. If it gets a 0, the machine remains
in state A and continues to remain there while 0’s are input.

B If state B gets a 0, the last two bits input were “10”. This does not begin the
sequence, so the machine goes back to state A and waits on the next 1.
C If state C gets a 1, the last three bits input were “111”. It can use the last two
of these 1’s to be the first two 1’s of the sequence 11011, so the machine stays
in state C awaiting a 0. We might have something like 1111011, etc.

D If state D gets a 0, the last four bits input were 1100. These 4 bits are not part of
the sequence, so we start over.
E If state E gets a 0, the last five bits input were 11010. These five bits are not part of the
sequence, so start over.

More precisely we should be discussing prefixes and suffixes. At state C with input 111, the two bit suffix to the sequence input is 11 which is a two bit prefix of the desired sequence, so we stay at C. At E, getting a sequence 11010, we note that the 1-bit suffix is a 0, which is not a prefix of the desired sequence, the 2-bit suffix is 10, also not a prefix, etc.

Step 1e – Generate the State Table with Output

Present State	Next State / Output
	X = 0	X = 1
A	A / 0	B / 0
B	A / 0	C / 0
C	D / 0	C / 0
D	A / 0	E / 0
E	A / 0	C / 1

Step 2 – Determine the Number of Flip-Flops Required

We have 5 states, so N = 5. We solve the equation 2^P-1 < 5 £ 2^P by inspection, noting that it is solved by P = 3. So we need three flip-flops.

Step 3 – Assign a unique P-bit binary number (state vector) to each state.

The simplest way is to make the following assignments
A = 000
B = 001
C = 010
D = 011
E = 100

Occasionally, a better assignment can be detected by inspection of the next state table. I note that the next states in the table cluster into two disjoint sets for X = 0 and X = 1.
For X = 0 the possible next states are A and D
For X = 1 the possible next states are B, C, and E.

For this reason, I elect to give even number assignments to states A and D, and to give odd number assignments to states B, C, and E. Being somewhat traditional, I want to assign the state numbers in increasing order so that we don’t get totally confused. The assignment is
A = 000
B = 001
C = 011 Note that states 010, 110, and 111 are not used.
D = 100
E = 101

Step 4 – Generate the Transition Table With Output

Note that in many designs, such as counters, the states are already labeled with binary numbers, so the state table is the transition table. We shall label the internal state by the three bit binary number Y₂Y₁Y₀ and use the three-bit vectors defined above.

Present State		Next State / Output
		X = 0	X = 1
	Y2Y1Y0	Y2Y1Y0 / Z	Y2Y1Y0 / Z
A	0 0 0	0 0 0 / 0	0 0 1 / 0
B	0 0 1	0 0 0 / 0	0 1 1 / 0
C	0 1 1	1 0 0 / 0	0 1 1 / 0
D	1 0 0	0 0 0 / 0	1 0 1 / 0
E	1 0 1	0 0 0 / 0	0 1 1 / 1

Step 4a – Generate the Output Table and Equation

The output table is generated by copying from the table just completed.

Present State	X = 0	X = 1
Y2Y1Y0	0	0
0 0 0	0	0
0 0 1	0	0
0 1 1	0	0
1 0 0	0	0
1 0 1	0	1

The output equation can be obtained from inspection.
As is the case with most sequence detectors, the
output Z is 1 for only one combination of present state
and input. Thus we get Z = X · Y₂ · Y₁’ · Y₀.

This can be simplified by noting that the state 111 does
not occur, so the answer is Z = X · Y₂ · Y₀.

Step 5 – Separate the Transition Table into Three Tables, One for Each Flip-Flop

We shall generate a present state / next state table for each of the three flip-flops; labeled Y₂, Y₁, and Y₀. It is important to note that each of the tables must include the complete present state, labeled by the three bit vector Y₂Y₁Y₀.

Y2			Y1			Y0
PS	Next State		PS	Next State		PS	Next State
Y2Y1Y0	X = 0	X = 1	Y2Y1Y0	X = 0	X = 1	Y2Y1Y0	X = 0	X = 1
0 0 0	0	0	0 0 0	0	0	0 0 0	0	1
0 0 1	0	0	0 0 1	0	1	0 0 1	0	1
0 1 1	1	0	0 1 1	0	1	0 1 1	0	1
1 0 0	0	1	1 0 0	0	0	1 0 0	0	1
1 0 1	0	0	1 0 1	0	1	1 0 1	0	1

Match Y₁ Y₂·Y₀’ 0 Y₀ 0 1

Before trying step 6, I shall note a quick, but often messy, implementation. We look at an implementation using D flip-flops only. For each flip-flop, we have the desired next state for each combination of present state and input. Remember that the D flip-flop equation is
D = Q(T + 1); i.e., input to the flip-flop whatever the next state is to be. Thus, this design is

D₂ = X’·Y₁ + X·Y₂·Y₀’

D₁ = X ·Y₀

D₀ = X

While this may be an acceptable implementation, it is important to complete the original design problem using JK flip-flops. What we want is input equations for J₂, K₂, J₁, K₁,
J₀, and K₀. Inspection of the above gives little clue for the first two flip-flops, but any student recalling the use of a JK flip-flop to implement a D flip-flop will see immediately that the input equation for flip-flop 0 is J₀ = X and K₀ = X’.

Step 6 – Decide on the type of flip-flops to be used.

The problem stipulates JK flip-flops, so we use them. As an aside, we examine the difficulties of designing the circuit with D flip-flops.

Step 7 – Derive an Input Table for Each Flip-Flop using its Excitation Table

and

Step 8 – Produce the Input Equations for Each Flip-Flop

It is at this point that we first use the fact that we have specified JK flip-flops for the design. We have already considered a D flip-flop implementation. Because we are using JK flip-flops, we show the excitation table for a JK flip-flop.

Q(T) Q(T + 1) J K

0 0 0 d We shall see shortly how the presence of the

0 1 1 d d (Don’t Care) state simplifies design.

1 0 d 1

1 1 d 0

It is at this point that neatness counts. For each flip-flop we shall write out the complete present state and the next state of the specific flip-flop. We then use the present state and next state of the specific flip-flop to determine its required input. The problem here is comparing the next state of the flip-flop to the correct present state.

Y2Y1Y0	X = 0			X = 1
	Y2	J2	K2	Y2	J2	K2
0 0 0	0	0	d	0	0	d
0 0 1	0	0	d	0	0	d
0 1 1	1	1	d	0	0	d
1 0 0	0	d	1	1	d	0
1 0 1	0	d	1	0	d	1

First we do Y₂.

Probably the easiest way to generate this table is to do all of the “0 to 0” transitions first, then the “0 to 1”, etc. For this flip-flop, be sure to refer back to the Y₂ part of the PS.

We now try to produce the input equations for J₂ and K₂ by simplifying the above columns. The best way is to consider first the X = 0 columns, then the X = 1 columns and finally to combine the two. There are formal ways to do this, but I try simple matching.

1) If a column has only 0 and d, it is matched by 0.
2) If a column has only 1 and d, it is matched by 1.
3) If this does not work, try a match to one of Y₂, Y₁, or Y₀.
Remember, the d entries do not have to match anything.

Consider X = 0. In the above, for J₂, we have only 001 as a real pattern. These copy the pattern seen in Y₁, so we make the assignment that for X = 0, J₂ = Y₁. For X = 0, the only pattern seen is a pair of 1’s, so for X = 0 we set K₂ = 1.

X = 0 X = 1

J₂ = Y₁ J₂ = 0 thus, J₂ = X’·Y₁
K₂ = 1 K₂ = Y₀ thus, K₂ = X’ + X·Y₀ = X’ + Y₀.

Note the combination rule X’·(expression for X= 0) + X·(expression for X = 1).

Applied to J₂, the rule gives J₂ = X’·Y₁ + X·0 = X’·Y₁

The second simplification uses the absorption law: X’ + X·Y = X’ + Y for any X and Y.

We now derive the input equations for flip-flop 1.

Y2Y1Y0	X = 0			X = 1
	Y1	J1	K1	Y1	J1	K1
0 0 0	0	0	d	0	0	d
0 0 1	0	0	d	1	1	d
0 1 1	0	d	1	1	d	0
1 0 0	0	0	d	0	0	d
1 0 1	0	0	d	1	1	d

The patterns are detected first for X = 0 and X = 1 separately and then combined.

X = 0 X = 1

J₁ = 0 J₁ = Y₀

K₁ = 1 K₁ = 0 thus J₁ = X·Y₀ and K₁ = X’.

We now derive the input equations for flip-flop 0.

Y2Y1Y0	X = 0			X = 1
	Y0	J0	K0	Y0	J0	K0
0 0 0	0	0	d	1	1	d
0 0 1	0	d	1	1	d	0
0 1 1	0	d	1	1	d	0
1 0 0	0	0	d	1	1	d
1 0 1	0	d	1	1	d	0

The patterns are detected as above

X = 0 X = 1

J₀ = 0 J₀ = 1

K₀ = 1 K₀ = 0 thus J₀ = X and K₀ = X’, as expected.

Step 9 – Summarize the Equations

The purpose of this step is to place all of the equations into one location and facilitate grading by the instructor. Basically we already have all of the answers.

Z = X·Y₂·Y₀

J₂ = X’·Y₁ and K₂ = X’ + Y₀

J₁ = X·Y₀ and K₁ = X’

J₀ = X and K₀ = X’

Step 10 – Draw the Circuit

I usually do not ask for this step as it tends to be messy and is always hard to grade.

The figure on the next page has been added to show a typical drawing of this circuit as implemented by JK flip-flops.

Here is the circuit for the 11011 sequence detector as implemented with JK flip-flops.

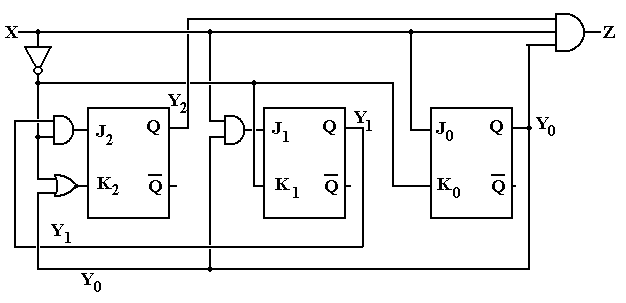
The equations implemented in this design are:

Z = X·Y₂·Y₀

J₂ = X’·Y₁ K₂ = X’ + Y₀

J₁ = X·Y₀ K₁ = X’

J₀ = X K₀ = X’

Here is the same design implemented with D flip-flops.

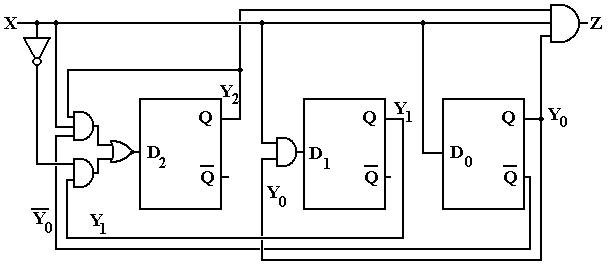
The equations for this design are D₂ = X’·Y₁ + X·Y₂·Y₀’

D₁ = X ·Y₀

D₀ = X

More on Overlap – What it is and What it is not

At this point, we need to focus more precisely on the idea of overlap in a sequence detector. For an extended example here, we shall use a 1011 sequence detector.

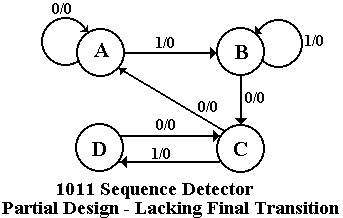
The next figure shows a partial state diagram for the sequence detector. The final transitions from state D are not specified; this is intentional.

Here we focus on state C and the X=0 transition coming out of state D. By definition of the system states,

State C – the last two bits were 10

State D – the last three bits were 101.

If the system is in state D and gets a 0 then the last four bits were 1010, not the desired sequence. If the last four bits were 1010, the last two were 10 – go to state C. The design must reuse as many bits as possible.

Note that this decision to go to state C when given a 0 is state D is totally independent of whether or not we are allowing overlap. The question of overlap concerns what to do when the sequence is detected, not what to do when we have input that breaks the sequence.

Just to be complete, we give the state diagrams for the two implementations of the sequence detector – one allowing overlap and one not allowing overlap.

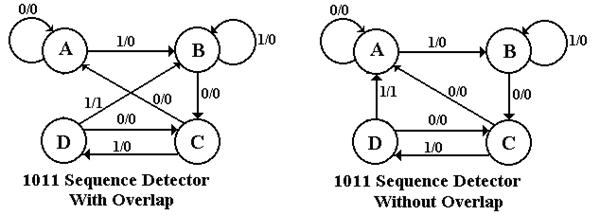
The student should note that the decision on overlap does not affect designs for handling partial results – only what to do when the final 1 in the sequence 1011 is detected.