What Is It?

Consider the following set of 32 binary digits, written in blocks of four
so that the example is not impossible to read.

0010 0110 0100 1100 1101 1001 1011 1111

How do we interpret this sequence of binary digits?

Answer: The interpretation depends on the use made of the number.
Where is this 32–bit binary number found?

Instruction Register If in the IR, this number will be decoded as an
instruction, probably with an address part.

Address Register If in the MAR or another address register, this
is a memory address.

Data Register If in a general purpose (data) register, this is data.

Possibly a 32–bit real number
Possibly a 32–bit integer
Possibly four 8–bit character codes.

Hexadecimal Numbers

But first, we present a number system that greatly facilitates writing long
strings of binary numbers. This is the hexadecimal system.

The hexadecimal system (base 16 = 2⁴) has 16 digits, the normal ten decimal digits and the first six letters of the alphabet.

Because hexadecimal numbers have base 2⁴, each hexadecimal digit represents four binary bits. Hexadecimal notation is a good way to write binary numbers.

The translation table from hexadecimal to binary is as follows.

0 0000 4 0100 8 1000 C 1100
1 0001 5 0101 9 1001 D 1101
2 0010 6 0110 A 1010 E 1110
3 0011 7 0111 B 1011 F 1111

Consider the previous example

0010 0110 0100 1100 1101 1001 1011 1111

As a hexadecimal number it is 264CD9BF, better written as 0x264C D9BF.
The “0x” is the standard C++ and Java prefix for a hexadecimal constant.

Conversions between Hexadecimal and Binary

These conversions are particularly easy, due to the fact that the base of
hexadecimal numbers is a power of two, the base of binary numbers.

Hexadecimal to Binary
Just write each hexadecimal number as four binary numbers.
String the binary numbers together in a legible form.

Binary to Hexadecimal
Group the binary bits by fours.
Add leading zeroes to the leftmost grouping of binary bits, so that
all groupings have exactly four binary bits.
Convert each set of four bits to its hexadecimal equivalent.
Write the hexadecimal number. It is better to use the “0x” prefix.

The numbering system is often called “Hex”.

Early proponents of computer security noted many similarities between their subject and that of disease prevention, called for “safe hex”.

Three Number Systems

This course is built upon three number systems and conversions between them.

Binary Base 2 Digit set = {0, 1}

Decimal Base 10 Digit set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Hexadecimal Base 16 Digit set = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

We shall discuss five of the six possible conversion algorithms.

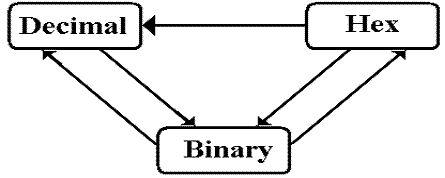
I don’t know a good algorithm for direct conversion from decimal to hexadecimal, so I always use binary as an intermediate point.

Octal (base 8) notation is useful in certain applications, but we won’t study it.

Other number systems, such as base 5 and base 7, are useless teaching devices.

Binary, Decimal, and Hexadecimal Equivalents

Binary Decimal Hexadecimal

0000 0 0

0001 1 1

0010 2 2

0011 3 3

0100 4 4

0101 5 5

0110 6 6

0111 7 7

1000 8 8

1001 9 9

1010 10 A

1011 11 B

1100 12 C

1101 13 D

1110 14 E

1111 15 F

Conversion between Binary and Hexadecimal

This is easy, just group the bits. Recall that
A = 1010 B = 1011 C = 1100
D = 1101 E = 1110 F = 1111

Problem: Convert 10011100 to hexadecimal.
1. Group by fours 1001 1100
2. Convert each group of four 0x9C

Problem: Convert1111010111 to hexadecimal.
1. Group by fours (moving right to left) 11 1101 0111
Add leading zeroes 0011 1101 0111
2. Convert each group of four 0x3D7

Problem: Convert 0xBAD1 to binary
1. Convert each hexadecimal digit: B A D 1
1011 1010 1101 0001

2. Group the binary bits 1011101011010001

Conversion from Hexadecimal to Decimal

Remember (or calculate) the needed powers of sixteen, in decimal form.

16⁰ = 1 16¹ = 16 16² = 256 16³ = 4096 16⁴ = 65536, etc.

1. Convert all of the hexadecimal digits to their decimal form.
This affects only the digits in the set {A, B, C, D, E, F}

2. Use standard positional conversion.

Example: 0xCAFE

Convert each digit 12 10 15 14

Positional conversion 12·16³ + 10·16² + 15·16¹ + 14·16⁰ =

12·4096 + 10·256 +15·16 + 14·1 =

49,152 + 2,560 + 240 + 14 = 51,966

NOTE: Java class files begin with the following 32–bit (8 hex digit) identifier
CAFE BABE.
This is an inside joke among the Java development team.

Conversion between Binary and Decimal

Conversion between hexadecimal and binary is easy because 16 = 2⁴.
In my view, hexadecimal is just convenient “shorthand” for binary.
Thus, four hex digits stand for 16 bits, 8 hex digits for 32 bits, etc.

But 10 is not a power of 2, so we must use different methods.

Conversion from Binary to Decimal

This is based on standard positional notation.

Convert each “position” to its decimal equivalent and add them up.

Conversion from Decimal to Binary

This is done with two distinct algorithms, one for the digits to the left of
the decimal point (the whole number part) and one for digits to the right.

At this point we ignore negative numbers.

Powers of Two

Students should memorize the first ten powers of two.

2⁰ = 1
2¹ = 2 2^–1 1/2 = 0.5
2² = 4 2^–2 1/4 = 0.25
2³ = 8 2^–3 1/8 = 0.125

2⁴ = 16 2^–4 1/16 = 0.0625
2⁵ = 32 2^–5 1/32 = 0.03125
2⁶ = 64 2^–6 1/64
2⁷ = 128 2^–7 1/128
2⁸ = 256 2^–8 1/256
2⁹ = 512 2^–9 1/512
2¹⁰ = 1024 2^–10 1/1024 » 0.001

10111.011 = 1·2⁴ + 0·2³ + 1·2² + 1·2¹ + 1·2⁰ + 0·2^-1 + 1·2^-2 + 1·2^-3

= 1·16 + 0·8 + 1·4 + 1·2 + 1·1 + 0·0.5 + 1·0.25 + 1·0.125
= 23.375

Conversion of Unsigned Decimal to Binary

Again, we continue to ignore negative numbers.

Problem: Convert 23.375 to binary. We already know the answer.

One solution.

23.375 = 16 + 4 + 2 + 1 + 0.25 + 0.125
= 1·2⁴ + 0·2³ + 1·2² + 1·2¹ + 1·2⁰ + 0·2^-1 + 1·2^-2 + 1·2^-3
= 10111.011

This solution is preferred by your instructor, but most students find it
confusing and opt to use the method to be discussed next.

Side point: Conversion of the above to hexadecimal involves grouping
the bits by fours as follows:
Left of decimal: by fours from the right
Right of decimal: by fours from the left.

Thus the number is 1 0111.011 = 0001 0111.0110 or 0x17.6

But 0x17.6 = 1·16 + 7·1 + 6/16 = 23 + 3/8 = 23.375

Conversion of the “Whole Number” Part

This is done by repeated division, with the remainders forming the binary
number. This set of remainders is read “bottom to top”

Quotient Remainder

23/2 = 11 1 Thus decimal 23 = binary 10111

11/2 = 5 1

5/2 = 2 1 Remember to read the binary

2/2 = 1 0 number from bottom to top.

1/2 = 0 1 As expected, the number is 10111

Another example: 16

Quotient Remainder

16/2 = 8 0

8/2 = 4 0

4/2 = 2 0 Remember to read the binary

2/2 = 1 0 number from bottom to top.

1/2 = 0 1 The number is 10000 or 0x10

Convert the Part to the Right of the Decimal

This is done by a simple variant of multiplication.
This is easier to show than to describe. Convert 0.375

Number Product Binary

0.375 x 2 = 0.75 0

0.75 x 2 = 1.5 1 Read top to bottom as .011

0.5 x 2 = 1.0 1

Note that the multiplication involves dropping the leading ones from the product terms, so that our products are 0.75, 1.5, 1.0, but we would multiply only the numbers 0.375, 0.75, 0.50, and (of course) 0.0.

Another example: convert 0.71875

Number Product Binary
0.71875 x2 = 1.4375 1
0.4375 x 2 = 0.875 0 Read top to bottom as .10111
0.875 x 2 = 1.75 1 or as .1011100000000 …
0.75 x 2 = 1.5 1 with as many trailing zeroes as you like
0.5 x 2 = 1.0 1
0.0 x 2 = 0.0 0

Convert an “Easy” Example

Consider the decimal number 0.20. What is its binary representation?

Number Product Binary

0.20 · 2 = 0.40 0
0.40 · 2 = 0.80 0

0.80 · 2 = 1.60 1

0.60 · 2 = 1.20 1

0.20 · 2 = 0.40 0

0.40 · 2 = 0.80 0

0.80 · 2 = 1.60 1 but we have seen this – see four lines above.

So 0.20 decimal has binary representation .00 1100 1100 1100 ….

Terminating and Non–Terminating Numbers
A fraction has a terminating representation in base–K notation only if the number can be represented in the form J / (B^K)

Thus the fraction 1/2 has a terminating decimal representation because it is
5 / (10¹). It can also be 50 / (10²), etc. Also 1/4 = 25 / (10²), 1/8 = 125/(10³).

More on Non–Terminators

What about a decimal representation for 1/3?

If we can generate a terminating decimal representation, there must be positive integers J and K such that 1 / 3 = J / (10^K). But 10 = 2·5, so this becomes

1 / 3 = J / (2^K · 5^K).

Cross multiplying, and recalling that everything is a positive integer, we have

3·J = (2^K · 5^K)

If the equation holds, there must be a “3” on the right hand side. But there cannot be a “3” on this side, as it is only 2’s and 5’s.

Now, 0.20 = 1 / 5 has a terminating binary representation only if it has a representation of the form J / (2^K).

This becomes 1 / 5 = J / (2^K), or 5·J = 2^K. But no 5’s on the RHS.

Because numbers such as 1.60 have no exact binary representation, bankers and others who rely on exact arithmetic prefer BCD arithmetic, in which exact representations are possible.