Two’s Complement Arithmetic

We now address the issue of representing integers as binary strings in a computer.

There are four formats that have been used in the past; only one is of interest to us.

The four formats are

1. Sign–Magnitude

2. One’s–Complement

3. Two’s–Complement

4. Excess–N, where N is some positive integer; say 127 for Excess–127.

Sign–magnitude representation is obsolete.

Excess–127 representation is only used as part of floating point representations.
If discussed at all, it will be in the context of the IEEE–754 standard.

We focus on Two’s–complement, but discuss one’s–complement arithmetic as
a mechanism for generating the two’s complement.

Representation of Non–Negative Integers

In each of one’s–complement and two’s–complement arithmetic, no special steps
are required to represent a non–negative integer.

All conversions to the complement number systems begin with conversion to simple
binary representation, often from decimal notation.

The only issue with non–negative integers is to insure that the number is not too large
for the number of bits used in the representation.

There are two ways to define this size limitation in the complement numbers system.
1. The most significant bit (leftmost) must be a “0” for non–negative numbers.
2. For an N–bit representation, the number must be less than 2^N–1.

The biggest signed 8–bit integer is 2⁷ – 1 = 127.
The biggest signed 16–bit integer is 2¹⁵ – 1 = 32767.

Three 8–bit examples: 100 = 0110 0100
22 = 0001 0110
0 = 0000 0000

Leading Zeroes Are Significant

When we talk about any number system that can represent signed integers, we must
specify the number of bits used to represent the number.

Each binary representation must have that number of bits. This means padding
non–negative numbers with leading zeroes.

Thus, we could say 100 = 110 0100
22 = 1 0110
0 = 0.

But, when we discuss 8–bit numbers, we MUST SAY
100 = 0110 0100
22 = 0001 0110
0 = 0000 0000

The common integer sizes for signed arithmetic are 8–bit, 16–bit, and 32–bit.

I have worked with 12–bit, 18–bit, 30–bit, and 36–bit signed integers.
These are of interest only for assigning problems to students.

Taking the One’s–Complement

To take the one’s complement of a binary integer, just
Change every 0 to a 1
Change every 1 to a 0

One’s–complement arithmetic is that arithmetic that uses the one’s–complement of
a binary integer to represent its negative.

+ 100 in 8–bit one’s complement. 0110 0100.

– 100 in 8–bit one’s complement.
Convert 100 to 8–bit binary 0110 0100
Take the one’s complement 1001 1011
– 100 is represented as 1001 1011

+ 22 is 8–bit one’s complement 0001 0110

– 22 in 8–bit one’s complement
Convert 22 to 8–bit binary 0001 0110
Take the one’s complement 1110 1001
– 22 is represented as 1110 1001

We no longer use one’s–complement arithmetic. It has two serious problems.

Problems with One’s–Complement Arithmetic

There are two serious problems with the use of one’s–complement arithmetic. The first one will be described but not explained.

Problem 1: It is a lot trickier to build a binary adder for one’s–complement numbers.
Just take my word for this one.

Problem 2: Negative Zero

Consider 8–bit one’s–complement arithmetic

+ 0 is 0000 0000

Take the one’s complement 1111 1111

So – 0 is represented by 1111 1111

Most of us are uneasy about having a distinct – 0 in our number system.

Code such as the following is considered strange.
if ( ( x == 0) || (x == –0) )

This course will not cover one’s–complement arithmetic or use it directly for any purpose other than taking the two’s complement, discussed next.

Taking the Two’s Complement

There are two processes for taking the two’s complement of a number. The one that students find the most natural involves first taking the one’s complement and then adding
1 to that complement.

We must then cover the addition of two binary bits, specifically mentioning each of the
sum bits and carry bits. The analog in decimal arithmetic is to say that the sum of 5 and 5 is 0 with a carry of 1. Yes, 5 + 5 = 10, generating two digits from 2 one–digit numbers.

Here is the binary addition table

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Yes, 1 + 1 is really 2. We denote this by saying that the sum 1 + 1 carries 1
into the two’s column.

Consider 5 + 7 5 = 0101
7 = 0111
1100 12

Taking the Two’s Complement (Part 2)

The recipe for taking the two’s–complement of a binary number is simple.

1. Take the one’s–complement of the number
2. Add 1 to that complement.

+ 100 in 8–bit two’s–complement binary 0110 0100

– 100 in 8–bit two’s–complement binary
Represent +100 as an 8–bit number 0110 0100
Take the one’s complement 1001 1011
Add 1 1
– 100 is represented as 1001 1100

+ 22 in 8–bit two’s–complement binary 0001 0110

– 22 in 8–bit two’s–complement binary
Represent +22 as an 8–bit number 0001 0110
Take the one’s complement 1110 1001
Add 1 1
– 22 is represented as 1110 1010

Taking the Two’s Complement (Part 3)

+ 0 in 8–bit two’s–complement binary 0000 0000

– 0 in 8–bit two’s–complement binary
Represent +0 as an 8–bit number 0000 0000
Take the one’s complement 1111 1111
Add 1 1 Discard the high carry bit
– 0 is represented as 0000 0000

Claim: – 1 in 8–bit two’s–complement binary is 1111 1111.

– 127 and – 128 in 8–bit two’s–complement binary.

+ 127 in 8–bit two’s–complement binary 0111 1111

– 127 in 8–bit two’s–complement binary
Represent +127 as an 8–bit number 0111 1111
Take the one’s complement 1000 0000
Add 1 1
– 127 is represented as 1000 0001

– 128 is “one less” than – 127, so is represented as 1000 0000

Half Adders and Full Adders

A half adder is an adder with no “carry in”. A full adder is an adder that allows
a “carry in”. For adding two binary numbers, the “carry in” is either 0 or 1.

In decimal arithmetic on integers,
a half adder can be used for adding the units column
a full adder would be used for adding the tens, hundreds, thousands (etc.)
columns as each of these can have a “carry in” from a column to the right.

The terms “half adder” and “full adder” apply only to binary arithmetic.

A full adder can be converted to a half adder by setting its “carry in” to 0.

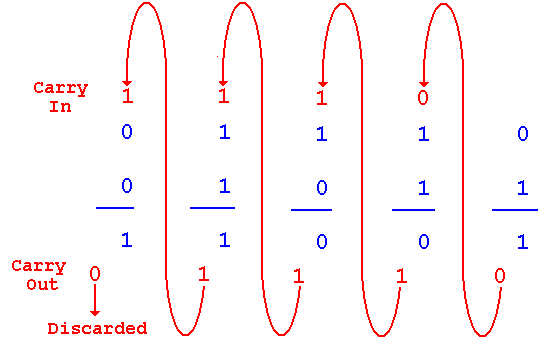
Example From Unsigned Integer Arithmetic

Here we add 14 (binary 01110) and 11 (binary 01011) to get
25 (binary 11001).

Truth Tables for Half Adders and Full Adders

Half-Adder A + B Full-Adder: A + B with Carry In
A B Sum Carry A B C Sum Carry
0 0 0 0 0 0 0 0 0
0 1 1 0 0 0 1 1 0
1 0 1 0 0 1 0 1 0
1 1 0 1 0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

We don’t really need a full adder to do two’s complement arithmetic, but
here it is.

Back to algebra. We were taught that – ( – X) = X for all numbers.
Let’s test it out for two’s–complement arithmetic.

Double Negations (Part 1)

Remember that the range of 8–bit two’s–complement arithmetic is – 128 to 127.

+ 100 in 8–bit two’s–complement binary 0110 0100

– 100 in 8–bit two’s–complement binary
Represent +100 as an 8–bit number 0110 0100
Take the one’s complement 1001 1011
Add 1 1
– 100 is represented as 1001 1100

+100 in 8–bit two’s–complement binary
Represent – 100 as an 8–bit number 1001 1100
Take the one’s complement 0110 0011
Add 1 1
– 100 is represented as 0110 0100

This is the same as + 100. So – ( – 100) is + 100.

Double Negations (Part 2)

Remember that the range of 8–bit two’s–complement arithmetic is – 128 to 127.

+ 22 in 8–bit two’s–complement binary 0001 0110

– 22 in 8–bit two’s–complement binary
Represent +22 as an 8–bit number 0001 0110
Take the one’s complement 1110 1001
Add 1 1
– 22 is represented as 1110 1010

+22 in 8–bit two’s–complement binary
Represent – 22 as an 8–bit number 1110 1010
Take the one’s complement 0001 0101
Add 1 1
+ 22 is represented as 0001 0110

This is the same as + 22. So – ( – 22) is + 22.

Double Negations (Part 3)

Remember that the range of 8–bit two’s–complement arithmetic is – 128 to 127.

+ 127 in 8–bit two’s–complement binary 0111 1111

– 127 in 8–bit two’s–complement binary
Represent +127 as an 8–bit number 0111 1111
Take the one’s complement 1000 0000
Add 1 1
– 127 is represented as 1000 0001

– 128 is represented as 1000 0000
Take the one’s complement 0111 1111
Add 1 1
– (– 128) is represented as 1000 0000

– ( – 128) is the same as – 128 !!

What happened? The answer is that + 128 cannot be represented in
8–bit two’s–complement arithmetic.

Standard Ranges

Here is the standard Java implementation of Two’s–Complement arithmetic.

In general the range for N–bit two’s–complement arithmetic is

– 2^N–1 to 2^N–1 – 1

Java Type	Number of Bits	Lower Limit	Upper Limit
byte	8	– 128	127
short	16	– 32768	32767
int	32	– 2 147 483 648	2 147 483 647
long	64	– 2^63	2^63 – 1

Log₁₀(2) is about 0.30103. Log₁₀(3) is about 0.47712.

Log₁₀(2⁶³) is about 0.30103 · 63 = 18.9649.

Log₁₀(9) = Log₁₀(3²) = 2·Log₁₀(3) = 2·0.47712 = 0.95424.

As 0.9649 > Log₁₀(9), we conclude that 2⁶³ is bigger than 9·10¹⁸.

Standard Values in N–Bit Two’s Complement Arithmetic
(With Examples for 16–bit integers)

0 is represented by N zeroes 0000 0000 0000 0000

–1 is represented by N ones 1111 1111 1111 1111

– 2^N–1 is represented by a 1
followed by (N – 1) zeroes 1000 0000 0000 0000

The student should memorize these patterns and not bother with
standard conversion techniques when obtaining them.

Technically speaking, the representation of – 2^N–1 cannot be derived by
standard means, as 2^N–1 cannot be represented.

Sign Extension

In two’s complement arithmetic, the leftmost bit is the sign bit.

It is 1 for negative numbers
0 for non–negative numbers

Sign extension is the process of converting a N–bit representation to
a larger format; e.g., a 16–bit number to a 32–bit number.

Example:

+ 100 in 8–bit two’s–complement binary 0110 0100

+ 100 in 16–bit two’s–complement binary 0000 0000 0110 0100

– 100 in 8–bit two’s–complement binary 1001 1100

– 100 in 16–bit two’s–complement binary 1111 1111 1001 1100

Rule – just extend the sign bit to fill the new “high order” bits.

Overflow: “Busting the Arithmetic”

The range of 16–bit two’s–complement arithmetic is

– 32,768 to 32,767

Consider the following addition problem: 24576 + 24576.
Now + 24,576 (binary 0110 0000 0000 0000) is well within the range.

0110 0000 0000 0000 24576
0110 0000 0000 0000 24576
1100 0000 0000 0000 – 16384

What happened?

We had a carry into the sign bit. This is “overflow”. The binary representation
being used cannot handle the result.

NOTE: This works as unsigned arithmetic.
24,576 + 24,576 = 49,152 = 32768 + 16384.

When we design a binary adder for N–bit integers (N > 1), we shall address
the standard method for detecting overflow.

Saturation Arithmetic

Saturation arithmetic is applied to unsigned N–bit integers.

The unsigned range is 0 … 2^N – 1.

N = 8 0 through 255
N = 16 0 through 65535
N = 32 0 through 4,294,967,295

Saturation arithmetic is commonly applied to 8–bit integers used in
computer graphics.

RULES: In addition, if the sum is greater than 2^N – 1, set it to 2^N – 1.
In subtraction, if the number is less than 0, set it to 0.

Examples (8–bit saturation arithmetic)

100 + 100 = 200 128 + 128 = 255
128 + 127 = 255 200 + 200 = 255
255 + 255 = 255

Result: Brightening a bright scene does not accidentally make it dark.