Boolean
Algebra & Digital Logic
Boolean
algebra was developed by the Englishman George Boole, who published the basic
principles in the 1854 treatise An
Investigation of the Laws of Thought on Which to Found the Mathematical
Theories of Logic and Probabilities.
The
applicability to computing machines was discovered by three Americans
Claude Shannon Symbolic Analysis of
Relay and Switching Circuits, 1938.
George Stibitz An employee of Bell Labs, he developed a binary adder
using
mechanical relays in 1937, the model “K 1” adder
because
he built it at home on his kitchen table.
John Atanasoff He was probably the first to use purely electronic relays
(vacuum
tubes) to build a binary adder.
Boolean
algebra is a two–valued algebra based on the constant values denoted as either
FALSE, TRUE
0, 1
The
use of this algebra for computation is based on the fact that binary arithmetic
is based on two values, always
called “0” and “1”.
Basic
Boolean Operators
Boolean
algebra is defined in terms of two constants (defined above), which we
call “0” and “1”. Other courses will call these values “F” and
“T”.
Boolean
algebra is defined in terms of three basic operators, to which we shall add
a useful fourth operator. The three operators are NOT, AND, & OR.
Each
of these three basic operators is implemented by a basic electronic device
called a “logic gate”. We present the gates along with the
definition.
NOT This function takes one
input and produces one output. The gate
is shown
below. The circle at the right end of the triangle
is important.

Algebraically,
this function is denoted f(X) = X’ or f(X) = ![]()
The
evaluation of the function is simple: ![]() = 1 and
= 1 and ![]() = 0.
= 0.
Basic
Boolean Operators (Part 2)
Logic OR
This
is a function of two Boolean variables.
We denote the logical OR of two Boolean variables X and Y by “X + Y”. Some logic books will use “X Ú Y”.
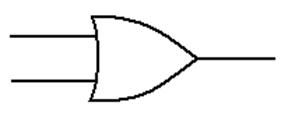
The
evaluation of the logical OR function is shown by a truth table
|
X |
Y |
X + Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Basic
Boolean Operators (Part 3)
Logic AND
This
is a function of two Boolean variables.
We denote the logical AND of two Boolean variables X and Y by “X · Y”. Some logic
books will use “X Ù Y”.
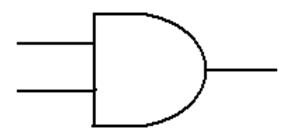
The
evaluation of the logical AND function is shown by a truth table
|
X |
Y |
X · Y |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Another
Boolean Operator
While
not a basic Boolean operator, the exclusive OR is very handy.
Logic XOR
This
is a function of two Boolean variables.
We denote the logical XOR of two Boolean variables X and Y by “X Å Y”. Most logic
books seem to ignore this function.
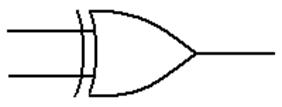
The
evaluation of the logical XOR function is shown by a truth table
|
X |
Y |
X Å Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
From
this last table, we see immediately that
X Å 0 = X and X Å 1 = ![]()
Truth Tables
The
fact that any Boolean variable can assume only one of two possibly values can
be shown, by induction, to imply the following.
For N > 0, N Boolean variables can take only 2N
different combinations of values.
For
small values of N, we can use this to specify a function using a truth table
with 2N rows, plus a header row to label the variables and the
function.
|
N |
2N |
|
1 |
2 |
|
2 |
4 |
|
3 |
8 |
|
4 |
16 |
|
5 |
32 |
|
6 |
64 |
Four–variable
truth tables have 17 rows total. This is
just manageable.
Five–variable truth tables have 33 rows total.
This is excessive.
N–variable truth tables, for N > 5, are almost useless.
Sample Truth
Table
|
A |
B |
C |
F1(A, B, C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
This truth table for 3
variables has 23 = 8 rows, plus a label row.
This
truth table forms a complete definition of the function. We shall later
give it another name, but can base
all our discussions on this table.
Another Sample
Truth Table
|
A |
B |
C |
F2(A, B, C) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Two Truth
Tables in One
|
A |
B |
C |
F1(A, B, C) |
F2(A, B, C) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Truth tables are often used to
show pairs of functions, such as these two,
which will later be shown to be
related. This is easier than two
complete tables.
Truth tables rarely show more
than two functions, just because large truth
tables are “messy” and hard to
read.
Labeling
Rows in a Truth Table
The
row numbers are just labels. They are
not really a part of the truth table, but
aid in our discussions and
conversions to Boolean expressions.
The
row numbers are the decimal equivalents of the variable values viewed as binary
|
Row
Number |
X |
Y |
Z |
F(X,
Y, Z) |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
numbers.
The first row is always “row 0”.
0 = 0·4 + 0·2 + 0·1
1 = 0·4 + 0·2 + 1·1
2 = 0·4 + 1·2 + 0·1
3 = 0·4 + 1·2 + 1·1
4 = 1·4 + 0·2 + 0·1
5 = 1·4 + 0·2 + 1·1
6 = 1·4 + 1·2 + 0·1
7 = 1·4 + 1·2 + 1·1
The S and P Notations
These
can be viewed as shorthand notation for expressing truth tables.
S notation: Give
the row numbers in which the function has value 1.
P notation: Give
the row numbers in which the function has value 0.
Example: The
Exclusive OR (XOR) function
|
Row Number |
X |
Y |
X Å Y |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
0 |
X Å Y = S ( 1, 2 ) X Å Y = P ( 0, 3 )
Exercise: Convert
F(X, Y, Z) = S ( 0, 2, 4, 6 ) to the P notation.
Answer: The
function has three variables, so the truth table has 23 = 8 rows,
numbered 0 through
7. If rows 0, 2, 4, and 6 have ones,
then the rows
containing zeroes
must be 1, 3, 5, and 7. F(X, Y, Z) = P ( 1, 3, 5, 7 ).
Examples: F1
and F2
Consider
the two functions (F1 and F2), which we shall explain later.
|
Row |
A |
B |
C |
F1(A, B, C) |
F2(A, B, C) |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
|
3 |
0 |
1 |
1 |
0 |
1 |
|
4 |
1 |
0 |
0 |
1 |
0 |
|
5 |
1 |
0 |
1 |
0 |
1 |
|
6 |
1 |
1 |
0 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
1 |
F1(X, Y, Z) = S ( 1, 2, 4, 7 ) = P ( 0, 3, 5, 6 )
F2(X, Y, Z) = S ( 3, 5, 6, 7 ) = P ( 0, 1, 2, 4 )
Evaluation
of Boolean Expressions
The
relative precedence of the operators is:
1) NOT do this first
2) AND
3) OR do
this last
As
in the usual algebra, parentheses take precedence.
A·B + C·D, often written as AB + CD, is read as (A·B) + (C·D)
![]() is read as
is read as ![]() . The latter is really
messy.
. The latter is really
messy.
A·B + C·D = 1·0 + 1·1 = 0 + 1 = 1
A·(B + C)·D = 1·(0 + 1)·1 = 1 · 1 · 1 = 1
![]() =
= ![]() = 0 · 0 + 1 · 0 = 0 + 0 = 0
= 0 · 0 + 1 · 0 = 0 + 0 = 0
![]() =
= ![]() =
= ![]() = 1
= 1
![]() =
= ![]() = 0 · 1 = 0
= 0 · 1 = 0
The Basic
Unusual Boolean Theorem
Here
are two sets of theorems in Boolean algebra.
For all X 0·X = 0 OK
For all X 1·X = X OK
For all X 0 + X = X OK
For all X 1 + X = 1 What?
Consider
the following truth tables
|
W |
X |
W + X |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
From this, we derive the truth
table proving the last two theorems.
|
X |
0 + X |
1 + X |
|
0 |
0 |
1 |
|
1 |
1 |
1 |
The
Principle of Duality
If
a statement in Boolean algebra is true, so is its dual.
To
take the dual of an expression do the following:
change all logical AND to logical
OR and all logical OR to logical AND
change all 0 to 1 and 1 to 0.
Postulate Dual
0·X = 0 1
+ X = 1
1·X = X 0
+ X = X
0 + X = X 1·X = X
1 + X = 1 0·X = 0
An Unexpected Pair: Two
distributive laws, each the dual of the other.
For
all Boolean values of Boolean variables A, B, C: A·(B + C) = A·B + A·C
For
all Boolean values of Boolean variables A, B, C: A + B·C = (A + B)·(A + C)
If
A = 1, the statement becomes 1 + B·C = (1 + B)·(1 + C), or 1 = 1·1.
If
A = 0, the statement becomes 0 + B·C = (0 + B)·(0 + C), or B·C = B·C.