Implementation of Boolean Logic by Digital Circuits

We now consider the use of electronic circuits to implement Boolean functions
and arithmetic functions that can be derived from these Boolean functions.

Digital circuits are built from standard analog components, such as transistors.
It is the manner in which these transistors are used that causes them to display
the properties required for a digital circuit.

Early digital circuits were based on electromechanical relays, automatic
switches that were either “on” or “off”.

Relay On Relay Off

In 1937, George Stibitz of Bell Labs developed what he called the “Model K”.
It was a binary full adder based on relays implementing Boolean logic.
He developed the device at home in his kitchen; hence the name.

In 1938, Konrad Zuse developed a relay–based digital computer, the Z-1, in
his parents’ apartment in Berlin. It was lost to bombing during the war.

Digital Technologies

There are quite a few ways to build digital circuits. The choice of which to use
in any given device is based on a tradeoff of cost, speed, and power usage.

This course is based on an older technology that is a bit simpler to understand.
This technology is still seen in digital labs used for teaching.

The technology is called TTL (Transistor–Transistor Logic). It is based on the
use of transistors in a mode in which they act as switches, much like relays.

Logically, each TTL device is a Boolean device. All inputs to this device and
outputs from this device are either logic 0 or logic 1.

Electrically, these TTL devices are built to a standard that determines how
voltages into the device will be interpreted and what voltage is output.

Here are the voltage standards for active high TTL, the variety we study.

Input to Device Output by Device

Logic 1 2.0 to 5.0 volts 2.4 to 5.0 volts

Logic 0 0.0 to 0.8 volts 0.0 to 0.4 volts

Note the greater latitude on input specifications to allow for voltage degradation.

Basic Digital Circuit Elements

We have already discussed these gates, but present them again.

NOT This function takes one input and produces one output. The gate is shown
below. The circle at the right end of the triangle is important.

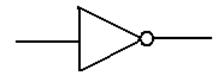
Algebraically, this function is denoted f(X) = X’ or f(X) =

The evaluation of the function is simple: = 1 and = 0.

Here is the truth table for the NOT operator.

X
0	1
1	0

Basic Boolean Operators (Part 2)

Logic OR

This is a function of two Boolean variables. We denote the logical OR of two Boolean
variables X and Y by “X + Y”. Some logic books will use “X Ú Y”.

The evaluation of the logical OR function is shown by a truth table

X	Y	X + Y
0	0	0
0	1	1
1	0	1
1	1	1

Basic Boolean Operators (Part 3)

Logic AND

This is a function of two Boolean variables. We denote the logical AND of two Boolean
variables X and Y by “X · Y”. Some logic books will use “X Ù Y”.

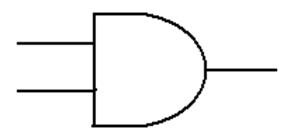
The evaluation of the logical AND function is shown by a truth table

X	Y	X · Y
0	0	0
0	1	0
1	0	0
1	1	1

Another Boolean Operator

While not a basic Boolean operator, the exclusive OR is very handy.

Logic XOR

This is a function of two Boolean variables. We denote the logical XOR of two Boolean
variables X and Y by “X Å Y”. Most logic books seem to ignore this function.

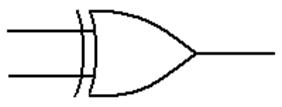
The evaluation of the logical XOR function is shown by a truth table

X	Y	X Å Y
0	0	0
0	1	1
1	0	1
1	1	0

From this last table, we see immediately that
X Å 0 = X and X Å 1 =

Other Logic Gates

The top gate shows the NOR gate and its logical equivalent.
The bottom line shows the NAND gate and its logical equivalent.

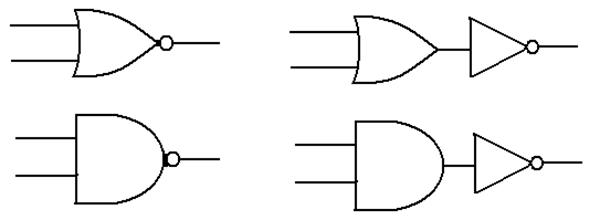
In my notes, I call these “derived gates” as they are composites of Boolean gates
that are more basic from the purely theoretical approach.

X Y OR NOR X Y AND NAND

0 0 0 1 0 0 0 1

0 1 1 0 0 1 0 1

1 0 1 0 1 0 0 1

1 1 1 0 1 1 1 0

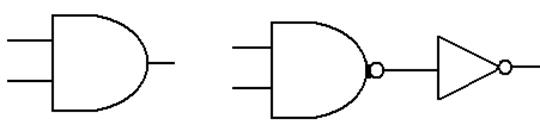
AND Gates and OR Gates: The Real Way

In actual fact, the NAND and NOR gates are more primitive than the AND, OR,
and NOT gates in that they are easier to build from transistors.

AND is NOT (NAND)

X Y NAND AND

0 0 1 0

0 1 1 0

1 0 1 0

1 1 0 1

OR is NOT (NOR)

X Y NOR OR

0 0 1 0

0 1 0 1

1 0 0 1

1 1 0 1

Implementation of Basic Circuits

These circuits use simple switches to implement NOT, NOR, and NAND gates.

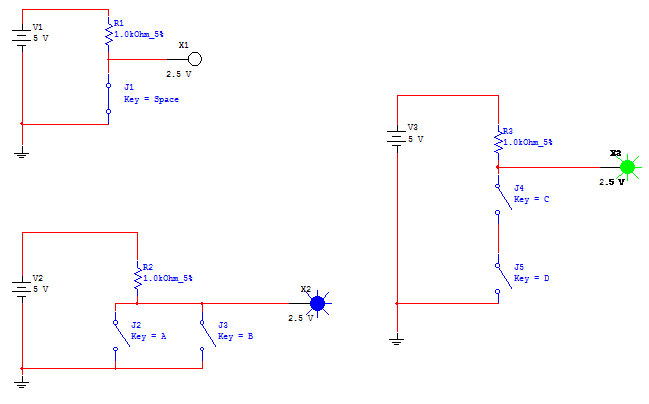
In the circuit at right, if both switches are closed, (logic 1), the output is 0 volts.
If neither or only one is closed, the output is 5 volts. This is a NAND gate.

The NOR Gate Implemented in CMOS

The NAND Gate Implemented in CMOS

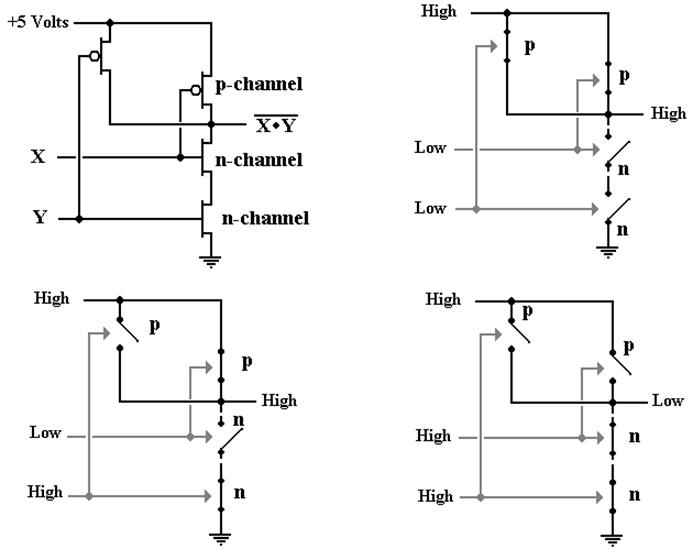
The OR Gate and the AND Gate

The NAND Gate as a Universal Gate

We show how to use a NAND gate to implement the three basic gates of
Boolean logic: AND, OR, and NOT.

We begin with a simple NAND gate and its truth table.

X	Y	X·Y
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

We now use the NAND gate to implement the basic Boolean devices.

The NAND Gate as a NOT Gate or an AND Gate

Note in the above truth table, that if Y = X, then = = .

Here is the NAND implementation of the NOT gate.

Since the NAND gate is logically equivalent to NOT (AND), we may use
“double negation” to say that the AND gate is equivalent to NOT (NAND).

Here is the AND gate as implemented from two NAND gates.

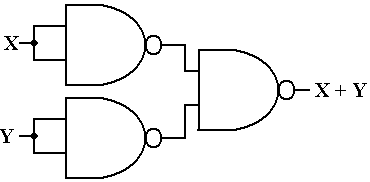
The NAND Gate as an OR Gate

In order to fabricate an OR gate from NAND gates, we must recall
DeMorgan’s laws.

One of DeMorgan’s laws is usually stated as = + .

This can be changed to the form = + = X + Y.

Here is the circuit.

Multiple–Input Gates

The standard definitions of the AND and OR gates call for two inputs.

3–input and 4–input varieties of these gates are quite common.
Here we give informal, but precise, definitions.

Gate Number of Inputs Output

NOT Exactly 1 0 if input is 1, 1 if input is 0

AND 2 or more 0 if any input is 0
1 if and only if all inputs are 1.

OR 2 or more 1 if any input is 1
0 if and only if all inputs are 0.

NAND 2 or more 1 if any input is 0
0 if and only if all inputs are 1

NOR 2 or more 0 if any input is 1
1 if and only if all inputs are 0.

Example: “Changing the Number of Inputs”

Some lab experiments call for gates with input counts other than what we have.

We begin with two ways to fabricate a 4–input AND gate from 2–input ANDs.

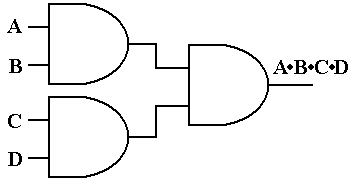
Another Example

We now consider how to take a 4–input AND gate and make it act
as if it were a 2–input AND gate.

There are always multiple solutions. Here are two solutions.
There are many others.

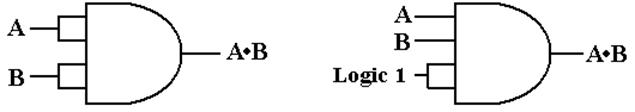
Fan–Out

By definition, the fan–out of a logic gate is the number of other logic
gates receiving input from it.

Considerations based on electrical engineering limit the fan–out of any gate.

Here is an OR gate with a fan–out of 5. It drives five other gates of some kind.

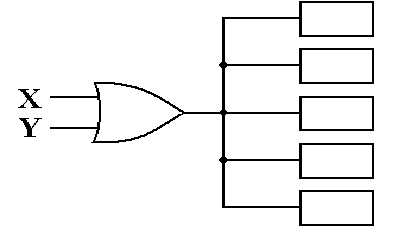
When the fan–out of a circuit element gets too large, there is a voltage sag.

This is similar to what can happen in a building when a large motor or
large electric heater turns on.

Controlling Fan–Out

Upon occasion, a given large circuit element will have a number of smaller
circuit elements fed from the same input.

There is a standard design trick to cause that big circuit to present
only one input to the “outside world”. Here is that trick.

Here the fan–out issue is transferred to the second NOT gate, which is
internal to the larger circuit element.