Example: Interpretation of a Digital Circuit

Here is a sample problem, taken from the textbook The Essentials of Computer Organization and Architecture by Linda Null and Julia Lobur.

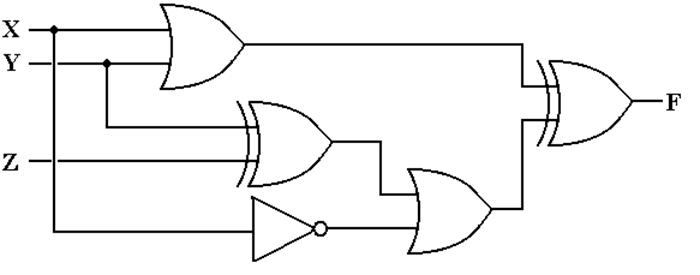
The task is to represent this circuit by both a Boolean expression and a
Truth Table. Admittedly, this will prove to be a silly circuit.

Interpreting a Digital Circuit: Step 1

Label the circuit elements (I have chosen to use numbers) and label the output
of each element. Note that we are slowly building a Boolean expression.

The outputs of each gate are as follows:
The output of gate 1 is (X + Y),
The output of gate 2 is (Y Å Z),
The output of gate 3 is X’,
The output of gate 4 is X’ + (Y Å Z), and
The output of gate 5 is (X + Y) Å [X’ + (Y Å Z)]

Interpreting a Digital Circuit: Step 2

For a circuit of this complexity, the best next step is to make a Truth Table.

X	Y	Z	X + Y	(Y Å Z)	X’	X’ + (Y Å Z)	(X + Y) Å [X’+(Y Å Z)]
0	0	0	0	0	1	1	1
0	0	1	0	1	1	1	1
0	1	0	1	1	1	1	0
0	1	1	1	0	1	1	0
1	0	0	1	0	0	0	1
1	0	1	1	1	0	1	0
1	1	0	1	1	0	1	0
1	1	1	1	0	0	0	1

We have now solved the problem. I want to continue and produce a simpler expression.
(At least I think that it is simpler).

Interpreting a Digital Circuit: Step 3

Present the truth table without the intermediate expressions. Use the standard rules to convert the truth table to either Canonical SOP or Canonical POS.
We do both.

X	Y	Z	F(X, Y, Z)
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

SOP: F(X, Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X·Y’·Z’ + X·Y·Z
0 0 0 0 0 1 1 0 0 1 1 1

POS: F(X, Y, Z) = (X + Y’ + Z) · (X + Y’ + Z’) · (X’ + Y + Z’) · (X’ + Y’ + Z)
0 1 0 0 1 1 1 0 1 1 1 0

Interpreting a Digital Circuit: Step 4

SOP:

F(X, Y, Z) = X’·Y’·Z’ + X’·Y’·Z + X’·Y’·Z’ + X·Y’·Z’ + X·Y·Z
= X’·Y’·(Z’ + Z) + (X + X’)·Y’·Z’ + X·Y·Z
= X’·Y’ + Y’·Z’ + X·Y·Z

POS:

F(X, Y, Z) = (X + Y’ + Z) · (X + Y’ + Z’) · (X’ + Y + Z’)
· (X’ + Y’ + Z) · (X + Y’ + Z)
= (X + Y’) · (X’ + Y + Z’)· (Y’ + Z)

One can also write

F(X, Y, Z) = S(0, 1, 4, 7)

F(X, Y, Z) = P(2, 3, 5, 6)

This is about as simple as I can make these expressions.

Building a Digital Circuit for a Boolean Expression

We take as examples two representations of the same Boolean expression.

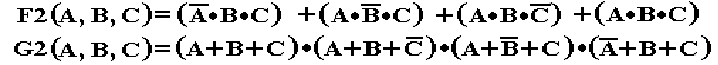
Sum of Products

SOP One OR gate connecting the output of a number of AND gates.

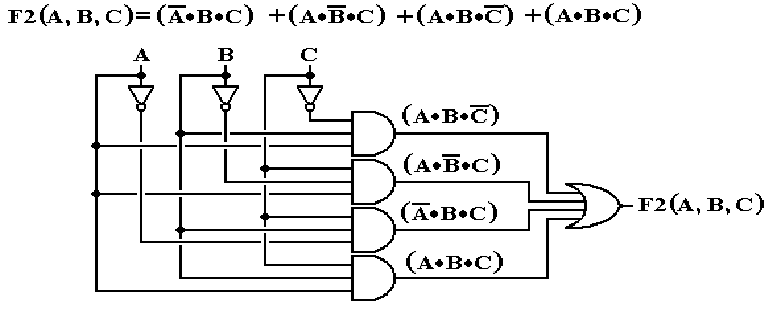
Building a Digital Circuit (Part 2)

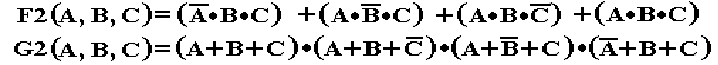
Product of Sums

POS One AND gate connecting the output of a number of OR gates.

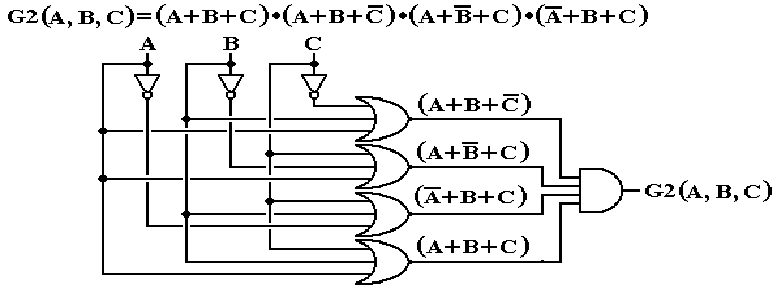
There are simpler Boolean expressions that are equivalent to both F2 and G2,
which are equivalent to each other. We study simplification later.

Stylistics

There are very few issues involved in drawing a digital implementation of
a Boolean circuit. The basic issue is DRAWING NEATLY.

My style of having the inputs at the top, with each input immediately feeding a NOT gate, if necessary, is only a convention. It helps me minimize the clutter in a drawing. The student may adopt any style that is easy to understand.

Big Gates

This style will ask for gates with a large number of inputs.
Here is an 8–input AND fabricated from three 4–input AND gates.

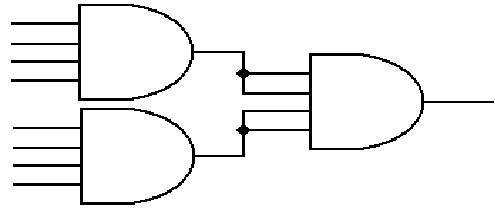
The AND gate on the right could also be a 2–input or 3–input gate.