The Non–Inverting Buffer

We now spend some time investigating useful circuit elements
that do not directly implement Boolean functions.

The first element is the non–inverting buffer.

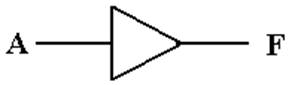
This is logically equivalent to two NOT gates in a row.

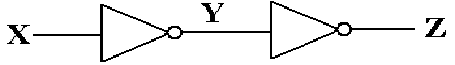
There are engineering differences between the two, most notably that the
non–inverting buffer delays the signal less than a chain of two NOT gates.

This is best considered a “voltage adjuster”.

A logic 1 (voltage in the range 2.0 – 5.0 volts) will be output as 5.0 volts.
A logic 0 (voltage in the range 0.0 – 0.8 volts) will be output as 0.0 volts.

Gate Delays

The output of a circuit element does not change instantaneously with the input, but only after a delay time during which the circuit processes the signal.

This delay interval, called “gate delay” is about 10 nanoseconds for most simple TTL circuits and about 25 nanoseconds for TTL Flip–Flops.

The simplest example is the NOT gate.

Here is a trace of the input and output. Note that the output does not reflect the input until one gate delay after the input changes.

For one gate delay time we have both X = 1 and Y = 1.

Delay Circuits

For some advanced designs, it is desirable to delay a signal by a fixed amount.

One simple circuit to achieve this effect is based on the Boolean identity.

A circuit to implement this delay might appear as follows.

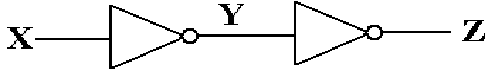
Here is the time trace of the input and output.

The Pulse Generator

This circuit represents one important application of the gate delay principle.
We shall present this circuit now and use it when we develop flip–flops.

This circuit, which I call a “pulse generator”, is based on the Boolean identity.

Here is the circuit

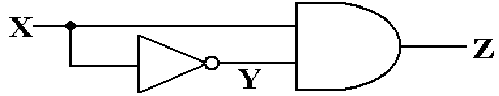
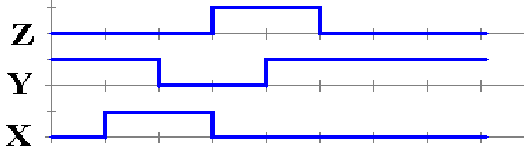
Here is a time plot of the circuit’s behavior.

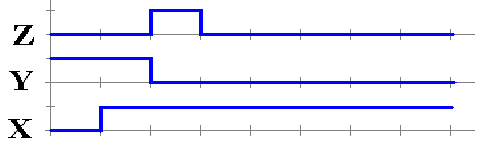
The pulse is due to the fact that for 1 gate delay, we have both X = 1 and Y = 1.
This is the time it takes the NOT gate to respond to its input and change Y.

The Tri–State Buffer

Some time ago, we considered relays as automatic switches.
The tri–state buffer is also an automatic switch.

Here are the diagrams for two of the four most popular tri–state buffers.

An enabled–low buffer is the same as an enabled–high buffer with a NOT gate.

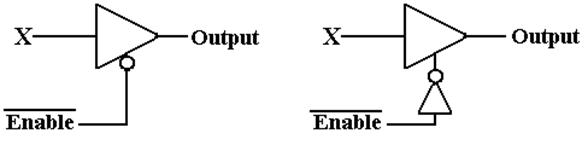
What does a tri–state buffer do when it is enabled?
What does a tri–state buffer do when it is not enabled?
What is this third state implied by the name “tri–state”?

An Enabled–High Tri–State Buffer

Consider an enabled–high tri–state buffer, with the enable signal called “C”.
When C = 1, the buffer is enabled.
When C = 0, the buffer is not enabled.

What does the buffer do?

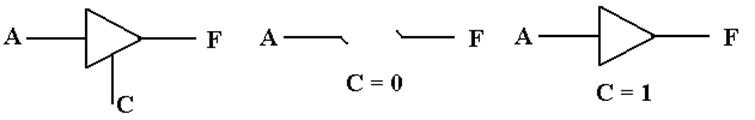
The buffer should be considered a switch. When C = 0, there is no connection between the input A and the output F. When C = 1, the output F is connected to the input A via what appears to be a non–inverting buffer.

Strictly speaking, when C = 0 the output F remains connected to input A, but through a circuit that offers very high resistance to the flow of electricity. For this reason, the state is often called “high impedance”, “impedance” being an engineer’s word for “resistance”.

What is This Third State?

Consider a light attached to a battery. We specify the battery as 5 volts,
due only to the fact that this course is focused on TTL circuitry.

0 volts to lamp Third state 5 volts to lamp

When the switch is closed and the lamp is connected to the battery, there
is a voltage of +5 volts on one side, 0 volts on the other, and the lamp is on.

In the case at left, both sides of the lamp are connected to 0 volts.
Obviously, it does nothing.

The middle diagram shows the third state. The top part of the lamp is not directly connected to either 0 volts or 5 volts.

In this third state, the lamp is not illuminated as there is no power to it.
This is similar to the state in which the top is set to 0 volts, but not the same.

Understanding Tri–State Buffers

The best way to understand a tri–state buffer is to consider this circuit.

When C = 0 The top buffer is outputting the value of A (logic 0 or logic 1)
The bottom tri–state buffer is not active.
F = A

When C = 1 The top tri–state buffer is not active.
The bottom buffer is outputting the value of B.
F = B

Due to the arrangement, exactly one tri–state buffer is active at any time.

We shall use tri–state buffers to attach circuit elements to a common bus,
and trust the control circuitry to activate at most one buffer at a time.