Standard Boolean Forms

In this section, we develop the idea of standard forms of Boolean expressions.
In part, these forms are based on some standard Boolean simplification rules.

Standard forms are either canonical forms or normal forms.

The standard expressions are in either

       SOP      Sum of Products form, or

       POS      Product of Sums form.

This lecture will focus on the following:

       Canonical Sum of Products

       Normal Sum of Products

       Canonical Product of Sums

       Normal Product of Sums

We shall also discuss a few more variants that have no standard names.

IMPORTANT:     These forms use only the 3 basic Boolean functions:
                           AND, OR, NOT.  Specifically, XOR is not used.

Variables and Literals

We start with the idea of a Boolean variable.  It is a simple variable that can
take one of only two values: 0 (False) or 1 (True).

Following standard digital design practice, we use the values 0 and 1.

Following standard teaching practice, we denote all Boolean variables by
       single letters; normally “A”, “B”, “C”, “D”, or “W”, “X”, “Y”, “Z”.

A literal is either a Boolean variable or its complement.

       Literals based on the variable X:     X and .

       Literals based on the variable Y:     Y and .

 

NOTE:   X and  represent the same variable,
              but they are not the same literal.

              X and  represent different variables.

Product and Sum Terms

A product term is the logical AND of one or more literals,
       with no variable represented more than once.

A sum term is the logical OR of one or more literals,
       with no variable represented more than once.

The following are all valid product terms over the two variables X and Y.

       ·            ·Y            X·             X·Y

Forms, such as X·X· and X··Y are not considered, as X·X = X and
X· = 0, so X·X· = X· and X··Y = 0·Y = 0.

The following are all valid sum terms over the two variables X and Y.

       X + Y           X +             + Y          +

Single literals

According to the strict definition, a single literal is either a sum term or
a product term, depending on the context.  This is necessary to avoid
having to give a number of special cases in the following definitions.

Sum of Products and Product of Sums

A SOP (Sum of Products) expression is the logical OR of product terms.

A POS (Product of Sums) expression is the logical AND of sum terms.

Sample SOP expressions

       F1(X, Y)             = X·Y + ·

       G1(X, Y)             = ·Y + X·

       H1(X, Y, Z)        = X + ·Z

       Note:     If we did not allow single literals to be product terms, we
                     would have trouble classifying H(X, Y, Z), which is clearly SOP.

Sample POS expressions

       F2(X, Y)             = (X+Y) · (+)

       G2(X, Y)             = (+Y) · (X+)

       H2(X, Y, Z)        = X·(+ Z)

       Note:     POS expressions almost always have parentheses to indicate the
                     correct evaluation.

More on Ambiguous Forms

What is the form of the expression F(X, Y) = X + Y

1.    SOP       It is the logical OR of two product terms.
                     Each product term is a single literal.

2.    POS       It is a single sum term (X + Y)

 

Both statements are true.  In general, questions such as this do not concern us.
If you are asked a question like this on a test, either answer will be accepted.

 

This ambiguity comes from the definitional necessity of mentioning “the
logical AND of one or more terms” and “the logical OR of one or more terms”.

With two equally good answers to an ambiguous form, pick the one you like.

Inclusion

A product term T1 is included in a product term T2
       if every literal in T1 is also in T2.

A sum term T1 is included in a sum term T2
       if every literal in T1 is also in T2.

Consider the following examples:

F(A, B, C) = A·B + A·C + A·B·C
              Each of A·B and A·C is included in A·B·C.

G(A, B, C) = (A + B)·(A + C)·(A + B + C)
              Each of (A + B) and (A + C) is included in (A + B + C).

There is no inclusion in the next expression

F(A, B, C) = A·B + A·C + ·B·C
              The literal A does no appear in the third term.

The inclusion rule is based on literals, not just variables.

More on Inclusion

Consider       F1(A, B, C) = A·B + A·C + A·B·C
and               F2(A, B, C) = A·B + A·C

We claim that the two are equal for every value of A, B, and C.

Let A = 0
              Clearly  F1(A, B, C) = 0
                           F2(A, B, C) = 0

Let A = 1
              Then      F1(A, B, C) = B + C + B·C
              and        F2(A, B, C) = B + C

Notice that we still have inclusion in F1, as each of B and C is included in B·C.
We prove these versions of F1(A, B, C) = F2(A, B, C) using a truth table.

B

C

B·C

B + C

B + C + B·C

0

0

0

0

0

0

1

0

1

1

1

0

0

1

1

1

1

1

1

1

Last Word on Inclusion

If a SOP or POS expression has included terms, it can be simplified.

F1(A, B, C) = A·B + A·C + A·B·C is identically equal to
F2(A, B, C) = A·B + A·C

G1(A, B, C) = (A + B)·(A + C)·(A + B + C) is identically equal to
G2(A, B, C) = (A + B)·(A + C)

 

The conclusion is that Boolean expressions with included terms are needlessly
complicated.  We can simplify them by the application of trivial rules.

 

Note that duplication is a form of inclusion.

The expression F3(A, B) = A·B + A·B has 2 terms, each included in the other.

Non–Standard Expressions

Not every useful Boolean expression is in a standard form.

F(X, Y) = X Ĺ Y is not a standard form, due to the exclusive OR.

G(X, Y) = X·Y + (X + Y)·(+Y) is not in a standard form.
              This has both a product term and a sum term.

The fact that G(X, Y) can easily be converted to a standard form
       does not make it already in a standard form.

Let’s convert this to SOP.  I usually have difficulty in conversion to POS,
       unless I am using a method I have yet to describe.

The term X·Y is already a product term, so we convert (X + Y)·(+Y) to SOP.

(X + Y)·(+Y)  = X·(+Y) + Y·(+Y)
                           = X· + X·Y + Y· + Y·Y
                           = 0 + X·Y+ ·Y + Y      = (X + )·Y + Y
                           = 1·Y + Y = Y

So G(X, Y) = X·Y + Y = Y                   G(X, Y) = Y.

     

More on Non–Standard  Forms

Look at the Boolean function G(X, Y) = X·Y + Y.  There are two ways to
look at this.  Try both ways.

Let G(X, Y) = X·Y + Y = X·Y + 1·Y = (X + 1) ·Y = 1 ·Y = Y

Do a truth table proof of the equality.

X

Y

X·Y

X·Y + Y

0

0

0

0

0

1

0

1

1

0

0

0

1

1

1

1

Note that the column marked X·Y matches the one marked X·Y + Y.  The two
functions are identical.  Also note that the term Y is included in the term X·Y,
so that, by inclusión, the term X·Y can be eliminated from the expression.

Normal and Canonical Forms

A Normal SOP expression is a Sum of Products expression
       with no included product terms.

A Normal POS expression is a Product of Sums expression
       with no included sum terms.

A Canonical SOP expression over a set of Boolean variables is
       a Normal SOP expression in which each product term contains
       a literal for each of the Boolean variables.

A Canonical POS expression over a set of Boolean variables is
       a Normal POS expression in which each sum term contains
       a literal for each of the Boolean variables.

Note:     A canonical expression on N Boolean variables is made up
              of terms, each of which has exactly N literals.

Note:     One can do digital design based on either normal or canonical forms.
              The choice usually depends on the technology used.

 

Equivalence of Canonical Forms and Truth Tables

We can directly translate between either of the canonical forms and
a truth table using a standard set of rules.

To produce the Sum of Products representation from a truth table,

   a) Generate a product term for each row where the value of the function is 1.
   b) The variable is complemented if its value in the row is 0, otherwise it is not.

To produce the Product of Sums representation from a truth table,
   a) Generate a sum term for each row where the value of the function is 0.
   b) The variable is complemented if its value in the row is 1, otherwise it is not.

Row

X

Y

X Ĺ Y

0

0

0

0

1

0

1

1

2

1

0

1

3

1

1

0

SOP:      Terms for rows 1 and 2.  Row 1: ·Y, Row 2: X· F = ·Y + X·

POS:      Terms for rows 0 and 3. Row 0: (X + Y), Row 3: ( + )
              F = (X + Y)·( + )

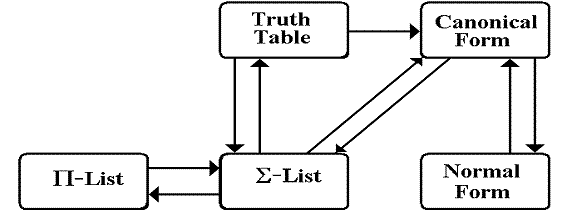
Examples: Conversions between the Three Forms

We have three equivalent ways to define a Boolean expression.

       1.    The Truth Table.

       2.    The S and P lists.

       3.    The Canonical Form.

In each of these depictions of the expression, we need to know the number
       of Boolean variables and labels to be assigned these variables.

It is easier to consider the SOP and POS cases separately, because the rules for
       conversion from the truth tables are so different for the two cases.

The figure below depicts the translations we shall consider for the SOP case.

Example Truth Table

Here is a truth table definition of a Boolean function of three Boolean variables.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

We shall discuss this function in both of its Sum of Product and
       Product of Sum representations.

We begin with SOP, the form that most students find easier.

 

SOP Example: Truth Table to S–List

Here is the truth table.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

Note that the function has value 1 in rows 3, 5, 6, and 7.

The function is F2(A, B, C) = S(3, 5, 6, 7).

 

SOP Example: S–List to Truth Table

The function is F2(A, B, C) = S(3, 5, 6, 7).

Create a truth table and place logic 1’s in rows 3, 5, 6, and 7.

Row

A

B

C

F2

0

0

0

0

 

1

0

0

1

 

2

0

1

0

 

3

0

1

1

1

4

1

0

0

 

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

Place 0’s in the other rows.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

SOP Example: Between S–List and P–List

Any function of N Boolean variables is represented by a truth table
       having 2N rows, numbered from 0 through (2N – 1).

The function is F2(A, B, C) = S(3, 5, 6, 7).

There will be 23 = 8 rows, numbered 0 through 7, in the truth table for F2.

To translate from one list form to the other list form, just pick the numbers
       in the range 0 … (2N – 1) that are not in the source list.

F2(A, B, C) = S(3, 5, 6, 7).  This is missing 0, 1, 2, and 4.  So,
F2(A, B, C) = P(0, 1, 2, 4)

The translation from the P–list to the S–list works in the same way.

 

SOP Example: Truth Table to Canonical Form

To produce the Sum of Products representation from a truth table,

   a) Generate a product term for each row where the value of the function is 1.
   b) The variable is complemented if its value in the row is 0, otherwise it is not.

Here again is the truth table.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

 

 

 

 

       The term is ·B·C

 

       The term is A··C

       The term is A·B·

       The term is A·B·C

F2(A, B, C) = ·B·C + A··C + A·B· + A·B·C

 

SOP Example: Between Canonical Form and S–List

Given F2(A, B, C) = ·B·C + A··C + A·B· + A·B·C

Write a 0 beneath each complemented variable and a 1 below each that is not.

Convert the N–bit numbers, assuming unsigned binary.

These are the rows of the truth table that have a 1.

F2(A, B, C) = ·B·C + A··C + A·B· + A·B·C
              0 1 1   1 0 1   1 1 0   1 1 1
                3       5       6       7

F2(A, B, C) = S(3, 5, 6, 7)

 

To convert the other way, just reverse the steps.

SOP Example: Between Canonical and Normal Forms

Given F2(A, B, C) = ·B·C + A··C + A·B· + A·B·C

To convert this to a simpler normal form, we must first make it more complex.

F2(A, B, C)  = ·B·C + A·B·C

                     + A··C + A·B·C

                     + A·B· + A·B·C

But        ·B·C + A·B·C = ( + A)·B·C = 1·B·C = B·C

              A··C + A·B·C = A·( + B)·C = A·1·C = A·C

              A·B· + A·B·C = A·B·( + C) = A·B·1 = A·B

So, F2(A, B, C)   = B·C + A·C + A·B

                           = A·B + A·C + B·C        The more standard notation.

 

POS Example: Truth Table to P–List

Here is the truth table.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

Note that the function has value 0 in rows 0, 1, 2, and 4.

The function is F2(A, B, C) = P(0, 1, 2, 4).

 

POS Example: P–List to Truth Table

The function is F2(A, B, C) = P(0, 1, 2, 4).

Create a truth table and place logic 0’s in rows 0, 1, 2, and 4.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

 

4

1

0

0

0

5

1

0

1

 

6

1

1

0

 

7

1

1

1

 

Place 1’s in the other rows.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

POS Example: Truth Table to Canonical Form

To produce the Product of Sums representation from a truth table,

   a) Generate a product term for each row where the value of the function is 0.
   b) The variable is complemented if its value in the row is 1, otherwise it is not.

Here again is the truth table.

Row

A

B

C

F2

0

0

0

0

0

1

0

0

1

0

2

0

1

0

0

3

0

1

1

1

4

1

0

0

0

5

1

0

1

1

6

1

1

0

1

7

1

1

1

1

 

       The term is (A + B + C)

       The term is (A + B + )

       The term is (A +  + C)

 

       The term is ( + B + C)

 

 

 

F2(A, B, C) = (A + B + C)·(A + B + )·(A +  + C)·( + B + C)

POS Example: Between Canonical Form and P–List

F2(A, B, C) = (A + B + C)·(A + B + )·(A +  + C)·( + B + C)

Write a 1 beneath each complemented variable and a 0 below each that is not.

Convert the N–bit numbers, assuming unsigned binary.

F2(A, B, C) = (A + B + C)·(A + B + )·(A +  + C)·( + B + C)
               0   0   0   0   0   1   0    1   0   1    0   0
                   0           1            2            4

F2(A, B, C) = P(0, 1, 2, 4)

 

To convert the other way, just reverse the steps.

POS Example: Between Canonical and Normal Forms

F2(A, B, C) = (A + B + C)·(A + B + )·(A +  + C)·( + B + C)

To convert this to a simpler normal form, we must first make it more complex.

F2(A, B, C)  = (A + B + C)·(A + B + )

                     ·(A + B + C)·(A +  + C)

                     ·(A + B + C)·( + B + C)

 

But        (A + B + C)·(A + B + ) = (A + B)

              (A + B + C)·(A +  + C) = (A + C)

              (A + B + C)·( + B + C) = (B + C)

So, F2(A, B, C)   = (A + B)·(A + C)·(B + C)