Logical Adjacency

K–Maps are a standard method for simplification of Boolean expressions.

The difference between K–Maps and Quine–McCluskey (Q–M) is that
K–M is well suited to manual solutions of small problems, and
Q–M lends itself to automated solutions.

Logical adjacency is the basis for all Boolean simplification methods.

The K–Map approach is a manual procedure that transforms logical adjacency
into physical adjacency on the paper. Simplification is done by inspection.

The key idea behind logical adjacency is expressed in the following
simplifications of Boolean expressions.

X·Y + X· = X·(Y + ) = X·1 = X

(X + Y)·(X + ) = X·X + X· + Y·X +Y·

= X·X + X· + X·Y + 0

= X·X + X· + X·Y

= X + X·( + Y) = X·1 = X + X = X

Logical Adjacency (Part 2)

Two Boolean terms are said to be logically adjacent when they contain the
same variables and differ in the form of exactly one variable.

Put another way, only one literal is different; a variable appears negated in one term
and is not negated in the other term. All other variables appear in the same way.

Consider the following lists of terms.

List 1 X

List 2 X·Y X· · ·Y

List 3 (X + Y) (X + ) ( + ) ( + Y)

In each of the lists, each term is logically adjacent not only to the term before it
but also to the term following.

In particular X·Y is adjacent to both X· and ·Y

(X + Y) is adjacent to both (X + ) and ( + Y).

In other words, the adjacency list is “circular”; the first item follows the last one.

Logical Adjacency (Part 3)

Here is the “circle” for SOP terms.

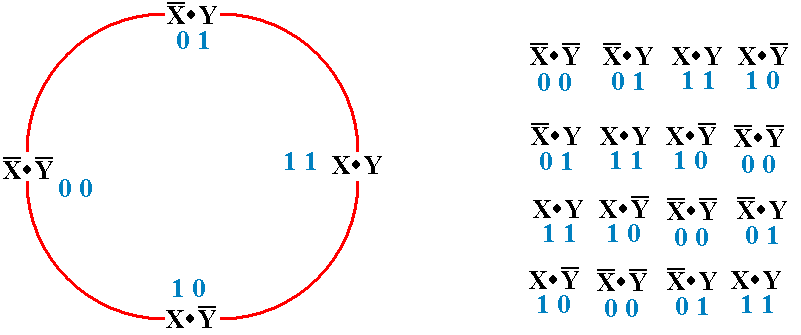
To produce a valid ordering, start at any part of the circle and read either clockwise
or counter–clockwise. Four valid orderings are shown at the right.

K–Maps for Small Variable Count: 2, 3, and 4

Some textbooks show K–Maps for 5 and 6 variables.

These are so complex as to be useless for manual computation. In those
cases the Quine–McCluskey method is used.

K–maps are shown as rectangles. Here are K–maps for 2, 3, and 4 variables.

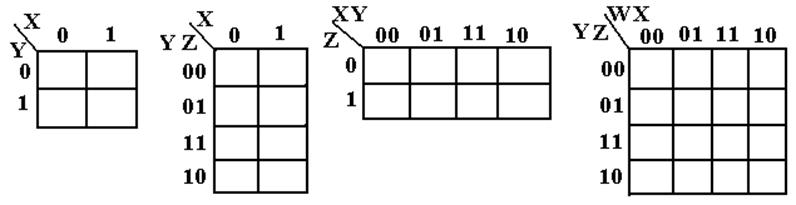
Note the structure of the list in cases where either a row or column corresponds
to two variables: 00, 01, 11, 10.

These are in the form of a Gray code, in which each term differs in exactly one bit
from the term preceding it and following it.

The Gray code structure causes logical adjacency to be seen as physical adjacency.

The “Complete” K–Map and Its Common Forms

Every entry in a K–map is either a 0 or a 1. These are the two values that
a Boolean function can assume.

While a “Complete” K–map has all entries filled, all common forms have only a
subset filled. Either the 1’s are placed and the 0’s omitted, or vice–versa.

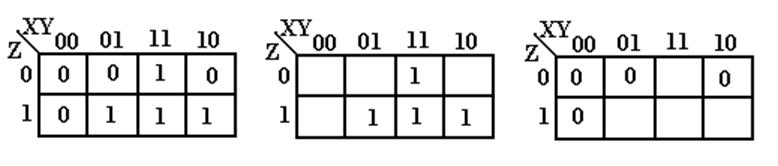
The three K–maps shown above contain identical information.

The second K–map shows the entries with values equal to 1.
Those entries not shown have value 0.

The third K–map shows the entries with values equal to 0.
Those entries not shown have value 1.

Creating a K–Map

The standard K–map is used to simplify Boolean expressions in canonical form;
each term has exactly one literal for every Boolean variable.

The method can be expanded to Boolean expressions not in canonical form.

SOP Expressions

Place a “1” in the K–Map for every term in the expression. The positions not
filled with a “1” are assumed to have a “0”.

POS Expressions

Place a “0” in the K–Map for every term in the expression. The positions not
filled with a “0” are assumed to have a “1”.

POS K–Map SOP K–Map

Locating Terms for Sum of Product Expressions

In SOP, each term is to be represented by a “1” in the K–map.

Where should that term be put?

Apply the “SOP Copy Rule” to each of the terms.

1. Write the variables in a standard uniform order.

2. Replace each complemented variable with a 0
Replace each plain variable with a 1.

Consider F(X, Y, Z) the term ·· corresponds to 0 0 0

the term ·Y·Z corresponds to 0 1 1

the term X··Z corresponds to 1 0 1

the term X·Y· corresponds to 1 1 0

the term X·Y·Z corresponds to 1 1 1

Locating the SOP Terms (Part 2)

Let us examine the SOP expression
F(X, Y, Z) = ·Y·Z + X··Z + X·Y· + X·Y·Z

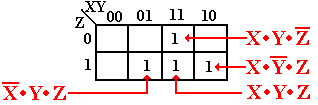
We place four “1”, one for each of the terms.

For ·Y·Z, the “1” is placed at X = 0, Y = 1, Z = 1.

For X··Z, the “1” is placed at X = 1, Y = 0, Z = 1.

For X·Y·, the “1” is placed at X = 1, Y = 1, Z = 0.

For X·Y·Z, the “1” is placed at X = 1, Y = 1, Z = 1.

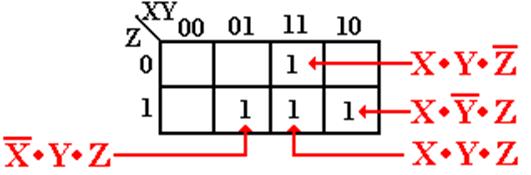
Combining the SOP Terms

Terms are combined into rectangles containing 2, 4, 8, or 16 squares.

Valid combinations: 2 by 1, 1 by 2
4 by 1, 2 by 2, 1 by 4
8 by 1, 4 by 2, 2 by 4, 1 by 8, etc.

Terms can be combined if the squares are adjacent either vertically or horizontally.

Any term can be a part of more than one combination.

The terms ·Y·Z and X·Y·Z, represented as 011 and 111, combine to –11, or Y·Z

The terms X··Z and X·Y·Z, represented as 101 and 111, combine to 1–1, or X·Z

The terms X·Y· and X·Y·Z, represented as 110 and 111, combine to 11–, or X·Y

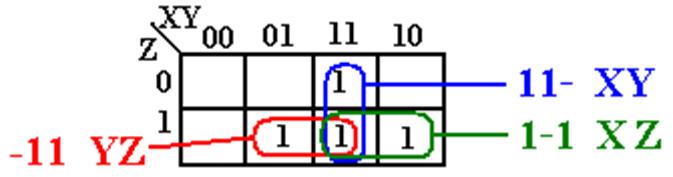
F(X, Y, Z) = X·Y + X·Z + Y·Z. Note 111 is used three times.

Adjacency and Logical Inclusion

Take another look at the above K–Map, with two of the simplifications removed.

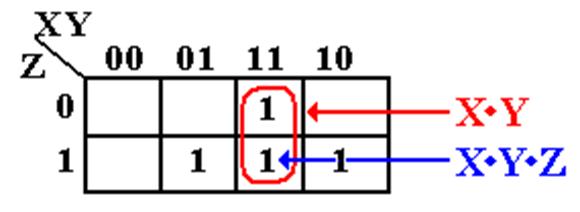
In terms of logical adjacency, the term X·Y covers the term X·Y·Z.

In terms of standard expressions, the term X·Y·Z includes the term X·Y.

In algebraic terms, the term X·Y stands for the sum term X·Y· + X·Y·Z, so
that X·Y + X·Y·Z is the same as X·Y· + X·Y·Z + X·Y·Z, which is obviously
the same as X·Y· + X·Y·Z. The last is equivalent to X·Y.

Simplification Using Algebra Alone

The straight algebraic simplification illustrates the K–Map approach.
It uses two basic Boolean identities: for any X, X + X = X.
for any X, + X = 1.

Given F(X, Y, Z) = ·Y·Z + X··Z + X·Y· + X·Y·Z

This is F(X, Y, Z) = ·Y·Z + X·Y·Z

+ X··Z + X·Y·Z

+ X·Y· + X·Y·Z

This is F(X, Y, Z) = ( + X)·Y·Z

+ X·( + Y)·Z

+ X·Y·( + Z)

This is F(X, Y, Z) = Y·Z + X·Z + X·Y,

or F(X, Y, Z) = X·Y + X·Z + Y·Z.

Locating Terms for Product of Sums Expressions

In POS, each term is to be represented by a “0” in the K–map.

Where should that term be put?

Apply the “POS Copy Rule” to each of the terms.

1. Write the variables in a standard uniform order.

2. Replace each complemented variable with a 1
Replace each plain variable with a 0.

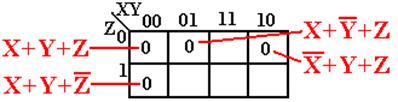
Consider F(X, Y, Z) the term X+Y+Z corresponds to 0 0 0

the term X + Y + corresponds to 0 0 1

the term X + + Z corresponds to 0 1 0

the term + Y + Z corresponds to 1 0 0

the term ++ corresponds to 1 1 1

Locating the POS Terms (Part 2)

Let us examine the POS expression
F(X, Y, Z) = (X + Y + Z)·(X + Y + )·(X + + Z)·( + Y + Z)

We place four “1”, one for each of the terms.

For (X + Y + Z), the “0” is placed at X = 0, Y = 0, Z = 0.

For (X + Y + ), the “0” is placed at X = 0, Y = 0, Z = 1.

For (X + + Z), the “0” is placed at X = 0, Y = 1, Z = 0.

For ( + Y + Z), the “0” is placed at X = 1, Y = 0, Z = 0.

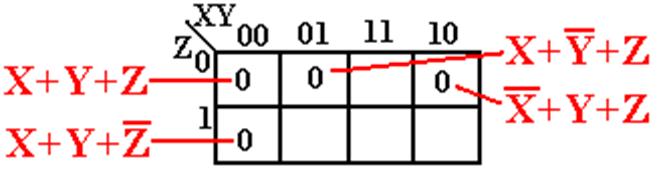
Example K–Map on 3 Variables

Consider the K–map shown above. It can be shown to represent the Boolean
expression F(X, Y, Z) = (X + Y + Z)·(X + + Z)·( + Y + Z)·(X + Y + ).

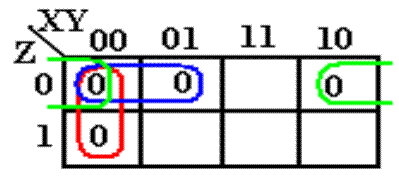
This is a K–map representation of a POS (Product of Sums) expression, also
called an expression in Conjunctive Normal Form.

The K–map procedure works by grouping adjacent squares. Here are the adjacencies:

000 and 010 group to form 0–0 representing the term (X + Z)

100 and 000 group to form –00 representing the term (Y + Z)

000 and 001 group to form 00– representing the term (X + Y)

The expression is F(X, Y, Z) = (X + Y)·(X + Z)·(Y + Z)

Handling Non–Canonical Terms

Suppose we have F(X, Y, Z) = (X + Y) (X + + Z)( + Y + Z)
How do we handle this?

For (X + + Z), denoted as 010, the “0” is placed at X = 0, Y = 1, Z = 0.

For ( + Y + Z), denoted as 100, the “0” is placed at X = 1, Y = 0, Z = 0.

But what about (X + Y), which is denoted as 00–?

The answer is to view the term as equivalent to the two terms

(X + Y + Z), denoted as 000

and (X + Y + ), denoted as 001.

For the term (X + Y) we would fill boxes 000 and 001 each with a “0”.

Another Simplification for SOP

Consider the Boolean Expression F(X, Y, Z) = S(3, 5, 6, 7).

The use of a K–Map to simplify this is simple.

First replace the decimal numbers by binary.

We have S(011, 101, 110, 111). Each of the numbers marks a cell in the K–Map.

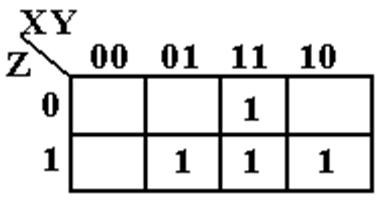
We have seen and solved this before, so we move on.

Still Another Try for SOP

Here is another function to consider. F(X, Y, Z) = S(1, 2, 4, 7).

This can be written as S(001, 010, 100, 111).

Here is the K–Map.

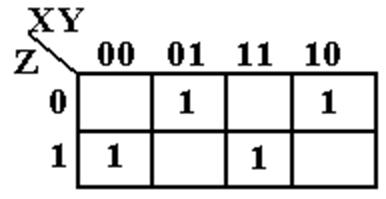
There are no logical adjacencies. The function cannot be simplified.

A K–Map for CNF Satisfiability

Consider the Boolean expression B₃ = ( + X)·W·( + )·(Y + Z).
Is this satisfiable? Here is the K–Map generated for this expression.

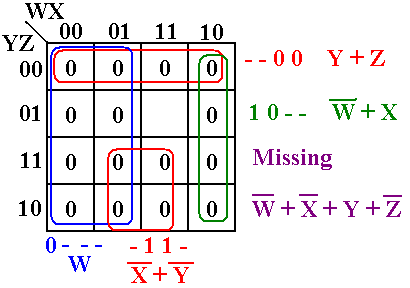
Note that there is one square in the K–map that is not covered by these expressions.
This corresponds to the term ( + +Y + ). The assignments that make this
missing term equal 0 are W = 1, X = 1, Y = 0, and Z = 1.

For these values, B₃ = ( + 1)·1·( + )·(0 + 1) = 1.
= (0 + 1)·1·(0 + 1)·(0 + 1) = 1. B₃ is satisfiable.

An Obvious Comment on the Above

Consider again the expression B₃ = ( + X)·W·( + )·(Y + Z).

It should be obvious that if W = 0, then B₃ = 0.

The only way to get B₃ = 1 demands the assignment W = 1.

Assuming W = 1, we have B₃ = ( + X)·1·( + )·(Y + Z)

= (0 + X)·1·( + )·(Y + Z)

= X·1·( + )·(Y + Z)

= X·( + )·(Y + Z)

= (X· + X·)·(Y + Z)

= (0 + X·)·(Y + Z)

= X··(Y + Z)

= X··Y + X··Z

= X·0 + X··Z

= X··Z

We now have W = 1, X = 1, Y = 0, and Z = 1.

Another K–Map for SAT

Consider the Boolean expression
B₄ = ( + )·( + Y)·(W + )·(W + Y)··

Here is the K–Map generated for this expression.

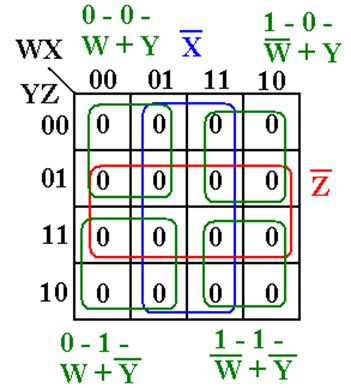
As a K–Map, this simplifies to B₄(W, X, Y, Z) = 0; it is not satisfiable.

More Comments on the Second Example

Note again the expression B₄ = ( + )·( + Y)·(W + )·(W + Y)··.

This can be true only if X = 0 and Z = 0.

Assuming that X = 0 and Z = 0, we have B₄ = ( + )·( + Y)·(W + )·(W + Y).

This is a Canonical POS expression on the two variables W and Y.

It has 4 = 2² terms; it cannot be satisfiable.

(In general terms, it has 2^N terms for N variables.)

Here is my version of the result on Circuit Satisfiability

Lemma: Let B be a CNF Boolean expression over N Boolean variables.
B is satisfiable if and only if it cannot be minimized
by any valid simplification method to B = 0 identically.