Encoders and Decoders:

Details and Design Issues

Edward L. Bosworth, Ph.D.

TSYS School of Computer Science

Columbus State University

Columbus, GA 31907

bosworth_edward@colstate.edu

Review of Binary Codes

We now begin a discussion of MSI (Medium Scale Integration) circuits.

MSI chips have complete circuits, built from multiple gates, on a single chip.

Two classes that we study are:

Encoders and Decoders

Multiplexers and Demultiplexers

These devices are based on binary coded input. We review simple binary codes.

2–bit codes: 00 0 3–bit codes: 000 0
01 1 001 1
10 2 010 2
11 3 011 3
100 4
101 5
110 6
111 7

Encoders

Encoders typically have 2^N inputs and N outputs.

These are called 2^N–to–N encoders.

Typical examples include 4–to–2 encoders (probably not used much)

8–to–3 encoders

16–to–4 encoders

Due to the prevalence of decimal arithmetic, we also have 10–to–4 encoders.

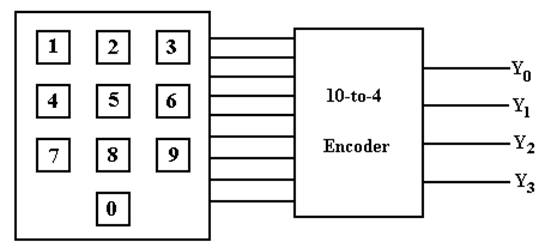
NOTE: We cannot encode 10 items with 3 bits; we need 4 bits to do this.

The Truth Table for a 10–to–4 Encoder

Input	Y3	Y2	Y1	Y0
X0	0	0	0	0
X1	0	0	0	1
X2	0	0	1	0
X3	0	0	1	1
X4	0	1	0	0
X5	0	1	0	1
X6	0	1	1	0
X7	0	1	1	1
X8	1	0	0	0
X9	1	0	0	1

In the table, we label the inputs X0 through X9, inclusive.
To produce the equations for the outputs, we reason as follows.

Y3 is 1 when either X8 = 1 or X9 = 1.

Y2 is 1 when X4 = 1 or X5 = 1 or X6 = 1 or X7 = 1.

Y1 is 1 when X2 = 1, X3 = 1, X6 = 1, or X7 = 1.

Y0 is 1 when X1 = 1, X3 = 1, X5 = 1, X7 = 1,
or X9 = 1.

These observations lead to the following equations, used to design the encoder.

Y3 = X8 + X9
Y2 = X4 + X5 + X6 + X7
Y1 = X2 + X3 + X6 + X7
Y0 = X1 + X3 + X5 + X7 + X9

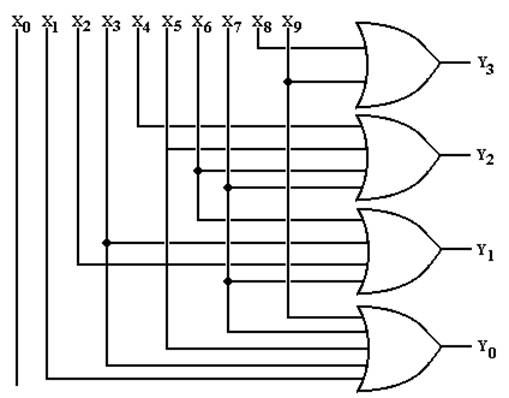
The Circuit Diagram for the 10–4 Encoder

The equations: Y3 = X8 + X9
Y2 = X4 + X5 + X6 + X7
Y1 = X2 + X3 + X6 + X7
Y0 = X1 + X3 + X5 + X7 + X9

The diagram:

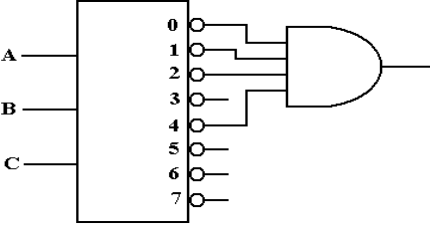
Issues with Encoders

In the above encoder, one should note that the input X₀ is not connected
to any output. An output of 0000 always implies that button 0 is pushed.

Put another way, this circuit does not distinguish between:

1. No input button pushed

2. Button 0 pushed.

If we really needed an indicator that a button had been pushed, we would have
a number of valid options. What we do is ignore the problem.

Decoders

Decoders are the opposite of encoders; they are N–to–2^N devices.

Typical examples include 2–to–4 decoders

3–to–8 decoders

4–to–16 decoders

Due to the prevalence of decimal arithmetic, we also have 4–to–10 decoders.

These are specialized 4–to–16 decoders with six fewer pins.

N–to–2^N decoders have N inputs, labeled X₀, X₁, …., X_N–1

2^N outputs, similarly labeled Y₀, Y₁, etc.

optionally, an enable line.

Decoders come in two varieties: active high and active low.

We focus our lectures on active high decoders:
the selected output goes to logic 1
the outputs not selected stay at logic 0.

Description of a 3–to–8 Decoder

This decoder has three inputs: X₂, X₁, X₀
eight outputs: Y₀, Y₁, Y₂, Y₃, Y₄, Y₅, Y₆, Y₇

Its functioning is best described by a modified truth table.

X2	X1	X0	Action
0	0	0	Y0 = 1, all others are 0
0	0	1	Y1 = 1, all others are 0
0	1	0	Y2 = 1, all others are 0
0	1	1	Y3 = 1, all others are 0
1	0	0	Y4 = 1, all others are 0
1	0	1	Y5 = 1, all others are 0
1	1	0	Y6 = 1, all others are 0
1	1	1	Y7 = 1, all others are 0

This gives rise to the equations:

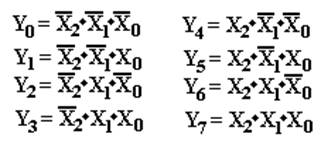
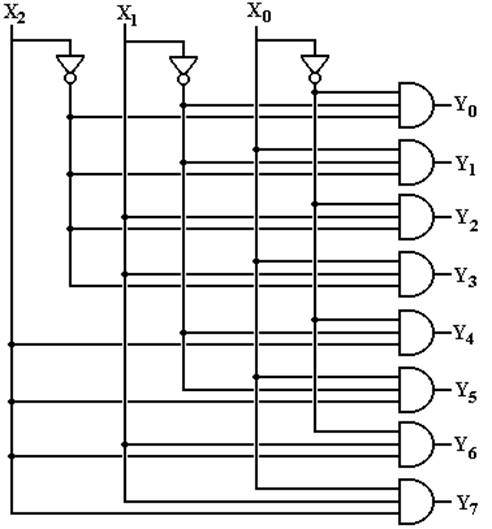
Circuit for a 3–to–8 Decoder

This follows from the equations.

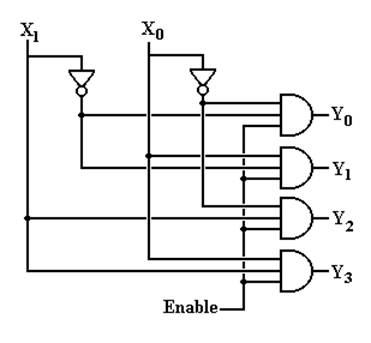
The Enable Input

Again, in the above circuit one output will always be active.

Suppose we want to have a decoder with no outputs active.

This is the function of the enable input, often denoted as “E”.

In an enabled high decoder, when E = 0 no output is active

when E = 1 the selected output is active

Here is the circuit diagram for a 2–to–4 decoder with enable input.

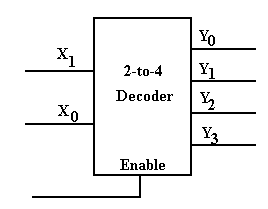
Decoders: Circuit Symbols and Truth Tables

We normally draw a decoder as a box, with inputs to the left and outputs to the
right. Note that the enable is drawn at the bottom.

The truth table for an active–high 2–to–4 decoder that is enabled high follows.

Enable	X1	X0	Y0	Y1	Y2	Y3
0	d	d	0	0	0	0
1	0	0	1	0	0	0
1	0	1	0	1	0	0
1	1	0	0	0	1	0
1	1	1	0	0	0	1

The “d” indicates that when Enable = 0, all outputs are 0 independent of X₀, X₁

What Do the Terms Mean?

Consider a two–to–four decoder, with two inputs (X₁ and X₀).

1. Which output becomes active for a given input pattern?
This is specified by the definition of a decoder.

2. Does the active output go to logic high or logic low?
For TTL, this is +5 volts or 0 volts.

3. How to manage the case in which no output should be active?

Active High vs. Active Low

Here are two decoders. One is active high and one is active low.
In each, output 2 has been selected.

In both circuits, we imagine each of the four outputs as attached to a LED,
which illuminates when it is fed with a logic 1.

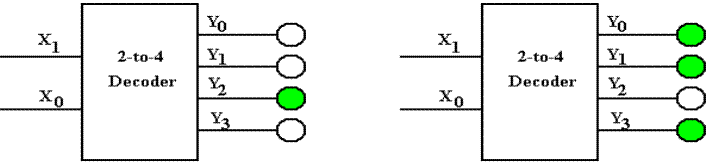
In the circuit at left, only the selected output illuminates its LED.
It is active high.

In the circuit at right, every output but the selected output illuminates its LED.
It is active low.

In many circuits, active low appears to be the preferred mode.

Active–Low, Enabled–Low Two–to–Four Decoder

Here is a truth table for this circuit.

Enable	X1	X0	Y0	Y1	Y2	Y3
1	d	d	1	1	1	1
0	0	0	0	1	1	1
0	0	1	1	0	1	1
0	1	0	1	1	0	1
0	1	1	1	1	1	0

If Enable = 1, all outputs are 1.

If Enable = 0, then the input (X₁X₀) selects the output that is enabled.

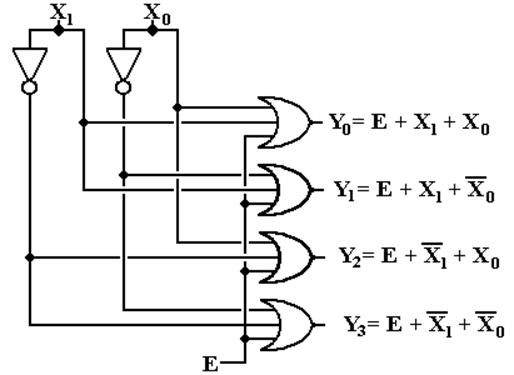
Here are the equations for the circuit. Here the enable is denoted by “E”.

Circuit for the Enabled–Low, Active–Low
Two–to–Four Decoder

Here it is. “E” denotes the enable input, but is not properly labeled
as “enable low”. I wanted the circuit to be a bit simple.

Where are the Decoders?

One will note that the Multi–Media Logic tool does not provide a decoder circuit.
Fortunately, a 1–to–2^N demultiplexer can be made into an N–to–2^N decoder.

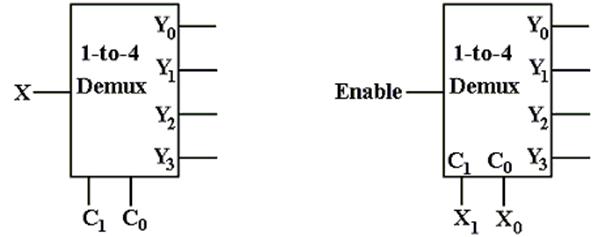
Look at the circuit to the left. The control signals C1,C0 select the output to receive
the input X. This is exactly equivalent to a decoder.

In the circuit at right, the selected output gets the input, now called “Enable”.
For the demultiplexers we use, the other outputs get a logic 1.

We can fabricate an active low decoder.

The MUX as an Active–Low Decoder

Here is the 2–to–4 Demultiplexer as an 2–to–4 active low decoder.

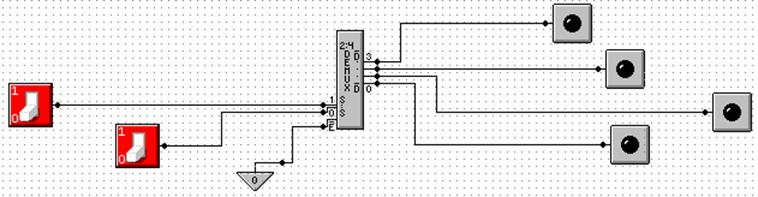
Here is an answer to one of the homework problems: use a 2–to–4 decoder for XOR.
The function is either S(1, 2) or P(0, 3).

Circuit Simulation Results

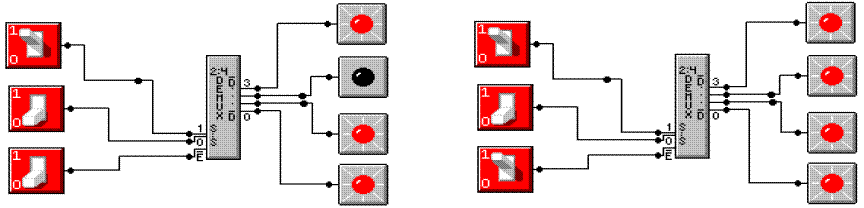
Enabled, Input 2 Not Enabled

Here we see a composite of two screen shots from Multimedia Logic.

At left, the decoder is enabled and input 2 is selected.
The selected output is logic 0.
All other outputs are logic 1.

At right, the decoder is not enabled. All outputs are logic 1.

Design with an N to 2^N Decoder

An N–to–2^N decoder has N inputs, 2^N outputs, and some control lines.

We can use such a decoder to implement any Boolean expression of N variables.

The two types of decoders are active high and active low.

Active–high decoders, connected to OR gates, are used to
implement Boolean expressions in SOP (Sum of Products) form.

Active–low decoders, connected to AND gates, are used to
implement Boolean expressions in POS (Product of Sums) form.
We do not discuss these.

Summary: 2 Boolean variables 2–to–4 decoder

3 Boolean variables 3–to–8 decoder

4 Boolean variables 4–to–16 decoder

5 Boolean variables 5–to–32 decoder

Implementation of SOP Expressions with Active High Decoders

These are the two functions that I have been using for quite some time.

With the decoder approach, it is best to design from the S–list expression.

If one has a truth table or canonical SOP expression, it is easier to first convert to the
S–list and then proceed with the design.

Here are F1 and F2. F1 = S(1, 2, 4, 7) and F2 = S(3, 5, 6, 7)

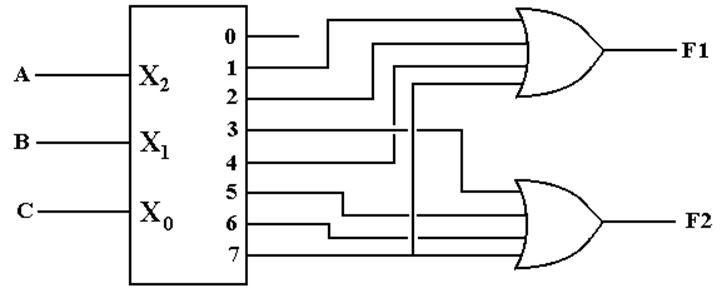
Just connect the numbered outputs into an OR gate and get the function.

Active Low Decoders

First, let’s use 3–to–8 decoders to describe the difference between
active high and active low.

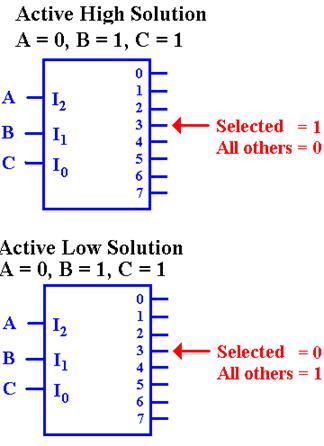
In the active–high decoder, the active output
is set to +5 volts (logic 1), while the other
outputs are set to 0 volts (logic 0).

In the active–low decoder, the active output
is set to 0 volts (logic 0), while the other
outputs are set to +5 volts (logic 1).

Enabled Low, Active Low Decoders

All commercial decoders have an enable input; most are enabled low.

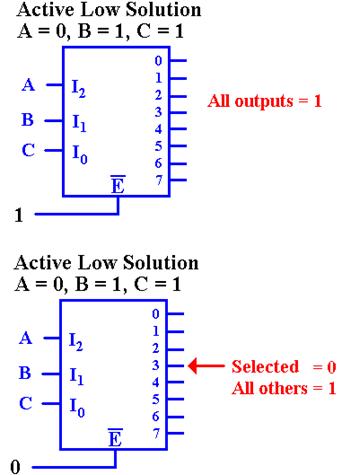
Since the decoder is enabled low, when the input
signal E’ = 1, none of the decoder outputs are active.
Since the decoder is active low, this means that all of
the outputs are set to logic 1 (+5 volts).

Since the decoder is enabled low, when the input signal E’ = 0,
the decoder is enabled and the selected output is active. Since
the decoder is active low, this means that the selected output is
set to logic 0, and all other outputs are set to logic 1.

Why Active Low / Enabled Low?

This is a conjecture, but it makes sense to me.

The active–high decoder is providing power to the device it enables.

The active–low decoder is just providing a path to ground for the device it enables.
It is likely that this approach yields a faster circuit.

Back To Active High: A Look At F2

Seeking a gate that outputs 1 if at least one of its inputs is 1, we are led to the OR gate.

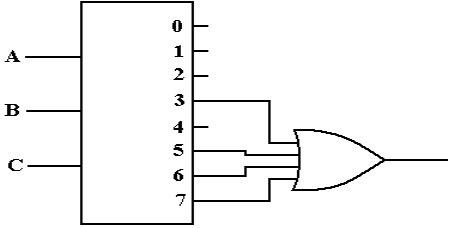
Active Low: F2(X, Y, Z) = P(0, 1, 2, 4)

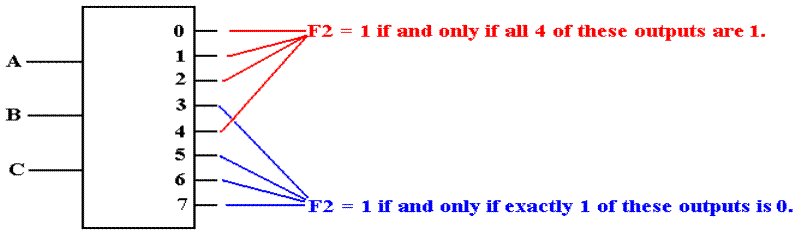
F2 is 1 if and only if none of the outputs Y₀, Y₁, Y₂, or Y₄ are selected. Specifically, each of
those outputs must be a logic 1. This leads to an AND gate implementation.