Modulo–4 Up–Down Counter

This is a counter with input.

If X = 0, the device counts up: 0, 1, 2, 3, 0, 1, 2, 3, etc.
If X = 1, the device counts down: 0, 3, 2, 1, 0, 3, 2, 1, etc.

Step 1a: Derive the state diagram and state table for the circuit.

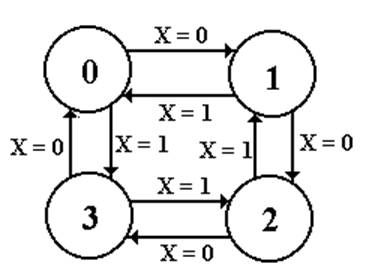
Note two transitions between the state pairs: one is up and one is down.

Step 1b: Derive the State Table

Present State	Next State
	X = 0	X = 1
0	1	3
1	2	0
2	3	1
3	0	2

This is just a restatement of the state diagram.

Note: Two columns for the “Next State”.

Step 2: Count the States and
Determine the Flip–Flop Count

Count the States

There are four states for any modulo–4 counter. N = 4

The states are simple: 0, 1, 2, and 3.

Calculate the Number of Flip–Flops Required

Let P be the number of flip–flops.

Solve 2^P-1 < N £ 2^P. So 2^P-1 < 4 £ 2^P and P = 2.

We need two flip–flops.

Step 3: Assign a unique P-bit binary number
(state vector) to each state.

Here P = 2, so we are assigning two–bit binary numbers.

Vector is denoted by the binary number Y₁Y₀.

State	2-bit Vector
	Y1 Y0
0	0 0
1	0 1
2	1 0
3	1 1

Each state has a unique 2–bit number assigned.

Any other assignment would be absurd.

Step 4: Derive the state transition table
and the output table.

There is no computed output, hence no output table.

The state transition table uses the 2–bit state vectors

Present State		Next State
		X = 0	X = 1
0	00	01	11
1	01	10	00
2	10	11	01
3	11	00	10

Step 5:Separate the state transition table into P tables,
one for each flip-flop.

Flip–Flop 1

Flip-Flop 1
PS	Next State: Y1
Y1Y0	X = 0	X = 1
0 0	0	1
0 1	1	0
1 0	1	0
1 1	0	1

Flip–Flop 0

Flip-Flop 0: Y0
PS	Next State
Y1Y0	X = 0	X = 1
0 0	1	1
0 1	0	0
1 0	1	1
1 1	0	0

Step 6: Decide on the types of flip-flops to use.
When in doubt, use all JK’s.

Here is the excitation table for a JK flip–flop

Q(T)	Q(T+1)	J	K
0	0	0	d
0	1	1	d
1	0	d	1
1	1	d	0

Step 7: Derive the input table for each flip-flop

Flip–Flop 1

	X = 0			X = 1
Y1Y0	Y1	J1	K1	Y1	J1	K1
0 0	0	0	d	1	1	d
0 1	1	1	d	0	0	d
1 0	1	d	0	0	d	1
1 1	0	d	1	1	d	0

Flip–Flop 0

	X = 0			X = 1
Y1Y0	Y0	J0	K0	Y1	J0	K0
0 0	1	1	d	1	1	d
0 1	0	d	1	0	d	1
1 0	1	1	d	1	1	d
1 1	0	d	1	0	d	1

Question: How do we produce equations for the J’s and K’s?

Step 8: Derive the input equations for each flip-flop

The equations are based on the present state and the input.

The input X produces a complication.

The simplest match procedure will lead to two equations
for each flip–flop input: one for X = 0 and one for X = 1.

Use the “combine rule”

The rule for combining expressions derived separately
for X = 0 and X = 1 is

·(expression for X= 0) + X·(expression for X = 1).

Rationale: Let F(X) = A· + B·X
When X = 0, F(X) = A and when X = 1, F(X) = B.

Input Equations for Flip–Flop 1

	X = 0			X = 1
Y1Y0	Y1	J1	K1	Y1	J1	K1
0 0	0	0	d	1	1	d
0 1	1	1	d	0	0	d
1 0	1	d	0	0	d	1
1 1	0	d	1	1	d	0

J₁ = Y₀ J₁ = Y₀’
K₁ = Y₀ K₁ = Y₀’

Apply the “combine rule”

J₁ = X’·Y₀ + X·Y₀’ = X Å Y₀

K₁ = X’·Y₀ + X·Y₀’ = X Å Y₀

Input Equations for Flip–Flop 0

	X = 0			X = 1
Y1Y0	Y0	J0	K0	Y1	J0	K0
0 0	1	1	d	1	1	d
0 1	0	d	1	0	d	1
1 0	1	1	d	1	1	d
1 1	0	d	1	0	d	1

J₀ = 1 J₀ = 1

K₀ = 1 K₀ = 1

Apply the “Combine Rule”

J₀ = X’·1 + X·1 = 1

K₀ = X’·1 + X·1 = 1

Neither J₀ nor K₀ depend on X. But Y₀ does not depend on X.

Step 9: Summarize the equations by
writing them in one place.

Here they are.

J₁ = X Å Y₀ K₁ = X Å Y₀
J₀ = 1 K₀ = 1

Step 10: Draw the Circuit

As designed, it is:

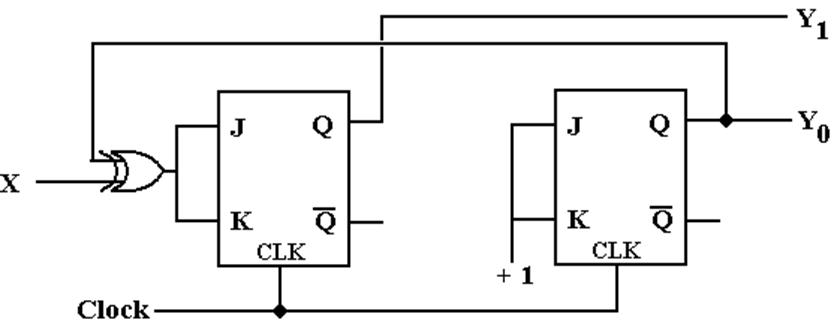
Step 10: Draw the Circuit

Implemented with T Flip–Flops, it is:

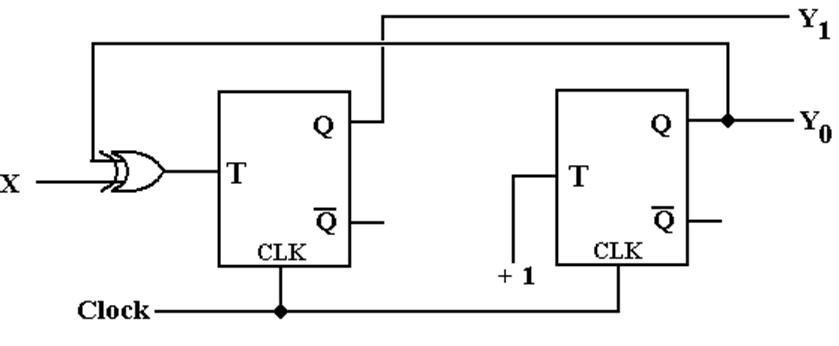
One could also use a 4–register “one hot” design, with the input X
used to determine the direction of the shift.