The Memory Component

The memory stores the instructions and data for an executing program.

Memory is characterized by the smallest addressable unit:
Byte addressable the smallest unit is an 8–bit byte.
Word addressable the smallest unit is a word, usually 16 or 32 bits in length.

Most modern computers are byte addressable, facilitating access to character data.

Logically, computer memory should be considered as an array.
The index into this array is called the address or “memory address”.

A logical view of such a byte addressable memory might be written in code as:

Const MemSize =
byte Memory[MemSize] // Indexed 0 … (MemSize – 1)

The CPU has two registers dedicated to handling memory.

The MAR (Memory Address Register) holds the address being accessed.

The MBR (Memory Buffer Register) holds the data being written to the
memory or being read from the memory. This is sometimes
called the Memory Data Register.

Primary Memory

Also called “core memory”, “store”, or “storage”.

Beginning with the MIT Whirlwind and continuing for about 30 years, the
basic technology for primary memory involved “cores” of magnetic material.

Requirements for a Memory Device

1. Random access by address, similar to use of an array. Byte addressable
memory can be considered as an array of bytes.
byte memory [N] // Address ranges from 0 to (N – 1)

2. Binary memory devices require two reliable stable states.

3. The transitions between the two stable states must occur quickly.

4. The transitions between the two stable states must not occur
spontaneously, but only in response to the proper control signals.

5. Each memory device must be physically small, so that a large number
may be placed on a single memory chip.

6. Each memory device must be relatively inexpensive to fabricate.

Varieties of Random Access Memory

There are two types of RAM

1. RAM read/write memory

2. ROM read–only memory.

The double use of the term “RAM” is just accepted. Would you say “RWM”?

Types of ROM

1. “Plain ROM” the contents of the memory are set at manufacture
and cannot be changed without destroying the chip.

2. PROM the contents of the chip are set by a special device
called a “PROM Programmer”. Once programmed
the contents are fixed.

3. EPROM same as a PROM, but that the contents can be erased
and reprogrammed by the PROM Programmer.

Memory Registers

MAR Memory Address Register
This specifies the address of the instruction or data item.

For a byte addressable memory, each byte has a distinct address.
For a word addressable memory, only the words have individual addresses.

MBR Memory Buffer Register
This holds the data read from memory or to be written to memory.
Occasionally called MDR for Memory Data Register

In a byte addressable memory, the MBR is usually 8 bits wide; that is, it
holds one byte.

In a 16–bit word addressable memory, the MBR would be 16 bits wide.

The size of the MBR is the size of an addressable item.

Memory Control Signals

Read / Write Memory must do three actions:

READ copy contents of an addressed word into the MBR

WRITE copy contents of the MBR into an addressed word

NOTHING the memory is expected to retain the contents written into
it until those contents have been rewritten.

One set of control signals Select – the memory unit is selected.
if 0 the CPU writes to memory, if 1 the CPU reads from memory.

Select		Action
0	0	Memory contents are not changed.
0	1	Memory contents are not changed.
1	0	CPU writes data to the memory.
1	1	CPU reads data from the memory.

A ROM has only one control signal: Select.

If Select = 1 for a ROM, the CPU reads data from the addressed memory slot.

Another Notation for Control Signals

There are several notations for control signals that are asserted low.
Consider the signal Select, which we have assumed to be asserted high.

Were this signal asserted low, it would be notated as either

The more modern notation uses a “#” after a signal name to
indicate that it is asserted low.

A similar notation is used with the “two option selector” control signals; e.g.,

Here, the “#” notation indicates what the signal indicates when it is low.

If R/W# = 0, a memory write is called for.
If R/W# = 1, a memory read is called for.

Memory Example with New Notation

Suppose that a memory is selected with an active low signal and
has another signal to indicate the operation.

The two tables below convey the same information.

		Action
1	0	Memory contents are not changed.
1	1	Memory contents are not changed.
0	0	CPU writes data to the memory.
0	1	CPU reads data from the memory.

Select#	R/W#	Action
1	0	Memory contents are not changed.
1	1	Memory contents are not changed.
0	0	CPU writes data to the memory.
0	1	CPU reads data from the memory.

Memory Timings

Memory Access Time

Defined in terms of reading from memory. It is the time between the address
becoming stable in the MAR and the data becoming available in the MBR.

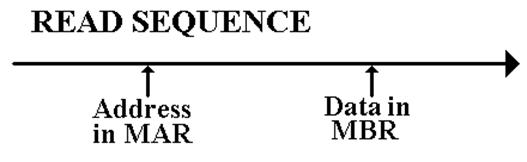
Memory Cycle Time

Less used, this is defined as the minimum time between two independent
memory accesses.

The Idea of an Address Space

The memory size is defined in terms of the amount of primary memory
actually installed.

The address space, determined by the size of the MAR, indicates the range
of addresses that actually can be generated.

Absent such kludges such as Expanded Memory and Extended Memory
(both obsolete, dating to about 1980), the memory size does not exceed
the size of the address space.

An N–bit MAR can address 2^N distinct memory locations, 0 … 2^N – 1

Computer	MAR bits	Address Range
PDP-11/20	16	0 to 65 535
Intel 8086	20	0 to 1 048 575
Intel Pentium	32	0 to 4 294 967 295

Memory Mapped Input / Output

Though not a memory issue, we now address the idea of memory mapped input
and output. In this scheme, we take part of the address space that would
otherwise be allocated to memory and allocate it to I/O devices.

The PDP–11 is a good example of a memory mapped device. It was a byte
addressable device, meaning that each byte had a unique address.

The old PDP–11/20 supported a 16–bit address space. This supported addresses
in the range 0 through 65,535 or 0 through 0177777 in octal.

Addresses 0 though 61,439 were reserved for physical memory.
In octal these addresses are given by 0 through 167,777.

Addresses 61,440 through 65,535 (octal 170,000 through 177,777) were
reserved for registers associated with Input/Output devices.

Examples: CR11 Card Reader 177,160 Control & Status Register
177,162 Data buffer 1
177,164 Data buffer 2

Reading from address 0177162 would access the card reader data buffer.

The Linear View of Memory

Memory may be viewed as a linear array, for example a byte–addressable memory

byte memory [N] ; // Addresses 0 .. (N – 1)

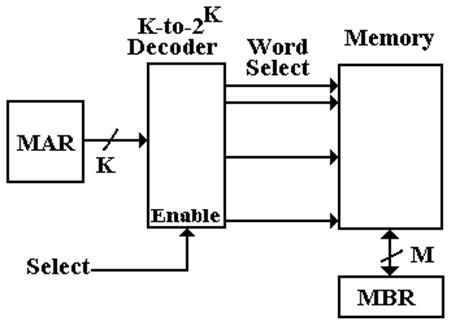
This is a perfectly good logical view, it just does not correspond to reality.

Memory Chip Organization

Consider a 4 Megabit memory chip, in which each bit is directly addressable.
Recall that 4M = 2²² = 2¹¹ · 2¹¹, and that 2¹¹ = 2, 048.

The linear view of memory, on the previous slide, calls for a 22–to–2²² decoder,
also called a 22–to–4,194,304 decoder. This is not feasible.

If we organize the memory as a two–dimensional grid of bits, then the design
calls for two 11–to–2048 decoders. This is still a stretch.

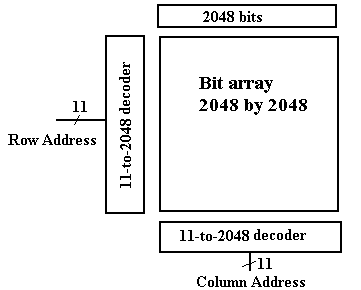
Managing Pin-Outs

Consider now the two–dimensional memory mentioned above. What pins are needed?

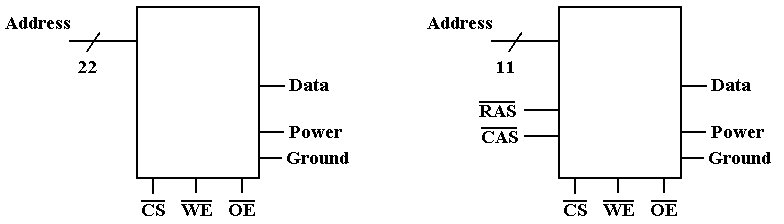
Pin Count
Address Lines 22 Address Lines 11
Row/Column 0 Row/Column 2
Power & Ground 2 Power & Ground 2
Data 1 Data 1
Control 3 Control 3
Total 28 Total 19

Separate row and column addresses require two cycles to specify the address.

Four–Megabyte Memory

Do we have a single four–megabyte chip or eight four–megabit memory chips?

One common solution is to have bit–oriented chips. This facilitates the
two–dimensional addressing discussed above.

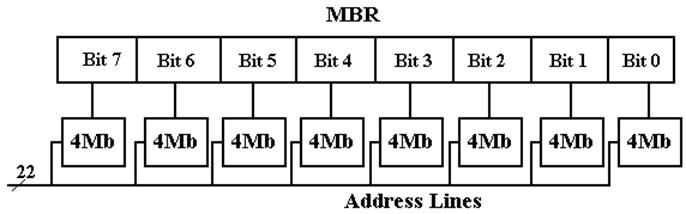
For applications in which data integrity is especially important, one might add a
ninth chip to hold the parity bit. This reflects the experience that faults, when
they occur, will be localized in one chip.

Parity provides a mechanism to detect, but not correct, single bit errors.

Correction of single bit errors requires twelve memory chips. This scheme will
also detect all two–bit errors.

Memory Interleaving

Suppose a 64MB memory made up of the 4Mb chips discussed above.
We now ignore parity memory, for convenience and also because it is rarely needed.

We organize the memory into 4MB banks, each having eight of the 4Mb chips.
The figure in the slide above shows such a bank.

The memory thus has 16 banks, each of 4MB.

16 = 2⁴ 4 bits to select the bank
4M = 2²² 22 bits address to each chip

Not surprisingly, 64M = 2²⁶.

Low–Order Interleaving

Bits	25 – 4	3 – 0
Use	Address to the chip	Bank Select

High–Order Interleaving (Memory Banking)

Bits	25 – 22	21 – 0
Use	Bank Select	Address to the chip

Faster Memory Chips

We can use the “2 dimensional” array approach, discussed earlier, to create a faster
memory. This is done by adding a SRAM (Static RAM) buffer onto the chip. Consider
the 4Mb (four megabit) chip discussed earlier, now with a 2Kb SRAM buffer.

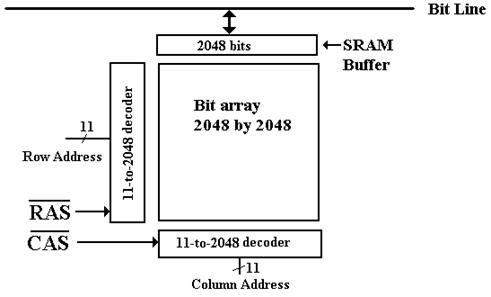
In a modern scenario for reading the chip, a Row Address is passed to the chip, followed
by a number of column addresses. When the row address is received, the entire row is
copied into the SRAM buffer. Subsequent column reads come from that buffer.

Memory Technologies: SRAM and DRAM

One major classification of computer memory is into two technologies

SRAM Static Random Access Memory

DRAM Dynamic Random Access Memory (and its variants)

SRAM is called static because it will keep its contents as long as it is powered.

DRAM is called dynamic because it tends to lose its contents, even when powered.
Special “refresh circuitry” must be provided.

Compared to DRAM, SRAM is
faster
more expensive
physically larger (fewer memory bits per square millimeter)

SDRAM is a Synchronous DRAM.
It is DRAM that is designed to work with a Synchronous Bus, one with a clock signal.

The memory bus clock is driven by the CPU system clock, but it is always slower.

SDRAM (Synchronous DRAM)

Synchronous Dynamic Random Access Memory

Suppose a 2 GHz system clock. It can easily generate the following memory bus clock
rates: 1GHz, 500 MHz, 250MHz, 125MHz, etc. Other rates are also possible.

Consider a 2 GHz CPU with 100 MHz SDRAM.
The CPU clock speed is 2 GHz = 2,000 MHz
The memory bus speed is 100 MHz.

In SDRAM, the memory transfers take place on a timing dictated by the memory
bus clock rate. This memory bus clock is always based on the system clock.

In “plain” SDRAM, the transfers all take place on the rising edge of the memory
bus clock. In DDR SDRAM (Double Data Rate Synchronous DRAM), the transfers
take place on both the rising and falling clock edges.

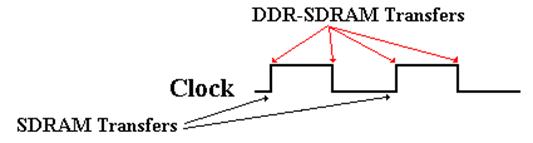
More on SDRAM

“Plain” SDRAM makes a transfer every cycle of the memory bus.
For a 100 MHz memory bus, we would have 100 million transfers per second.

DDR–SDRAM is Double Data Rate SDRAM

DDR–SDRAM makes two transfers for every cycle of the memory bus,
one on the rising edge of the clock cycle
one on the falling edge of the clock cycle.

For a 100 MHz memory bus, DDR–SDRAM would have 200 million transfers
per second.

To this, we add wide memory buses. A typical value is a 64–bit width.

A 64–bit wide memory bus transfers 64 bits at a time. That is 8 bytes at a time.

Thus our sample DDR–SDRAM bus would transfer 1,600 million bytes per second.

This might be called 1.6 GB / second, although it more properly is 1.49 GB / second,
as 1 GB = 1, 073, 741, 824 bytes.

Byte Addressing vs. Word Addressing

The addressing capacity of a computer is dictated by the number of bits in the MAR.

Suppose the MAR (Memory Address Register Contains) N bits.
Then 2^N items can be addressed.

In a byte addressable machine, the maximum memory size is 2^N bytes.

If the machine supports longword addressing, but not byte or word addressing,
the maximum memory size is 2^N+2 bytes.

Word and longword addressable machines might have their memory sized quoted in
bytes, but they do not access individual bytes.

Example: 256 KB PDP–11/70 vs. the CDC–6600 with 256 K words (60 bits each).

The CDC–6600 could have been considered to have 1,920 KB of memory. However,
it was not byte addressable; the smallest addressable unit was a 60–bit integer.

Almost every modern computer is byte addressable to allow direct access to the
individual bytes of a character string.

A modern computer that is byte addressable can still issue both word and longword
instructions. These just reference data two bytes at a time and four bytes at a time.

Word Addressing in a Byte Addressable Machine

Each 8–bit byte has a distinct address.

A 16-bit word at address Z contains bytes at addresses Z and Z + 1.

A 32-bit word at address Z contains bytes at addresses
Z, Z + 1, Z + 2, and Z + 3.

Note that computer architecture refers to addresses, rather than variables.

In a high–level programming language we use the term “variable” to indicate
the contents of a specific memory address.

Consider the statement Y = X

Go to the memory address associated with variable X

Get the contents

Copy the contents into the address associated with variable Y.

Big–Endian vs. Little–Endian Addressing

Address Big-Endian Little-Endian

Z 01 04

Z + 1 02 03

Z + 2 03 02

Z + 3 04 01

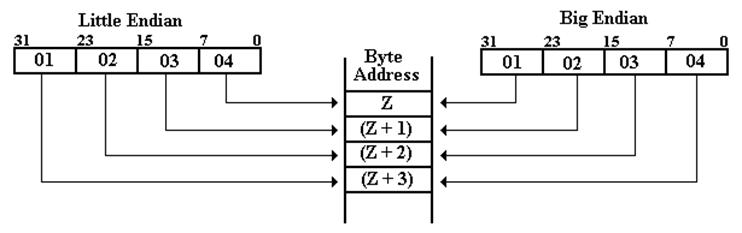
Example: “Core Dump” at Address 0x200

Note: Powers of 256 are 256⁰ = 1, 256¹ = 256,
256² = 65536, 256³ = 16,777,216

Suppose one has the following memory map as a result of a core dump.
The memory is byte addressable.

Address	0x200	0x201	0x202	0x203
Contents	02	04	06	08

What is the value of the 32–bit long integer stored at address 0x200?

This is stored in the four bytes at addresses 0x200, 0x201, 0x202, and 0x203.

Big Endian: The number is 0x02040608. Its decimal value is
2·256³ + 4·256² + 6·256¹ + 8·1 = 33,818,120

Little Endian: The number is 0x08060402. Its decimal value is
8·256³ + 6·256² + 4·256¹ + 2·1 = 134,611,970.

NOTE: Read the bytes backwards, not the hexadecimal digits.

Example 2: “Core Dump” at Address 0x200

Note: Powers of 256 are 256⁰ = 1, 256¹ = 256,
256² = 65536, 256³ = 16,777,216

Suppose one has the following memory map as a result of a core dump.
The memory is byte addressable.

Address	0x200	0x201	0x202	0x203
Contents	02	04	06	08

What is the value of the 16–bit integer stored at address 0x200?

This is stored in the two bytes at addresses 0x200 and 0x201.

Big Endian The value is 0x0204.
The decimal value is 2·256 + 4 = 516

Little Endian: The value is 0x0402.
The decimal value s 4·256 + 2 = 1,026

Note: The bytes at addresses 0x202 and 0x203 are not part of this
16–bit integer.

Design Problem: Fabricating a Memory from Chips

Here is an example of a design problem that I often like to assign. We shall
first discuss the terms and then solve the problem.

1. Suppose that a 8M by 32 main memory is built using
1M by 8 RAM chips and that memory is 32–bit word addressable.

a) How many RAM chips are necessary?

b) How many address bits are sent to each RAM chip?

c) How many address bits would be used to select the RAM chip?

d) Assuming low–order interleaving, which address bits will select the
RAM chip and which bits are sent to each RAM chip?

There are quite a few terms to define before we start the solution.

Design Problem: Specifying the Memory Size

In general, the term “M by N memory” refers to a memory with M entries,
each of N bits.

Recall that the term M, as in MB, usually refers to the number 2²⁰ = 1048576.
Thus, we have 8M = 8·2²⁰ = 2³·2²⁰ = 2²³.

The “8M by 32 main memory” has 2²³ addressable words, each being
32 bits in length. Each word contains four bytes.

This memory has 4·2²³ = 2²·2²³ = 2²⁵ bytes.

Each chip is described as “1M by 8”; each entry has 8 bits (1 byte).
The chip is a 1MB chip, holding 2²⁰ bytes.

Note that all common memory sizes are now quoted in bytes and are commonly
either a power of 2 or the sum of two powers of 2.

Examples: 128MB (byte count = 2²⁷), 384 MB (byte count = 2²⁸ + 2²⁷), etc.

The General Problem
and Its Constraints

The statement is always of the form “design a M₁ by N₁ memory using
chips of size M₂ by N₂.

Here are the constraints under which we shall design.

1. The size of an entry in the chip will always be a power of 2: N₂ = 2^K2.
Examples include: 1 bit, 2 bits, 4 bits, 8 bits (one byte), etc.

2. The number of words in a chip will almost always be a power of 2.
While it is possible to imagine a chip holding 384 bytes, this is rare.

In addition, we shall have some constraints on the relative sizes.

3. Either N₁ is an exact multiple of N₂ or N₂ is an exact multiple of N₁.
In math terms, either N₂ | N₁ (N₂ is a divisor of N₁) or N₁ | N₂.
This disallows monstrosities such as an 8K by 10 bit memory
to be built from 1K by 8 chips. Hint: This takes 16 chips.

4. M₁ and M₂ have a predictable relationship, which facilitates the design.
This relationship is hard to state exactly.

The Chip Count and the Bank Count

The memory will usually be divided into a number of banks, each containing
a number of chips that is usually a power of 2.

For well–behaved “non monstrous” cases, the chip count is easily computed,
as is the number of memory banks.

In the most common cases, the following hold.

1. The number of chips is just equal to (M₁·N₁) / (M₂·N₂).

2. The number of banks of memory is just equal to M₁ / M₂.
This obviously assumes that M₁ is a multiple of M₂.

3. The number of chips per memory bank is just equal to N₁ / N₂.
This obviously assumes that N₁ is a multiple of N₂.

The Original Problem

Suppose that a 8M by 32 main memory is built using
1M by 8 RAM chips and that memory is 32–bit word addressable.

1. The number of chips is (8·2²⁰ · 32) / (1·2²⁰ · 8) = (2²³·2⁵) / (2²⁰·2³) =
(2²⁸) / (2²³) = 2⁵ = 32.

2. The number of memory banks is (8·2²⁰) / (1·2²⁰) = 8

3. The number of chips per bank is 32 / 8 = 4.

Note that in this case, the product of the second and third calculation
is the result of the first calculation.

In this case, each chip contains 1M = 2²⁰ memory cells.
This necessitates 20 address lines to each chip.

There are 8 banks of chips, requiring 3 bits to select each bank.

The entire memory has 8M = 2²³ addressable words.
This necessitates 23 address bits.

The Organization into Memory Banks

Interleaved Memory

In this case, we need 23 bits to address the memory.
20 of these bits must be sent to every chip.

The most common arrangement is low–order interleaving,
often just called “interleaved memory”.

In this arrangement, the low–order bits select the bank,
and the other bits are sent to every bank.

Here we need three bits for the bank select.

This table shows the allocation of the 23 address bits A₂₂ – A₀.

To every bank	Bank select
Bits 22 – 3	Bits 2 – 0

Problem 2: Construct a 2K by 4 ROM

In this problem, we convert a 1K by 8 ROM into a 2K by 4 ROM.

This is cast as a Read–Only Memory to avoid a design issue
that is not central to this discussion.

Each of the two memories has 8Kb = 8,192 bits. The design is possible.

This design calls for an eleven–bit address: A₁₀ – A₀.

The 1K by 8 ROM requires a ten–bit address. In this design,
I use A₁₀ – A₁.

Each byte in the 1K by 8 ROM will hold two 4–bit cells
for the 2K by 4 ROM. Address bit A₀ will select.

If A₀ = 1, use bits 7 – 4 of the byte addressed by A₁₀ – A₁.

If A₀ = 0, use bits 3 – 0 of the byte addressed by A₁₀ – A₁.

Problem 2: Solution

Here is the solution. It uses four 2–to–1 multiplexers to produce the
four–bit memory output.

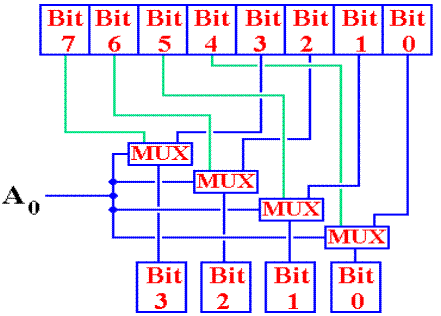
It is likely that this is not a design that one would see in a real–world
implementation. It is just an interesting academic problem.