Major and Minor States

We now consider the micro–operations and control signals associated
with the execution of each instruction in the ISA.

The execution of each instruction is divided into three phases.

These phases are called “major states”. They are:

1. Fetch: The instruction is fetched from memory.

2. Defer: This phase handles the computation of indirect addresses.

3. Execute: The instruction is executed and the result stored.

Each major state is broken into a number of minor states,
each with duration of one clock pulse.

In the hardwired control unit, each major state will comprise four minor states,
called T0, T1, T2, and T3.

This inflexible design is due to the simplicity of the control unit.

In the microprogrammed control unit, each of these major states is just suggestive,
corresponding to a section of the microcode.

Each state in the microcode takes as many clock pulses as necessary.

The Hardwired Control Unit: Basis for Design

As stated above, the hardwired control unit issues control signals based on:

1. The op–code in bits 31 – 27 of the IR (Instruction Register).

2. The ALU condition flags: N, Z, and C.

3. The Major State: one of Fetch, Defer, or Execute.

4. The Minor State: one of T0, T1, T2, or T3.

The 5–bit op–code is an input to a 5–to–32 decoder. Each of the outputs of this decoder
is associated with and labeled by an instruction in the ISA.

Boolean control signals emitted by this decoder are HLT, LDI, ANDI, ADDI, GET, PUT,
RET, RTI, LDR, STR, JSR, BR, LLS, LCS, RLS, RAS, NOT, ADD, SUB, AND, OR,
and XOR. Each of these corresponds to the related assembly language instruction.

Example: The assembly language instruction ADD has op–code 10101 (decimal 21).

When the input to the decoder is 10101, then the output Y₂₁ is activated.
This output is the Boolean control signal ADD; ADD = 1.

When ADD = 1, the op–code is that for the ADD instruction.

All other signals are Boolean and have value either 0 or 1. Thus we can say Fetch = 1
when the major state is Fetch, T2 = 1 when the minor state is T2, etc.

The Hardwired Control Unit: Sequencing the States

In the hardwired control unit, each of the major state and the minor state must progress
in a predictable sequence.

The minor state sequence is fixed and predictable; it is shown in the figure below.

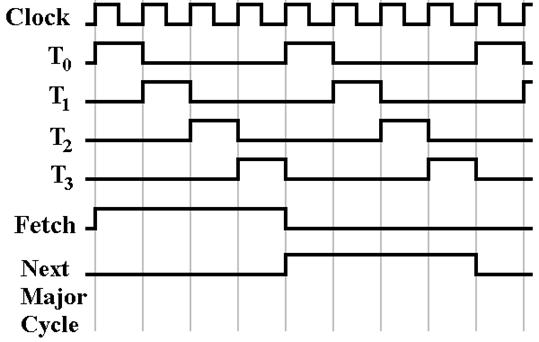
Here we see that each minor state is active for exactly the duration of one clock pulse.

The Minor State Register

Note that the minor state register continuously repeats the sequence T0, T1, T2, T3, etc.

It is a modulo–4 counter. Here is the implementation of the minor state register
as a “one hot” modulo–4 counter. The signal “Start” initializes the counter.

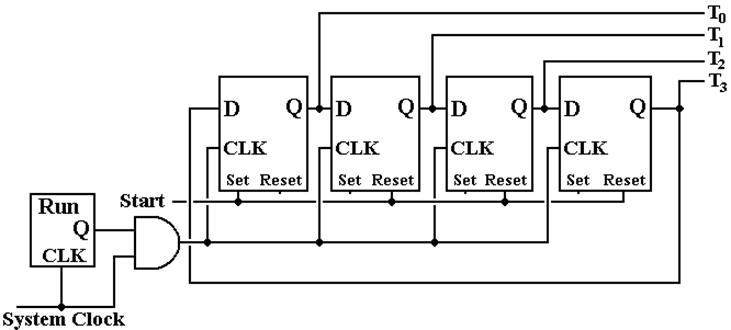
When the run flip–flop is set, the clock pulses get through to the state register
and cause it to count.

When the run flip–flop is reset (Q = 0), clock pulses are no longer fed to the counter
and the minor state becomes static.

Sequencing the Major State Register

The major state register might easily be considered a modulo–3 counter with values

00 Fetch denoted by “F” in these notes

01 Defer denoted by “D” in these notes

10 Execute denoted by “E” in these notes

In this design the major states move in sequence: F, D, E, F, D, E, F, D, E, etc.

This extremely simple design is very wasteful. Why spend four clock times in the Defer
state if the instruction does not use indirect addressing, the only reason for that state.

So we now consider modification of the minor state register so that

When indirect addressing is used, the state following Fetch is Defer

When indirect addressing is not used, the state following Fetch is not Defer.

Does this modification imply that the state following Fetch is either Defer or Execute
depending on whether or not indirect addressing is used?

This is not necessarily so. We have another trick up our sleeve.

The Common Fetch Sequence and Its Implications

Here is a slight restatement of the control signals for the common fetch sequence.

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)

F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1

F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)

F, T3: // Do something related to the instruction.

As we shall see, many of the instructions can be executed in one clock pulse.

We now ask ourselves the following question. If the execution of an instruction can be
completed in the Fetch phase, why enter the Execute phase and waste four clock cycles.

The answer is simple: there is no reason.

We now ask the first question about sequencing the major state register.
What state follows Fetch?

If the instruction execution can be completed in Fetch, the next state is Fetch.

If it cannot be completed in Fetch and indirect addressing used, the next state is Defer.

If it cannot be completed in Fetch and indirect addressing is not used,
the next state is Execute.

More on the Major State Register

What we have discovered is as follows.

1. The minor state register is a simple modulo–four counter.

As long as the computer is running, this counter continues to produce output.

The sequence is always the same: T0, T1, T2, T3, T0, T1, T2, T3, etc.

Note that each minor state is labeled by the control signal that is active.

T0: T0 = 1 T1 = 0 T2 = 0 T3 = 0

T1: T0 = 0 T1 = 1 T2 = 0 T3 = 0, etc.

2. The major state register is a modified modulo–three counter.

The sequence always begins with Fetch, but the next major state after
a given one depends on the instruction being executed.

Each major state has Boolean control signals associated.

Fetch: F = 1 D = 0 E = 0

Defer: F = 0 D = 1 E = 0

Execute: F = 0 D = 0 E = 1.

In order to design the major state register, we must first examine the sequence of
microoperations (and control signals) associated with each instruction in the ISA.

Top–Level View of the ALU

In our previous discussions, we have seen the need for the ALU to respond to the
following three control signals.

tra1 transfer the contents of bus B1 to bus B3.

tra2 transfer the contents of bus B2 to bus B3.

add add the contents of busses B1 and B2, place the sum on bus B3.

Examination of the register–to–register operations shows the necessity of additional
control signals to the ALU in order to execute the instructions.

shift needed by the shift operations LLS, LCS, RLS, RAS
The type of shift is determined by additional control signals

not needed by the logical not operation

sub needed by the subtraction operation

or needed by the logical OR operation

and needed by the logical AND operation

xor needed by the logical exclusive OR operation

Given this, let’s examine the control signals, beginning with the register operations.

Overview of Register–To–Register Operations

The structure of the Fetch phase of all register–to–register operations follows
a simple common pattern.

F, T0 – F, T2: This is the common fetch sequence.
All instructions share this part.

F, T3: Source register or source registers placed on the bus structure

Command the ALU with the appropriate control signal

Transfer bus B3 to the destination register.

For dyadic operations, we have SR2 ® B2 and SR1 ® B1.

For monadic operations, we have SR ® B2.

The ALU commands are one of those listed on the previous slide, but repeated here:

shift (with the shift type specified by control signals L/, A, and C)

not

add, sub, or, and, xor

Monadic Register–To–Register Operations (Part 1)

Each of these instructions can be executed in one clock pulse, so that
the execution is completed in the Fetch phase, with no Defer or Execute.

The type of shift is determined by three Boolean control signals.

L / : If L / = 0, this is a right shift. If L / = 1, it is a left shift.

A, C: If C = 1, this is a circular shift. The A flag is not used here.

If C = 0 and A = 1, this is an arithmetic shift.

If C = 0 and A = 0, this is a logical shift.

Note that a shift cannot be both circular and arithmetic.

This implies a convention for handling the case in which A = 1 and C = 1.

The fact that the control unit should never assert these two signals does not remove
the necessity for designing for this eventuality.

The design decision here is that the circular flag takes precedence, so that

C = 1, A = 0 this is a circular shift

C = 1, A = 1 this is also a circular shift

Monadic Register–To–Register Operations (Part 2)
Left Shifts

LLS Op-Code = 10000 (Hexadecimal 0x10)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B2, shift, L / = 1, A = 0. C = 0, B3 ® R.

LCS Op-Code = 10001 (Hexadecimal 0x11)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B2, shift, L / = 1, A = 0. C = 1, B3 ® R.

When we implement the shifter, we shall cause left arithmetic shifts to be
equivalent to left logical shifts, so that for left shifts we have the following:

C = 0 logical left shift (without regard to the value of the A flag).

C = 1 circular left shift (without regard to the value of the A flag).

Monadic Register–To–Register Operations (Part 3)
Right Shifts and Logical Negation

RLS Op-Code = 10010 (Hexadecimal 0x12)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B2, shift, L / = 0, A = 0. C = 0, B3 ® R.

RAS Op-Code = 10011 (Hexadecimal 0x13)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B2, shift, L / = 0, A = 1. C = 0, B3 ® R.

NOT Op-Code = 10100 (Hexadecimal 0x14)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B2, not, B3 ® R.

Dyadic Register–To–Register Operations
Arithmetic Operations

ADD Op-Code = 10101 (Hexadecimal 0x15)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B1, R ® B2, add, B3 ® R.

SUB Op-Code = 10110 (Hexadecimal 0x16)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B1, R ® B2, sub, B3 ® R.

Dyadic Register–To–Register Operations
Boolean Operations

AND Op-Code = 10111 (Hexadecimal 0x17)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B1, R ® B2, and, B3 ® R.

OR Op-Code = 11000 (Hexadecimal 0x18)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B1, R ® B2, or, B3 ® R.

XOR Op-Code = 11001 (Hexadecimal 0x19)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: R ® B1, R ® B2, xor, B3 ® R.

Immediate Mode Operations (Part 1)

HLT Op-Code = 00000 (Hexadecimal 0x00)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: 0 ® RUN. // Reset the RUN Flip-Flop

At this point, the sequencing of the major and minor states stops.

Memory and register contents are preserved for manual debugging.

The next state will be (F, T0) whenever the computer is restarted.

LDI Op-Code = 00001 (Hexadecimal 0x01)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, extend, tra1, B3 ® R. // Copy IR_19-0 as signed integer

Immediate Mode Operations (Part 2)

ANDI Op-Code = 00010 (Hexadecimal 0x02)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, and, B3 ® R. // Copy IR_19-0 as 20 bits.
// The 20 bits IR_19-0 are copied without extension, so we have in reality
// 0000 0000 0000 ¢ IR_19-0 ® B1. This may be changed in a future design.

ADDI Op-Code = 00011 (Hexadecimal 0x03)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, extend, add, B3 ® R. // Add signed integer

NOTE: Up to this point, every instruction examined can be executed in one clock

cycle following the three clock cycles needed to fetch it.

Fourteen of the twenty–two instructions can be so executed.

RISC Design: A Side Note

Let us imagine a standard Reduced Instruction Set Computer (RISC) design with a
well–functioning instruction prefetch unit.

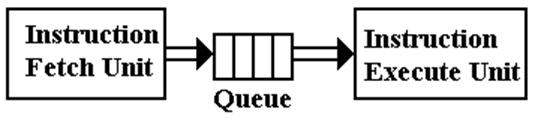
Here we assume that the prefetch unit maintains a queue of instructions that are ready
to be run by the execution unit and immediately available for transfer to the IR.

Under these circumstances, there is no fetch penalty for an instruction.

Put another way, the common fetch sequence discussed above goes away and
each of the previous fourteen instructions could be executed in one clock cycle total time.

Whenever one sees the design goal of one instruction executed per clock cycle in the
early RISC designs, it is this phenomenon that is being described.

Later superscalar designs, with multiple execution units, aim to execute multiple
instructions per clock cycle.

Instructions That Use the Execute Cycle

Here we note a division in the instruction set.

There are 14 instructions that can be executed in one clock cycle.
These can be completed in the Fetch phase.

The remaining 8 instructions require more than one clock cycle to
complete execution. These 8 must be extended into the Execute Cycle.

These eight that require “extra time” for execution are:

01000 GET Input into a general purpose register.

01001 PUT Output from a general purpose register.

01010 RET Return from subroutine.

01011 RTI Return from an interrupt handler.

01100 LDR Load general purpose register from memory.

01101 STR Store general purpose register into memory.

01110 JSR Call subroutine.

01111 BR Branch (Jump), either conditionally or unconditionally.

The fact that these instructions share the “01” prefix will be used later in
the design of the part of the control unit that sequences the major state register.

The Input and Output Instructions: Assumptions

At some point in the implementation of these two instructions, we must allow for the
fact that these two operations are basically asynchronous to the CPU.

To illustrate this point, consider two instructions STR and PUT.

STR store register to memory.

The memory timings are known and fixed. The microoperation sequence
that implements this instruction is designed to allow for the memory cycle time.

PUT copy register to an output device.

The timings for the output device are quite variable, and can appear random.

The microoperation sequence must depend on a signal from the output device
that it is ready to accept data; otherwise output data will be lost.

One way to handle this is to set up a “handshaking protocol” using one or more
D flip–flops to signal availability of data and readiness to transfer that data.

The Boz–5 design is based on device interrupts.

An input device interrupts when it has data ready for input.

An output device interrupts when it can accept more data.

This removes the complexity of the handshake.

The Input and Output Instructions: Implementation

For each of these two instructions, the design calls for execution that requires
two clock cycles. Neither can be completed within the Fetch phase.

Since completion in the Fetch phase is not possible, we remove all of the execution steps
to the Execute phase. This will simplify the control unit in that Fetch will be simpler.

We now ask ourselves how to place two microoperations into four time slots. Placement
into slots T0 and T2 is somewhat arbitrary, though less likely to cause difficulties.

GET Op-Code = 01000 (Hexadecimal 0x08)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: WAIT.

E, T0: IR ® B1, tra1, B3 ® IOA. // Send out the I/O address
E, T1: WAIT.
E, T2: IOD ® B2, tra2, B3 ® R. // Get the results.
E, T3: WAIT.

Again, note the assumption in (E, T2) that the input data has data ready to transfer.

Implementation of the Put Instruction

PUT Op-Code = 01001 (Hexadecimal 0x09)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: WAIT.

E, T0: R ® B2, tra2, B3 ® IOD // Get the data ready
E, T1: WAIT.
E, T2: IR ® B1, tra1, B3 ® IOA. // Sending out the address
E, T3: WAIT. // causes the output of data.

Here again, we assume that the output device can accept the data when it is sent out.

The control sequence in (E, T2) may be incomplete. Were this actually implemented,
we might discover the need for another control signal to affect the output.

Output causes the addressed output unit to copy the data from its
bus data register into its internal data registers.

NOTE: Neither GET nor PUT involve a memory address.

Three Instructions: JSR, RET, and RTI

We shall postpone the discussion of the subroutine–related instructions (JSR and RET)
until we have developed a strategy for subroutine linkage.

We mention in passing the difference between the two instructions RET and RTI.

At one level, the two instructions seem to be identical. Each involves a return from
a subprogram that was executed to achieve a specific purpose.

The main difference is due to the nature of an interrupt and depends on the details
of handling an interrupt.

It is possible to specify a structure in which interrupts are handled in the same way
as subroutine calls. In that case we do not need two return instructions.

On the Boz–5, the implementation of the RTI instruction is yet to be defined.

We specify two return instructions, RET and RTI, just to show that there might
be a difference.

Address Computation: Preconditions on the Execute Phase

We have four instructions that use an Effective Address in memory.

LDR Load a general–purpose register from the memory at the effective address.

STR Store a general–purpose register into memory at the effective address.

JSR Jump to the subroutine at the effective address.

BR Branch to the memory at the effective address.

What these instructions have in common is the use of an effective address.

We stipulate a simple precondition on the Execute Phase.
The Effective Address will be in the MAR (Memory Address Register).

This gives rise to a postcondition on the Fetch phase: it must leave an address in
the MAR.

Design of the Defer State: Preconditions and Postconditions

Due to the precondition on Execute, each of Fetch and Defer must
leave an address in the MAR.

Our scheme is based on two assumptions:

1. Pre–indexed addressing is used; indexing is done before indirection.

2. The Defer State handles only computation of indirect addressing.

These observations lead to conditions on both Fetch and Defer.

Fetch Postcondition A properly indexed address is placed into the MAR.

Defer Precondition The MAR holds an address.

Postcondition The MAR holds an address that correctly implements
the indirection.

If indirect addressing is not used,
the Fetch State computes the Effective Address based on proper indexing.

If indirect addressing is used,
the Defer State is used to compute the Effective Address,
based on the indexed address computed in Fetch.

Control Signals for the Defer State

The Defer State is entered for these four instructions when the I–bit is set.
The I–bit is IR₂₆.

The common “signature” of these four instructions is the prefix “011”.
When IR₃₁ = 0, IR₃₀ = 1, and IR₂₉ = 1, we have one of these four instructions.

The Defer State is entered from Fetch when IR₃₁ = 0, IR₃₀ = 1, IR₂₉ = 1, and IR₂₆ = 1.

Here are the control signals for Defer.

D, T0: READ. // Address is already in the MAR.
D, T1: WAIT. // Cannot access the MBR just now.
D, T2: MBR ® B2, tra2, B3 ® MAR. // MAR ¬ (MBR)
D, T3: WAIT. // Effective Address is now in the MAR.

Remember the precondition on the Defer State, which is the postcondition on Fetch.

The condition is that the properly indexed address is in the MAR.

If indirect addressing is used, then the MAR contains not the address of the argument,
but the address of a pointer to the argument. The memory at that address must be read
in order to obtain the address of the argument, which is then deposited into the MAR.

Control Signals for Load Register

Here is the complete set of control signals for LDR.

LDR Op-Code = 01100 (Hexadecimal 0x0C)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, add, B3 ® MAR. // Do the indexing.

Here the major state register takes control.
1) If the I–bit (bit 26) is 1, then the Defer state is entered.
2) If the I–bit is 0, then the E state is entered.

D, T0: READ. // Address is already in the MAR.
D, T1: WAIT. // Cannot access the MBR just now.
D, T2: MBR ® B2, tra2, B3 ® MAR. // MAR ¬ (MBR)
D, T3: WAIT.

The Execute state is entered either from Fetch or Defer.
E, T0: READ. // The Effective Address is in the MAR.
E, T1: WAIT. // Just read the memory at that address, wait,
E, T2: MBR ® B2, tra2, B3 ® R. // and then transfer its contents to the register.
E, T3: WAIT.

Control Signals for Store Register

Here is the complete set of control signals for STR.

STR Op-Code = 01101 (Hexadecimal 0x0D)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, add, B3 ® MAR. // Do the indexing.

D, T0: READ.
D, T1: WAIT.
D, T2: MBR ® B2, tra2, B3 ® MAR.
D, T3: WAIT.

E, T0: WAIT.
E, T1: R ® B1, tra1, B3 ® MBR, WRITE. // This could be in T0 or T2.
E, T2: WAIT. // Do not place the WRITE in T3
E, T3: WAIT. // we want it done by the end of T3.

In (E, T1) we send the contents of the source register to bus B1.

The reason given in the textbook is that bus B2 has been allocated for the index register.
However, the indexed addressing has already been computed; this allocation to B1 may
not be required. We shall just use it anyway as it causes no problems.

Conditional Branching: Use of the Major State Register

The branch instruction starts execution just as every other instruction that uses a
memory address and might use an indirect memory address.

Here is the complete fetch sequence for the BR instruction.

BR Op-Code = 01111 (Hexadecimal 0x0F)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, add, B3 ® MAR. // Do the indexing.

At the end of (F, T3) two things are known.

1. We have a conditional branch instruction.
Remember an unconditional branch is branch if 1 = 1, which always holds.

2. We have the values of the flags (N, Z, and C) from the previous operation,
so we know whether or not the branch will be taken.

If branch = 0, the state following Fetch is again Fetch.
The branch is not taken; the next instruction is fetched.

If branch = 1, the state following Fetch is either Defer or Execute; the branch is taken.

Control Signals for the Branch Instruction

BR Op-Code = 01111 (Hexadecimal 0x0F)

F, T0: PC ® B1, tra1, B3 ® MAR, READ. // MAR ¬ (PC)
F, T1: PC ® B1, 1 ® B2, add, B3 ® PC. // PC ¬ (PC) + 1
F, T2: MBR ® B2, tra2, B3 ® IR. // IR ¬ (MBR)
F, T3: IR ® B1, R ® B2, add, B3 ® MAR. // Do the indexing.

Here the Major State Register takes control. If the control signal Branch = 1, then the
following is executed. If the control signal Branch = 0, the next instruction is fetched.

D, T0: READ.
D, T1: WAIT.
D, T2: MBR ® B2, tra2, B3 ® MAR.
D, T3: WAIT.

E, T0: WAIT.
E, T1: WAIT.
E, T2: WAIT.
E, T3: MAR ® B1, tra1, B3 ® PC. // To jump, place a new address into the PC.