Multiprocessors, Multicomputers, and Clusters

In this and following lectures, we shall investigate a number of strategies for parallel computing, including a review of SIMD architectures but focusing on MIMD.

The two main classes of SIMD are vector processors and array processors.
We have already discussed each, but will mention them again just to be complete.

There are two main classes of MIMD architectures (Ref. 4, page 612):

a) Multiprocessors, which appear to have a shared memory and a
shared address space.

b) Multicomputers, which comprise a large number of independent processors
(each with its own memory) that communicate via a dedicated network.

Note that each of the SIMD and MIMD architectures call for multiple independent
processors. The main difference lies in the instruction stream.

SIMD architectures comprise a number of processors, each executing the same set of instructions (often in lock step).

MIMD architectures comprise a number of processors, each executing its own program.
It may be the case that a number are executing the same program; it is not required.

The Origin of Multicomputing

The basic multicomputing organization dates from the 19^th century, if not before.

The difference is that, before 1945, all computers were human; a “computer” was defined to be “a person who computes”. An office dedicated to computing employed dozens of human computers who would cooperate on solution of one large problem.

They used mechanical desk calculators to solve numeric equations, and paper as a medium of communication between the computers. Kathleen McNulty, an Irish immigrant, was one of the more famous computers. As she later described it:

“You do a multiplication and when the answer appeared, you had to write it down and reenter it. … To hand compute one trajectory took 30 to 40 hours.

This example, from the time of U.S. participation in the Second World War illustrates
the important features of multicomputing.

1. The problem was large, but could be broken into a large number
of independent pieces, each of which was rather small and manageable.

2. Each subproblem could be assigned to a single computer, with the expectation
that communication between independent computers would not occupy a
significant amount of the time devoted to solving the problem.

An Early Multicomputer

Here is a picture, probably from the 1940’s.

Note that each computer is quite busy working on a mechanical adding machine.

We may presume that computer–to–computer (interpersonal) communication was minimal and took place by passing data written on paper.

Note here that the computers appear all to be boys. Early experience indicated that grown men quickly became bored with the tasks and were not good computers.

Linear Speedup

Consider a computing system with N processors, possibly independent.

Let C(N) be the cost of the N–processor system, with C₁ = C(1) being the cost of one processor. Normally, we assume that C(N) » N·C₁, that the cost of the system
scales up approximately as fast as the number of processors.

Let P(N) be the performance of the N–processor system, measured in some conventional measure such as MFLOPS (Million Floating Operations Per Second), MIPS (Million Instructions per Second), or some similar terms.

Let P₁ = P(1) be the performance of a single processor system on the same measure.

The goal of any parallel processor system is linear speedup: P(N) » N·P₁. More properly, the actual goal is [P(N)/P₁] » [C(N)/C₁].

Define the speedup factor as S(N) = [P(N)/P₁]. The goal is S(N) » N.

Recall the pessimistic estimates from the early days of the supercomputer era that
for large values we have S(N) < [N / log₂(N)], which is not an encouraging number.

N	100	1000	10,000	100,000	1,000,000
Maximum S(N)	15	100	753	6,021	30,172

It may be that it was these values that slowed the development of parallel processors.

Amdahl’s Law

Here is a variant of Amdahl’s Law that addresses the speedup due to N processors.

Let T(N) be the time to execute the program on N processors, with
T₁ = T(1) be the time to execute the program on 1 processor.

The speedup factor is obviously S(N) = T(1) / T(N).

We consider any program as having two distinct components:
the code that can be sped up by parallel processing, and
the code that is essentially serialized.

Assume that the fraction of the code that can be sped up is denoted by variable X.

The time to execute the code on a single processor can be written as follows:

T(1) = X·T₁ + (1 – X)·T₁ = T₁

Amdahl’s Law states that the time on an N–processor system will be

T(N) = (X·T₁)/N + (1 – X)·T₁ = [(X/N) + (1 – X)]·T₁

The speedup is S(N) = T(1) / T(N) = =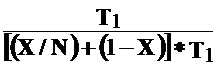

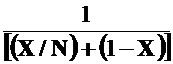
It is easy to show that S(N) = N if and only if X = 1.0; there is no part of the code that is essentially sequential in nature and cannot be run in parallel.

Some Results Due to Amdahl’s Law

Here are some results on speedup as a function of number of processors.

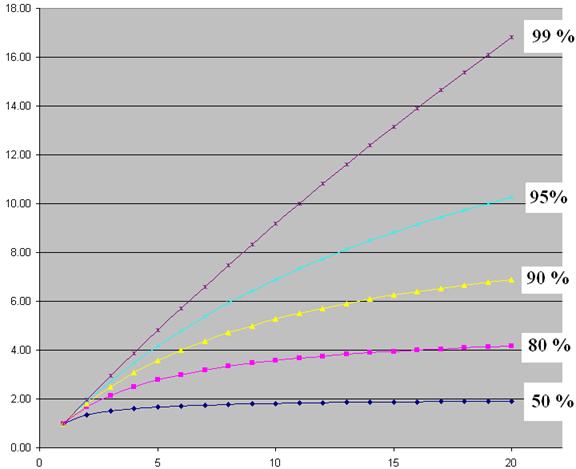
Note that even 5% purely sequential code really slows things down.

Overview of Parallel Processing

Early on, it was discovered that the design of a parallel processing system
is far from trivial if one wants reasonable performance.

In order to achieve reasonable performance, one must address a number of
important questions.

1. How do the parallel processors share data?

2. How do the parallel processors coordinate their computing schedules?

3. How many processors should be used?

4. What is the minimum speedup S(N) acceptable for N processors?
What are the factors that drive this decision?

In addition to the above question, there is the important one of matching the problem to the processing architecture. Put another way, the questions above must be answered
within the context of the problem to be solved.

For some hard real time problems (such as anti–aircraft defense), there might be a minimum speedup that needs to be achieved without regard to cost. Commercial problems rarely show this critical dependence on a specific performance level.

Sharing Data

There are two main categories here, each having subcategories.

Multiprocessors are computing systems in which all programs share a single address space. This may be achieved by use of a single memory or a collection of memory modules that are closely connected and addressable as a single unit.

All programs running on such a system communicate via shared variables in memory.

There are two major variants of multiprocessors: UMA and NUMA.

In UMA (Uniform Memory Access) multiprocessors, often called SMP (Symmetric Multiprocessors), each processor takes the same amount of time to access every
memory location. This property may be enforced by use of memory delays.

In NUMA (Non–Uniform Memory Access) multiprocessors, some memory accesses are faster than others. This model presents interesting challenges to the programmer in that race conditions become a real possibility, but offers increased performance.

Multicomputers are computing systems in which a collection of processors, each with its private memory, communicate via some dedicated network. Programs communicate by use of specific send message and receive message primitives.

There are 2 types of multicomputers: clusters and MPP (Massively Parallel Processors).

Coordination of Processes

Processes operating on parallel processors must be coordinated in order to insure
proper access to data and avoid the “lost update” problem associated with stale data.

In the stale data problem, a processor uses an old copy of a data item that has been updated. We must guarantee that each processor uses only “fresh data”.

Multiprocessors
One of the more common mechanisms for coordinating multiple processes in a single address space multiprocessor is called a lock. This feature is commonly used in
databases accessed by multiple users, even those implemented on single processors.

Multicomputers
These must use explicit synchronization messages in order to coordinate the processes. One method is called “barrier synchronization”, in which there are logical spots, called “barriers” in each of the programs. When a process reaches a barrier, it stops processing and waits until it has received a message allowing it to proceed.

The common idea is that each processor must wait at the barrier until every other processor has reached it. At that point every processor signals that it has reached the barrier and received the signal from every other processor. Then they all continue.

Classification of Parallel Processors

Here is a figure from Tanenbaum (Ref 4, page 588). It shows a taxonomy of parallel computers, including SIMD, MISD, and MIMD.

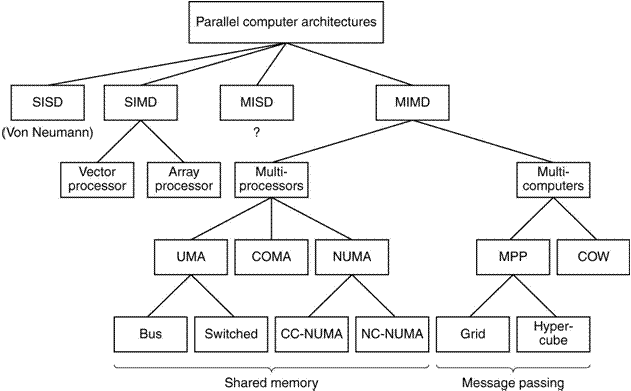
Note Tanenbaum’s sense of humor. What he elsewhere calls a cluster, he here calls a COW for Collection of Workstations.

Levels of Parallelism

Here is another figure from Tanenbaum (Ref. 4, page 549). It shows a number of levels of parallelism including multiprocessors and multicomputers.

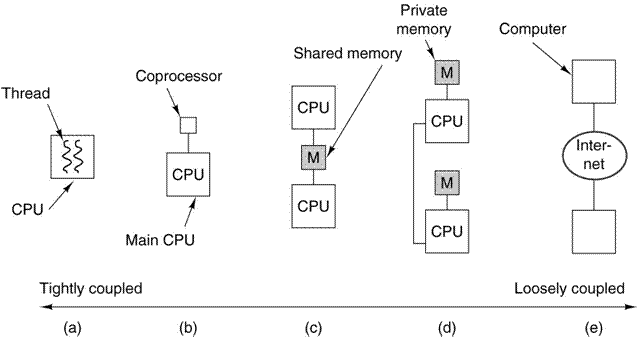
a) On–chip parallelism, b) An attached coprocessor (we shall discuss these soon),
c) A multiprocessor with shared memory, d) A multicomputer, each processor having
its private memory and cache, and e) A grid, which is a loosely coupled multicomputer.

Task Granularity

This is a model discussed by Harold Stone [Ref. 3, page 342]. It is formulated in terms of a time–sharing model of computation.

In time sharing, each process that is active on a computer is given a fixed time allocation, called a quantum, during which it can use the CPU. At the end of its quantum, it is timed out, and another process is given the CPU. The Operating System will move the place a reference to the timed–out process on a ready queue and restart it a bit later.

This model does not account for a process requesting I/O and not being able to use its entire quantum due to being blocked.

Let R be the length of the run–time quantum, measured in any convenient time unit.
Typical values are 10 to 100 milliseconds (0.01 to 0.10 seconds).

Let C be the amount of time during that run–time quantum that the process spends
in communication with other processes.

The applicable ratio is (R/C), which is defined only for 0 < C £ R.

In course–grain parallelism, R/C is fairly high so that computation is efficient.

In fine–grain parallelism, R/C is low and little work gets done due to the excessive overhead of communication and coordination among processors.

UMA Symmetric Multiprocessor Architectures

This is based on Section 9.3 of the text (Multiprocessors Connected by a Single Bus), except that I like the name UMA (Uniform Memory Access) better.

Beginning in the later 1980’s, it was discovered that several microprocessors can be usefully placed on a bus. We note immediately that, though the single–bus SMP architecture is easier to program, bus contention places an upper limit on the number of processors that can be attached. Even with use of cache memory for each processor to cut bus traffic, this upper limit seems to be about 32 processors (Ref 4. p 599).

Here, from Tanenbaum (Ref. 4, p. 594) is a depiction of three classes of bus–based UMA architectures: a) No caching, and two variants of individual processors with caches:
b) Just cache memory, and c) Both cache memory and a private memory.

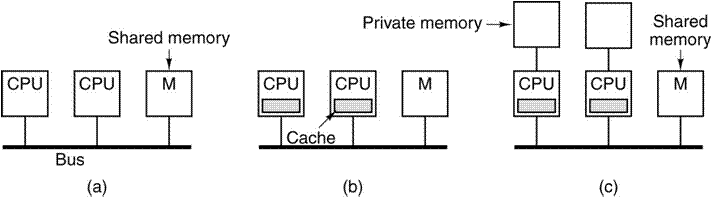
In each architecture, there is a global memory shared by all processors.

UMA: Other Connection Schemes

The bus structure is not the only way to connect a number of processors to a number of shared memories. Here are two others: the crossbar switch and the omega switch.

The Crossbar Switch

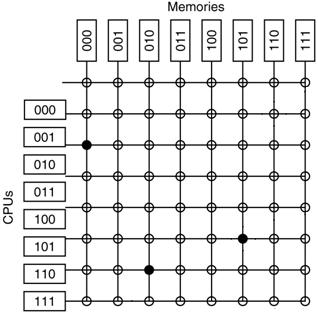
To attach N processors to M memories requires a crossbar switch with N·M switches. This is a non–blocking switch in that no processor will be denied access to a memory module due to the action of another processor. It is also quite expensive, as the number of switches essentially varies as the square of the number of connected components.

The Omega Switch

An Omega Switching Network routes packets of information between the processors and the memory units. It uses a number of 2–by–2 switches to achieve this goal.

Here is a three–state switching network. One can trace a path between any one processor and any one memory module. Note that this may be a blocking network.

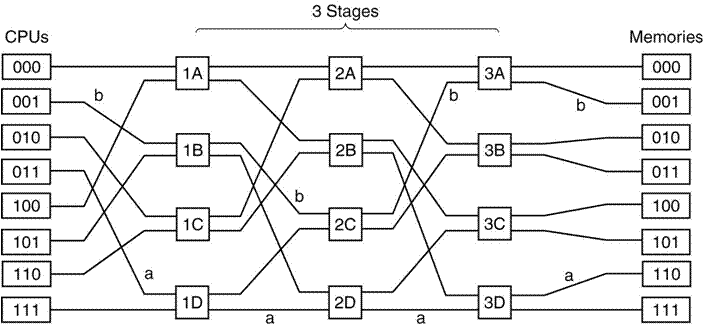
Cache Coherency

A big issue with the realization of the UMA multiprocessors was the development of protocols to maintain cache coherency. Briefly put, this insures that the value in any individual processor’s cache is the most current value and not stale data.

Ideally, each processor in a multiprocessor system will have its own “chunk of the problem”, referencing data that are not used by other processors. Cache coherency is not a problem in that case as the individual processors do not share data.

In real multiprocessor systems, there are data that must be shared between the individual processors. The amount of shared data is usually so large that a single bus would be overloaded were it not that each processor had its own cache.

When an individual processor accesses a block from the shared memory, that block is copied into that processors cache. There is no problem as long as the processor only reads the cache. As soon as the processor writes to the cache, we have a cache coherency problem. Other processors accessing those data might get stale copies.

One logical way to avoid this process is to implement each individual processor’s cache using the write–through strategy. In this strategy, the shared memory is updated as soon as the cache is updated. Naturally, this increases bus traffic significantly.

The next lecture will focus on strategies to maintain cache coherence.

References

In this lecture, material from one or more of the following references has been used.

1. Computer Organization and Design, David A. Patterson & John L. Hennessy,
Morgan Kaufmann, (3^rd Edition, Revised Printing) 2007, (The course textbook)
ISBN 978 – 0 – 12 – 370606 – 5.

2. Computer Architecture: A Quantitative Approach, John L. Hennessy and David A.
Patterson, Morgan Kauffman, 1990. There is a later edition.
ISBN 1 – 55860 – 069 – 8.

3. High–Performance Computer Architecture, Harold S. Stone,
Addison–Wesley (Third Edition), 1993. ISBN 0 – 201 – 52688 – 3.

4. Structured Computer Organization, Andrew S. Tanenbaum,
Pearson/Prentice–Hall (Fifth Edition), 2006. ISBN 0 – 13 – 148521 – 0