Motivations
for Multiprocessing
Recalling the history of the late 1980’s and early
1990’s, we note that
originally there was little enthusiasm for multiprocessing.
At that time, it was thought that the upper limit on
processor count in a
serious computer would be either 8 or 16.
In the 1990’s, experiments at
of multiprocessor systems with a few thousand commodity CPUs.
As of early 2010, the champion processor was the
Jaguar, a Cray XT5.
It had a peak performance of 2.5 petaflops (2.5·1015 floating point operations
per second) and a sustained performance in excess of 1.0 petaflop.
The Jaguar comprises 66,247 quad–core AMD Opteron
processors, uses
12.7 megawatts of electric power, and requires a supply of both chilled water
(6,800 gallons/minute at 42° F) and considerable chilled air.
Multicore processors arose in response to another
challenge: the “power wall”.
Current multicore processors have 8 to 16 cores on a single chip, in an attempt
to get more work for less electrical power.
The Focus
for Multiprocessing
Multiprocessing is designed and intended to facilitate
parallel processing.
Remember that there are several classes of
parallelism, only one of which
presents a significant challenge to the computer system designer.
Job–level
parallelism or process–level parallelism uses multiple processors
to run multiple independent programs simultaneously. As these programs do
not communicate with each other, the design of systems to support this class
of programs presents very little challenge.
The true challenge arises with what might be called a parallel processing
program, in which a single program executes on multiple processors. In this
definition is the assumption that there must be some interdependencies between
the multiple execution units.
In this set of lectures, we shall focus on designs for
efficient execution of
solutions to large single software problems, such as weather forecasting,
fluid flow modeling, and so on.
A Warning
from Mr. Amdahl
Recall Amdahl’s law, which is a generalization of a
simple observation about
the nature of code in which only a certain fraction (0.0 £ F £ 1.0) can be
executed in parallel.
The maximum speed–up for a collection of N processors
is given by one
variant of Amdahl’s Law.
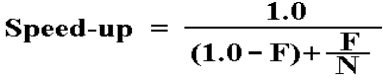
Note that this law directly implies a maximum speed–up
that is a function
only of the fraction of code that can be run in parallel.
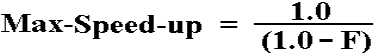
So, if only 99% of the code can be run in parallel,
then the maximum
speed–up is 100 independently of the number of processors.
Amdahl’s
Law: Good News and Bad News
Before we get too worried about an apparently gloomy
prediction, we must
understand that Amdahl’s Law is based on count of statements executed.
Consider the following program fragment, which we
shall pretend is complete.
For J = 1 to 1000 Do
For K = 1 to 1000 Do
A[J][K]
= 0 ; // Or A(J,K) = 0, if you like.
This fragment appears to have only three executable
lines of code.
However, the loop structure represents one million
executable statements.
If each is done in parallel at the same time, we have a speed–up of one
million.
However, consider the following fragment.
For J = 1 to 10 Do
For K = 1 to 10 Do
A[J][K]
= 0 ; // Or A(J,K) = 0, if you like.
The maximum speed–up here will be 100, because there
is nothing for
any additional processors to do.
The
Challenge for Multiprocessors
As multicore processors evolve into manycore
processors (with a few hundreds
of cores), the challenge remains the same as it always has been.
The goal is to get an increase in computing power (or
performance or whatever)
that is proportional to the cost of providing a large number of processors.
The design problems associated with multicore
processors remain the same
as they have always been: how to coordinate the work of a large number of
computing units so that each is doing useful work.
These problems generally do not arise when the
computer is processing a
number of independent jobs that do not need to communicate.
The main part of these design problems is management
of access to shared
memory. This part has two aspects:
1. The cache coherency problem, discussed
earlier.
2. The problem of process synchronization,
requiring the use of lock
variables, and reliable processes
to lock and unlock these variables.
A Naive Lock
Mechanism and Its Problems
Consider a shared memory variable, called LOCK, used to control
access
to a specific shared resource. This
simple variable has two values:
When the
variable has value 0, the lock is free and a process may
set the lock value to 1 and obtain the
resource.
When the
variable has value 1, the lock is unavailable and any
process must wait to have access to the
resource.
Here is the simplistic code (written in Boz–5 assembly
language) that is
executed by any process to access the variable.
GETIT LDR %R1,LOCK LOAD THE LOCK
VALUE INTO R1.
CMP %R1,%R0 IS THE VALUE
0?
REGISTER R0 IS
IDENTICALLY 0.
BGT GETIT NO, IT IS 1. TRY AGAIN.
LDI %R1,1 SET THE
REGISTER TO VALUE 1
STR %R1,LOCK STORE VALUE
OF 1, LOCKING IT
The Obvious
Problem
Event Process 1 Process 2
LOCK = 0
LDR %R1,LOCK
%R1 has value 0
CMP %R1,%R0
Compares OK. Continue
Context switch LDR %R1,LOCK
%R1 has value 0
Set LOCK = 1
Continue
LOCK = 1
Context switch LDI %R1,1
STR %R1,LOCK
Continue
LOCK = 1
Each process has access to the resource and continues
processing.
Atomic
Synchronization Primitives
What is needed is an atomic operation, defined in the
original sense of the
word to be an operation that must complete once it begins. Specifically it
cannot be interrupted or suspended by a context switch.
There may be some problems associated with virtual
memory, particularly
arising from page faults. These are
easily fixed.
We consider an atomic instruction that is to be called
CAS, standing for either:
Compare and
Set, or
Compare and
Swap
Either of these takes three arguments: a lock
variable, an expected value
(allowing the resource to be accessed) and an updated value (blocking access
by other processes to this resource).
Here is a sample of proper use.
LDR %R1,LOCK ATTEMPT
ACCESS, POSSIBLY
CAUSING A PAGE
FAULT
CAS LOCK,0,1 SET TO 1 TO
LOCK IT.
Two Variants
of CAS
Each variant is atomic; it is guaranteed to execute
with no interrupts or
context switches. It is a single CPU
instruction, directly executed by
the hardware.
Compare_and_set (X, expected_value, updated_value)
If (X == expected_value)
X ¬ updated_value
Return True
Else Return False
Compare_and_swap (X, expected_value, updated_value)
If (X == expected_value)
Swap X « updated_value
Return True
Else Return False
Such instructions date back at least to the IBM System/370
in 1970.
What About MESI?
Consider two processes executing on different
processors, each with its own
cache memory (probably both L1 and L2).
Let these processes be called P1 and P2. Suppose that each P1 and P2 have
the variable LOCK in cache memory and that each wants to set it.
Suppose P1 sets the lock first. This write to the cache block causes a
cache invalidate to be broadcast to
all other processes.
The shared memory value of LOCK is updated and then copied to the cache
associated with process P2.
However, there is no signal to P2 that the value in
its local registers has
become invalid. P2 will just write a new
value to its cache.
In other words, the MESI protocol will maintain the
integrity of values in
shared memory. However, it cannot be
used as a lock mechanism.
Any synchronization primitives that we design will
assume that the MESI
protocol is functioning properly and add important functionality to it.
CAS:
Implementation Problems
The single atomic CAS presents some problems in processor
design, as it
requires both a memory read and memory write in a single uninterruptable
instruction.
The option chosen by the designers of the MIPS is to
create a pair of
instructions in which the second instruction returns a value showing whether
or not the two executed as if they were atomic.
In the MIPS design, this pair of
instructions are as follows:
LL Load Linked LL Register, Memory Address
SC Store Conditional SC Register, Memory Address
This code either fails or swaps the value in register $S4 with the value in
the memory location with address in register $S1.
TRY: ADD $T0,$0,$S4 MOVE VALUE IN $S4 TO REGISTER $T0
LL $T1,0($S1) LOAD $T1 FROM MEMORY ADDRESS
SC $T0,0($S1) STORE CONDITIONAL
BEQ $T0,$0,TRY BRANCH STORE FAILS, GO BACK
ADD $S4,$0,$T1 PUT VALUE
INTO $S4
More on the
MESI Issue
Basically the MESI protocol presents an efficient
mechanism to handle the
effects of processor writes to shared memory.
MESI assumes a shared memory in which each addressable
item has a unique
memory address and hence a unique memory block number.
But note that the problem associated with MESI would
largely go away if we
could make one additional stipulation: once a block in shared memory is written
by a processor, only that processor will access that block for some time.
We shall see that a number of problems have this
desirable property.
We may assign multiple processors to the problem and enforce the following.
a) Each memory block can be read by any number of
processors,
provided that it is only
read.
b) Once a memory block is written to by one
processor, it is the
“sole property” of that
processor. No other processor may read
or write that memory block.
Remember that a processor accesses a memory block
through its copy in cache.
Sample
Problem: 2–D Matrix Multiplication
Here we consider the multiplication of two square
matrices, each of
size N–by–N, having row and column indices in the
range [0, N – 1].
The following is code such as one might see in a
typical serial implementation
to multiply square matrix A by square matrix B, producing square matrix C.
For I = 0 to (N – 1) Do
For J = 0 to (N – 1)
Do
Sum = 0 ;
For K = 0 to (N –
1) Do
SUM = SUM + A[I][K]·B[K][J] ;
End For
C[I][J]
= SUM ;
End For
End For
Note the use of SUM to avoid multiple references to C[I][J].
Memory
Organization of 2–D Arrays
Theoretically, the computation of any number of matrix
functions of two
square N–by–N matrices can be done very efficiently in parallel by an array
of N2 processors; each computing the results for one element in the
result array.
Doing this efficiently means that we must reduce all
arrays to one dimension, in
the way that the run–time support systems for high–level languages do.
Two–dimensional arrays make for good examples of this
in that they represent
the simplest data structures in which this effect is seen.
Multiply dimensioned arrays are stored in one of two
fashions: row major order
and column major order. Consider a
2–by–3 array X.
In row major order, the rows are stored contiguously.
X[0][0], X[0][1], X[0][2], X[1][0], X[1][1], X[1][0]
Most high–level languages use row major ordering.
In column major order, the columns are stored
contiguously
X[0][0], X[1][0], X[0][1], X[1][1], X[0][2], X[1][2]
Old FORTRAN is column major.
Sample
Allocations of Square Arrays to Memory
This example supposes a 4–by–4 array of double
precision real numbers.
Each number requires 8 bytes for storage, so that each row and each column
require 32 bytes. We are assuming a
cache block size of 32 bytes.
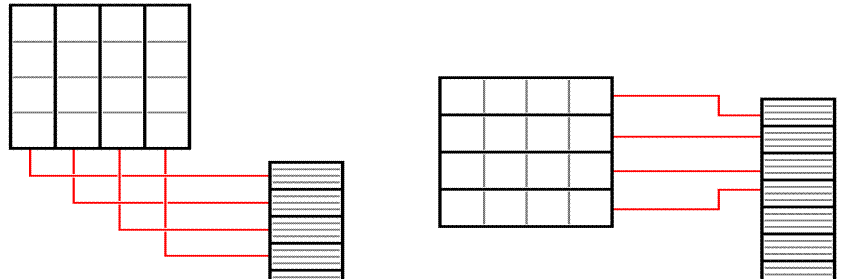
Column
Major Order Row
Major Order
If the array is stored in column major order and
accessed that way, we have at
most one page fault per column access.
This is due to the artificial constraint
that a column exactly fits a cache block.
Row major order behaves similarly.
Sample
Problem Code Rewritten
The following is code shows the one–dimensional access
to the 2–dimensional
arrays A, B, C. Each has row and column
indices in the range [0, N – 1].
For I = 0 to (N – 1) Do
For J = 0 to (N – 1)
Do
Sum = 0 ;
For K = 0 to (N –
1) Do
SUM = SUM + A[I·N + K]·B[K·N + J] ;
End For
C[I·N + J] = SUM ;
End For
End For
Note the use of SUM to avoid multiple references to C[I][J].
Some Issues
of Efficiency
The first issue is rather obvious and has been
assumed.
We might have written the code as follows.
For K = 0 to (N –
1) Do
C[I·N + J] = C[I·N + J] + A[I·N + K]·B[K·N + J] ;
End For
But note that this apparently simpler construct leads
to 2·N references to array
element C[I·N + J] for each value of I and J.
Array references are expensive, because the compiler
must generate code that
will allow access to any element in the array.
Our code has one reference to C[I·N + J] for each value
of I and J.
Sum = 0 ;
For K = 0 to (N –
1) Do
SUM = SUM + A[I·N + K]·B[K·N + J] ;
End For
C[I·N + J] = SUM ;
Array
Access: Another Efficiency Issue
In this discussion, we have evolved the key code
statement as follows.
We began with SUM = SUM + A[J][L]·B[L][K] ;
and changed to SUM = SUM +
A[I·N + K]·B[K·N + J] ;
The purpose of this evolution was to make explicit the
mechanism by which
the address of an element in a two–dimensional array is determined.
This one–dimensional access code exposes a major
inefficiency that is due to
the necessity of multiplication to determine the addresses of each of the two
array elements in this statement.
Compared to addition, multiplication is a very
time–consuming operation.
As written the key statement SUM = SUM + A[I·N + K]·B[K·N + J]
contains three multiplications, only one of which is essential to the code.
We now exchange the multiplication statements in the
address computations
for addition statements, which execute much more quickly.
Addition to
Generate Addresses in a
Change the inner loop to define and use the indices L and M as follows.
For K = 0 to (N –
1) Do
L = I·N + K ;
M = K·N + J ;
SUM = SUM + A[L]·B[M] ;
End For
Watch the values of L and M as
For K = 0 L = I·N M = J
For K = 1 L = I·N + 1 M = J + N
For K = 2 L = I·N + 2 M = J + 2·N
For K = 3 L = I·N + 3 M = J + 3·N
The Next
Evolution of the Code
This example eliminates all but one of the unnecessary
multiplications.
For I = 0 to (N – 1) Do
For J = 0 to (N – 1)
Do
Sum = 0 ;
L = I·N ;
M = J
;
For K = 0 to (N –
1) Do
SUM = SUM + A[L]·B[M] ;
L = L + 1 ;
M = M + N ;
End For
C[I·N + J] = SUM ;
End For
End For
It is considerations such as these that make for
efficient parallel execution.
Suppose a
Square Array of Processors
Suppose an array of N2 processors, one for
each element in the product array C.
Each of these processors will be assigned a unique row
and column pair.
Assume that process (I, J) is running on processor (I,
J) and that there
is a global mechanism for communicating these indices to each process.
Sum = 0 ;
L = I·N ;
M = J ;
INJ = L + M ; // Note we have I·N + J computed here.
For K = 0 to (N –
1) Do
SUM = SUM + A[L]·B[M] ;
L = L + 1 ;
M = M + N ;
End For
C[INJ]
= SUM ;
For large values of N, there is a significant speedup
to be realized.
Flynn’s
Taxonomy Revisited
A taxonomy is just a way of organizing items that are to be
studied.
Here is a taxonomy developed by Michael Flynn, who published it in 1966.
|
|
|
Data Streams |
|
|
|
|
Single |
Multiple |
|
Instruction |
Single |
SISD (Standard computer) |
SIMD (SSE on x86) |
|
Multiple |
MISD (No examples) |
MIMD (Parallel processing) |
|
This taxonomy is still taught today, as it continues to be useful in
characterizing
and analyzing computer architectures.
However, this taxonomy has been replaced for serious design use because
there
are too many interesting cases that cannot be exactly fit into one of its
classes.
Note that it is very likely that Flynn included the
MISD class just to be
complete. There is no evidence that a
viable MISD computer was ever
put to any real work.
Vector
computers form the most interesting
realization of SIMD architectures.
This is especially true for the latest incarnation, called CUDA.
SIMD vs.
SPMD
Actually, CUDA machines such as the NVIDIA GeForce
8800 represent
SPMD architectures and not SIMD architectures.
The difference between SIMD and SPMD is slight but
important.
The original SIMD architectures focused on amortizing
the cost of a control
unit over a number of processors by having a single CU control them all.
This is parallel program execution in which all
execution units respond to
a single instruction that is associated with a single PC (Program Counter).
Each execution unit has its own general purpose
registers and allocation of
shared memory, so SIMD does support multiple independent data streams.
This works very well on looping program structures,
but poorly in logic
statements, such as if..then..else, case, or switch.
SIMD:
Processing the “If statement”
Consider the following block of code, to be executed
on four processors
being run in SIMD mode. These are P0,
P1, P2, and P3.
if
(x > 0) then
y = y + 2 ;
else
y = y – 3;
Suppose that the x values are as follows (1, –3, 2, –4). Here is what
happens.
|
Instruction |
P0 |
P1 |
P2 |
P3 |
|
y = y + 2 |
y = y + 2 |
Nothing |
y = y + 2 |
Nothing |
|
y = y – 3 |
Nothing |
y = y – 3 |
Nothing |
y = y – 3 |
Execution units with data that do not fit the condition are disabled so
that units
with proper data may continue. This
causes inefficiencies.
What one wants to happen is possibly realized by the SPMD architecture.
|
P0 |
P1 |
P2 |
P3 |
|
y = y + 2 |
y = y – 3 |
y = y + 2 |
y = y – 3 |
SIMD vs.
SPMD vs. MIMD
The following figure illustrates the main difference
between the SIMD and
SPMD architectures and compares each to the MIMD architecture.
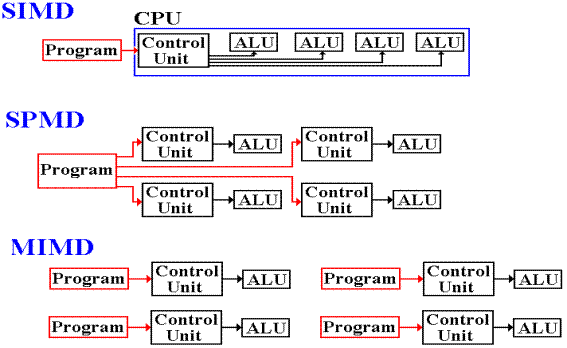
In a way, SPMD is equivalent to MIMD in which each
processor is running
the same high–level program. This does
not imply running the exact same
instruction stream, as data conditionals may differ between processors.
Another Look
at the NVIDIA GeForce 8800 GTX
Here, your author presents a few random thoughts about
this device.
As noted in the textbook, a “fully loaded” device has
16 multiprocessors, each
of which contains 8 streaming processors operating at 1.35 GHz.
Each streaming processor has a local memory with
capacity of 16 KB, along
with 8,192 (213) 32–bit registers.
The work load for computing is broken into threads,
with a thread block being
defined as a number of intercommunicating threads that must execute on the
same streaming processor. A block can
have up to 512 (29) threads.
Conjecture: This division
allows for sixteen 32–bit registers per thread.
Fact: The maximum performance of this device is 345.6 GFLOPS
(billion floating
point operations per second)
On
4/17/2010, the list price was $1320 per unit, which was
discounted to $200
per unit on Amazon.com.
Fact: In
1995, the fastest vector computer was a Cray T932. Its
maximum performance
was just under 60 GFLOPS.
It cost $39 million.